The SPP Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Testing Covariate Dependency with EDF Tests
In a test for covariate dependency, the goal is to test the null hypothesis  that the point process is independent of the covariate. PROC SPP tests
that the point process is independent of the covariate. PROC SPP tests  by interpolating the covariate values at the event locations. The EDF is weighted by the intensity at the corresponding locations
(Baddeley and Turner 2005). PROC SPP performs this weighted EDF test for covariates that are defined in a TREND
statement.
by interpolating the covariate values at the event locations. The EDF is weighted by the intensity at the corresponding locations
(Baddeley and Turner 2005). PROC SPP performs this weighted EDF test for covariates that are defined in a TREND
statement.
Weighted EDF Tests
To test dependence on a trend covariate, PROC SPP initially computes the covariate EDF. The EDF is weighted by using intensity-based
weights to account for the current intensity model. For example, under the CSR assumption the intensity 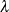 is constant across the study area; hence, the weight for each of the M observations of a covariate is
is constant across the study area; hence, the weight for each of the M observations of a covariate is 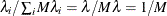 . This weighted EDF is the predicted distribution that any other set of independent covariate observations should follow under
the assumed intensity model.
. This weighted EDF is the predicted distribution that any other set of independent covariate observations should follow under
the assumed intensity model.
Next, the covariate is interpolated at the n event locations 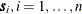 , using ordinary kriging; kriging analysis assumes a linear semivariance correlation function and considers the four closest
covariate observations for each event location. The outcome is a set of covariate values
, using ordinary kriging; kriging analysis assumes a linear semivariance correlation function and considers the four closest
covariate observations for each event location. The outcome is a set of covariate values 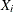 . With the
. With the 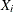 in hand, PROC SPP assumes that the probability integral transform
in hand, PROC SPP assumes that the probability integral transform 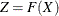 is the linear interpolation of the weighted EDF at the covariate values
is the linear interpolation of the weighted EDF at the covariate values 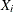 , and it produces the transformed EDF Z in
, and it produces the transformed EDF Z in ![$[0,1]$](images/statug_spp0148.png) . If the intensity model assumption is correct, then Z follows a uniform distribution
. If the intensity model assumption is correct, then Z follows a uniform distribution 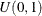 . Finally, PROC SPP uses EDF tests to examine the fit of the EDF
. Finally, PROC SPP uses EDF tests to examine the fit of the EDF 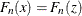 to a standard uniform EDF.
to a standard uniform EDF.