The SPP Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
EDF Goodness-of-Fit Tests
You use goodness-of-fit tests to examine the fit of a parametric distribution. In the SPP procedure, this task emerges when
you test your data for dependence on a covariate. You can examine the goodness of fit by using tests that are based on the
EDF. These tests offer advantages over traditional chi-square goodness-of-fit tests, as discussed in D’Agostino and Stephens
(1986). The empirical distribution function is defined for a set of n independent observations, 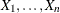 , that have a common distribution function
, that have a common distribution function 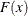 as follows. Denote the observations ordered from smallest to largest as
as follows. Denote the observations ordered from smallest to largest as 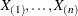 . Then the empirical distribution function,
. Then the empirical distribution function, 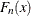 , is
, is
![\[ F_ n(x) = \left\{ \begin{array}{llr} 0, & x < X_{(1)} & \\[0.02in] \frac{i}{n}, & X_{(i)} \leq x < X_{(i+1)} & i=1,\ldots ,n-1 \\[0.02in] 1, & X_{(n)} \leq x & \end{array} \right. \]](images/statug_spp0126.png)
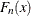 is a step function that takes a step of height
is a step function that takes a step of height 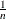 at each observation. This function estimates the distribution function
at each observation. This function estimates the distribution function 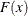 . At any value x,
. At any value x, 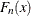 is the proportion of observations that are less than or equal to x, whereas
is the proportion of observations that are less than or equal to x, whereas 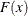 is the probability of an observation being less than or equal to x. EDF statistics measure the discrepancy between
is the probability of an observation being less than or equal to x. EDF statistics measure the discrepancy between 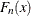 and
and 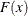 .
.
The computational formulas for the EDF statistics make use of the probability integral transformation 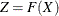 . If
. If 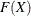 is the true distribution function of X, then the random variable Z is uniformly distributed between 0 and 1. For example, assume that you believe
is the true distribution function of X, then the random variable Z is uniformly distributed between 0 and 1. For example, assume that you believe 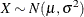 . In this case, the probability integral transform
. In this case, the probability integral transform 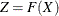 for the normal
for the normal 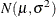 is given by the EDF of the standardized value
is given by the EDF of the standardized value 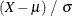 . To test the fit of your sample EDF
. To test the fit of your sample EDF 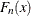 to the assumed exact
to the assumed exact 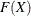 , you can equivalently test the fit of
, you can equivalently test the fit of 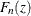 to the EDF
to the EDF 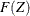 of Z. As
of Z. As 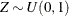 ,
, 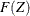 is the cumulative density function (CDF) of the standard uniform
is the cumulative density function (CDF) of the standard uniform 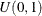 , which is simply
, which is simply 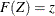 . This also means that your empirical
. This also means that your empirical 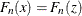 . Consequently, the probability integral transform translates the initial fit task into an easier comparison between
. Consequently, the probability integral transform translates the initial fit task into an easier comparison between 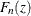 and
and 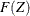 .
.
There are two main classes of EDF statistics: the supremum and the quadratic class. The supremum class is based on the largest
vertical difference between 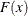 and
and 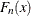 . The quadratic class is based on the squared difference
. The quadratic class is based on the squared difference 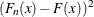 . Quadratic statistics have the following general form:
. Quadratic statistics have the following general form:
![\[ Q = n \int _{-\infty }^{+\infty } (F_ n(x)-F(x))^2 \psi (x) dF(x) \]](images/statug_spp0140.png)
The function 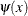 weights the squared difference
weights the squared difference 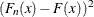 .
.
As previously discussed, the SPP procedure considers the ordered observations 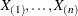 and computes the values
and computes the values 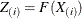 by applying the probability integral transform. PROC SPP examines the goodness of fit by computing the following two EDF
statistics:
by applying the probability integral transform. PROC SPP examines the goodness of fit by computing the following two EDF
statistics:
-
Kolmogorov-Smirnov two-sided D from the supremum class
-
Cramér-von Mises
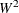 from the quadratic class
from the quadratic class
Within the different classes of EDF statistics, the quadratic class is known to have more powerful statistics than the supremum class. The details of the statistics used by PROC SPP are discussed in the following subsection.
After the EDF test statistics are computed, the SPP procedure computes the associated significance values. In the scope of
the PROC SPP analysis, the true distribution function, 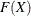 , is a completely specified distribution. For computations in this scenario, PROC SPP applies slightly modified D and
, is a completely specified distribution. For computations in this scenario, PROC SPP applies slightly modified D and 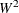 statistics, as described by D’Agostino and Stephens (1986).
statistics, as described by D’Agostino and Stephens (1986).