Example 26.29 Second-Order Confirmatory Factor Analysis
A second-order confirmatory factor analysis model is applied to a correlation matrix of Thurstone reported by McDonald (1985). The data set is shown in the following DATA step:
data Thurst(TYPE=CORR);
title "Example of THURSTONE resp. McDONALD (1985, p.57, p.105)";
_TYPE_ = 'CORR'; Input _NAME_ $ Obs1-Obs9;
label obs1='Sentences' obs2='Vocabulary' obs3='Sentence Completion'
obs4='First Letters' obs5='Four-letter Words' obs6='Suffices'
obs7='Letter series' obs8='Pedigrees' obs9='Letter Grouping';
datalines;
obs1 1. . . . . . . . .
obs2 .828 1. . . . . . . .
obs3 .776 .779 1. . . . . . .
obs4 .439 .493 .460 1. . . . . .
obs5 .432 .464 .425 .674 1. . . . .
obs6 .447 .489 .443 .590 .541 1. . . .
obs7 .447 .432 .401 .381 .402 .288 1. . .
obs8 .541 .537 .534 .350 .367 .320 .555 1. .
obs9 .380 .358 .359 .424 .446 .325 .598 .452 1.
;
Using the LINEQS modeling language, you specify the three-term second-order factor analysis model in the following statements:
proc calis data=Thurst nobs=213 corr nose;
lineqs
obs1 = x1 * f1 + e1,
obs2 = x2 * f1 + e2,
obs3 = x3 * f1 + e3,
obs4 = x4 * f2 + e4,
obs5 = x5 * f2 + e5,
obs6 = x6 * f2 + e6,
obs7 = x7 * f3 + e7,
obs8 = x8 * f3 + e8,
obs9 = x9 * f3 + e9,
f1 = x10 * f4 + e10,
f2 = x11 * f4 + e11,
f3 = x12 * f4 + e12;
variance
f4 = 1.,
e1-e9 = u1-u9,
e10-e12 = 3 * 1.;
bounds
0. <= u1-u9;
run;
In the PROC CALIS statement, you specify the data set in the DATA= option and the number of observations in the NOBS= option. With the CORR option, you request the correlations be analyzed. You use the NOSE option to suppress the computation of standard error estimates.
In the LINEQS statement, the first-order loadings for the three factors, f1, f2, and f3, each refer to three variables, X1-X3, X4-X6, and X7-X9, respectively. One second-order factor, f4, reflects the correlations among the three first-order factors, f1, f2, and f3.
In the VARIANCE statement, you fix the variance of f4 to 1.0 for identification. The variances of error terms e1–e9 are free parameters u1–u9. The error variances for the three first-order factors are also fixed at 1.0 for identification purposes.
You also specify the boundary constraints for the error variance parameters u1–u9. You require them to be positive in the estimation.
Output 26.29.1 shows the estimation results.
Output 26.29.1
Estimation Results of the Second-Order Factor Model for Thurstone Data: LINEQS Model
| Obs1 |
= |
|
0.5151 |
* |
f1 |
+ |
1.0000 |
|
e1 |
| |
|
|
|
|
x1 |
|
|
|
|
| Obs2 |
= |
|
0.5203 |
* |
f1 |
+ |
1.0000 |
|
e2 |
| |
|
|
|
|
x2 |
|
|
|
|
| Obs3 |
= |
|
0.4874 |
* |
f1 |
+ |
1.0000 |
|
e3 |
| |
|
|
|
|
x3 |
|
|
|
|
| Obs4 |
= |
|
0.5211 |
* |
f2 |
+ |
1.0000 |
|
e4 |
| |
|
|
|
|
x4 |
|
|
|
|
| Obs5 |
= |
|
0.4971 |
* |
f2 |
+ |
1.0000 |
|
e5 |
| |
|
|
|
|
x5 |
|
|
|
|
| Obs6 |
= |
|
0.4381 |
* |
f2 |
+ |
1.0000 |
|
e6 |
| |
|
|
|
|
x6 |
|
|
|
|
| Obs7 |
= |
|
0.4524 |
* |
f3 |
+ |
1.0000 |
|
e7 |
| |
|
|
|
|
x7 |
|
|
|
|
| Obs8 |
= |
|
0.4173 |
* |
f3 |
+ |
1.0000 |
|
e8 |
| |
|
|
|
|
x8 |
|
|
|
|
| Obs9 |
= |
|
0.4076 |
* |
f3 |
+ |
1.0000 |
|
e9 |
| |
|
|
|
|
x9 |
|
|
|
|
| f1 |
= |
|
1.4438 |
* |
f4 |
+ |
1.0000 |
|
e10 |
| |
|
|
|
|
x10 |
|
|
|
|
| f2 |
= |
|
1.2538 |
* |
f4 |
+ |
1.0000 |
|
e11 |
| |
|
|
|
|
x11 |
|
|
|
|
| f3 |
= |
|
1.4065 |
* |
f4 |
+ |
1.0000 |
|
e12 |
| |
|
|
|
|
x12 |
|
|
|
|
| |
1.00000 |
| u1 |
0.18150 |
| u2 |
0.16493 |
| u3 |
0.26713 |
| u4 |
0.30150 |
| u5 |
0.36450 |
| u6 |
0.50642 |
| u7 |
0.39033 |
| u8 |
0.48138 |
| u9 |
0.50509 |
| |
1.00000 |
| |
1.00000 |
| |
1.00000 |
Alternatively, you can use the COSAN model specification for analyzing the same data set. First, under the second-order factor model, the covariance structures of the observed variables can be derived as
where 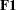 is the 9
is the 9  3 first-order loading matrix for the observed variables,
3 first-order loading matrix for the observed variables,  is the 3
is the 3  1 second-order loading matrix for the first-order factors,
1 second-order loading matrix for the first-order factors, 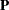 is the 1
is the 1  1 covariance matrix for the second-order factor f4,
1 covariance matrix for the second-order factor f4, 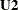 is the 3
is the 3  3 error covariance matrix of the first-order factors f1–f3 (or the covariance matrix of the error terms e10–12), and
3 error covariance matrix of the first-order factors f1–f3 (or the covariance matrix of the error terms e10–12), and  is the 9
is the 9  9 error covariance matrix for the observed variables (or the covariance matrix of the error terms e1–9).
9 error covariance matrix for the observed variables (or the covariance matrix of the error terms e1–9).
Matrix 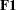 contains the loading parameters x1–x9 and matrix
contains the loading parameters x1–x9 and matrix  contains the loading parameters x10–x12. Because there is only one second-order factor f4 in the model, matrix
contains the loading parameters x10–x12. Because there is only one second-order factor f4 in the model, matrix 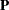 is a scalar, which is a fixed constant 1 in the LINEQS model. Matrix
is a scalar, which is a fixed constant 1 in the LINEQS model. Matrix 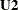 is an identity matrix because all error variances are fixed at 1 and they are not correlated. Matrix
is an identity matrix because all error variances are fixed at 1 and they are not correlated. Matrix 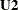 is a diagonal matrix that contains the parameters u1–u9. Given this information, you can use the following statements to specify the second-order factor model as a COSAN model:
is a diagonal matrix that contains the parameters u1–u9. Given this information, you can use the following statements to specify the second-order factor model as a COSAN model:
proc calis data=Thurst nobs=213 corr nose;
cosan
var = obs1-obs9,
F1(3) * F2(1) * P(1,IDE) + F1(3) * U2(3,IDE) + U1(9,DIA);
matrix F1
[1 , @1] = x1-x3,
[4 , @2] = x4-X6,
[7 , @3] = x7-x9;
matrix F2
[ ,1] = x10-x12;
matrix U1
[1,1] = u1-u9;
bounds
0. <= u1-u9;
vnames
F1 = [f1 f2 f3],
F2 = [f4],
U1 = [e1-e9];
run;
In the PROC CALIS statement, you specify the observed variables in the VAR= option and the covariance structures for the observed variables. In the terms of the covariance structure formula, you need to specify the expressions only up the central symmetric matrices. The latter parts of these expressions are redundant and can be generated automatically by PROC CALIS, as shown in Output 26.29.2.
Output 26.29.2
The Covariance Structures and Model Matrices of the Second-Order Factor Model: COSAN Model
| Sigma = |
F1*F2*P*F2`*F1` + F1*U2*F1` + U1 |
| F1 |
9 |
3 |
GEN: Rectangular |
| F2 |
3 |
1 |
GEN: Vector |
| P |
1 |
1 |
IDE: Identity |
| U1 |
9 |
9 |
DIA: Diagonal |
| U2 |
3 |
3 |
IDE: Identity |
Output 26.29.2 shows that the intended covariance structures for the observed variables are being analyzed. The matrix types are shown next. Matrix  is a rectangular matrix and matrix
is a rectangular matrix and matrix  is a vector, although they have the default general (GEN) matrix type. Matrices
is a vector, although they have the default general (GEN) matrix type. Matrices 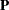 and
and 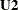 are fixed identity (IDE) matrices in the model. For these two matrices, you do not need to specify any of their elements by using the MATRIX statement because they are already well-defined with the IDE type. Lastly, matrix
are fixed identity (IDE) matrices in the model. For these two matrices, you do not need to specify any of their elements by using the MATRIX statement because they are already well-defined with the IDE type. Lastly, matrix  is a diagonal (DIA) matrix in the model.
is a diagonal (DIA) matrix in the model.
Output 26.29.3 shows the estimates of the first-order factor loading matrix 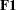 .
.
Output 26.29.3
Estimation of the 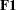 Matrix of the Second-Order Factor Model: COSAN Model
Matrix of the Second-Order Factor Model: COSAN Model
In the MATRIX statement for 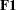 , you specify the pattern of the loadings. In the first entry of the MATRIX statement, you specify the loadings in the following elements: [1,1], [2,1], and [3,1]. They are free parameters x1–x3, respectively. Notice that the @ sign is necessary in the first entry because the elements being defined would have been [1,1], [2,2], and [3,3] otherwise. The @ sign fixes the column number to 1. See the MATRIX statement for more details about the notation. Similarly, you define the other clusters of loading in the second and third entries in the MATRIX statement for
, you specify the pattern of the loadings. In the first entry of the MATRIX statement, you specify the loadings in the following elements: [1,1], [2,1], and [3,1]. They are free parameters x1–x3, respectively. Notice that the @ sign is necessary in the first entry because the elements being defined would have been [1,1], [2,2], and [3,3] otherwise. The @ sign fixes the column number to 1. See the MATRIX statement for more details about the notation. Similarly, you define the other clusters of loading in the second and third entries in the MATRIX statement for 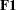 . This explains the pattern of factor loadings in Output 26.29.3. These loading estimates x1–x9 match those by the LINEQS model specification, as shown in Output 26.29.1.
. This explains the pattern of factor loadings in Output 26.29.3. These loading estimates x1–x9 match those by the LINEQS model specification, as shown in Output 26.29.1.
Output 26.29.3 shows the estimates of the second-order factor loading matrix  .
.
Output 26.29.4
Estimation of the  Matrix of the Second-Order Factor Model: COSAN Model
Matrix of the Second-Order Factor Model: COSAN Model
In the MATRIX statement for  , you do not specify the row numbers in the [ ,1] specification. PROC CALIS interprets this as stating that all the valid elements in the first column are being specified in the parameter list. In the current example, this means that elements
, you do not specify the row numbers in the [ ,1] specification. PROC CALIS interprets this as stating that all the valid elements in the first column are being specified in the parameter list. In the current example, this means that elements 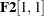 ,
,  , and
, and 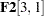 are filled with the free parameters x10, x11, and x12, respectively. Output 26.29.3 shows these specification and the corresponding estimates, which match those of the LINEQS model specification, as shown in Output 26.29.1.
are filled with the free parameters x10, x11, and x12, respectively. Output 26.29.3 shows these specification and the corresponding estimates, which match those of the LINEQS model specification, as shown in Output 26.29.1.
Output 26.29.5 shows the estimates of the error covariance matrix  .
.
Output 26.29.5
Estimation of the  Matrix of the Second-Order Factor Model: COSAN Model
Matrix of the Second-Order Factor Model: COSAN Model
In the MATRIX statement for  , you specify the diagonal elements of the matrix by using the starting element at [1,1]. The parameter assignment proceeds to [2,2], [3,3] and so on such that all the trailing parameters u1–u9 are filled. This means that the last element
, you specify the diagonal elements of the matrix by using the starting element at [1,1]. The parameter assignment proceeds to [2,2], [3,3] and so on such that all the trailing parameters u1–u9 are filled. This means that the last element 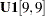 is a free parameter named u9. Output 26.29.5 confirms this intended pattern. Again, all these error variance estimates match those by the LINEQS model specification, as shown in Output 26.29.1.
is a free parameter named u9. Output 26.29.5 confirms this intended pattern. Again, all these error variance estimates match those by the LINEQS model specification, as shown in Output 26.29.1.


 Classes of Statements in PROC CALIS Single-Group Analysis Syntax Multiple-Group Multiple-Model Analysis Syntax PROC CALIS Statement BOUNDS Statement BY Statement COSAN Statement COV Statement DETERM Statement EFFPART Statement FACTOR Statement FITINDEX Statement FREQ Statement GROUP Statement LINCON Statement LINEQS Statement LISMOD Statement LMTESTS Statement MATRIX Statement MEAN Statement MODEL Statement MSTRUCT Statement NLINCON Statement NLOPTIONS Statement OUTFILES Statement PARAMETERS Statement PARTIAL Statement PATH Statement PCOV Statement PVAR Statement RAM Statement REFMODEL Statement RENAMEPARM Statement SAS Programming Statements SIMTESTS Statement STD Statement STRUCTEQ Statement TESTFUNC Statement VAR Statement VARIANCE Statement VARNAMES Statement WEIGHT Statement
Classes of Statements in PROC CALIS Single-Group Analysis Syntax Multiple-Group Multiple-Model Analysis Syntax PROC CALIS Statement BOUNDS Statement BY Statement COSAN Statement COV Statement DETERM Statement EFFPART Statement FACTOR Statement FITINDEX Statement FREQ Statement GROUP Statement LINCON Statement LINEQS Statement LISMOD Statement LMTESTS Statement MATRIX Statement MEAN Statement MODEL Statement MSTRUCT Statement NLINCON Statement NLOPTIONS Statement OUTFILES Statement PARAMETERS Statement PARTIAL Statement PATH Statement PCOV Statement PVAR Statement RAM Statement REFMODEL Statement RENAMEPARM Statement SAS Programming Statements SIMTESTS Statement STD Statement STRUCTEQ Statement TESTFUNC Statement VAR Statement VARIANCE Statement VARNAMES Statement WEIGHT Statement Input Data Sets Output Data Sets The COSAN Model The FACTOR Model The LINEQS Model The LISMOD Model and Submodels The MSTRUCT Model The PATH Model The RAM Model Naming Variables and Parameters Setting Constraints on Parameters Automatic Variable Selection Estimation Criteria Relationships among Estimation Criteria Gradient, Hessian, Information Matrix, and Approximate Standard Errors Counting the Degrees of Freedom Assessment of Fit Total, Direct, and Indirect Effects Standardized Solutions Modification Indices Missing Values and the Analysis of Missing Patterns Measures of Multivariate Kurtosis Initial Estimates Use of Optimization Techniques Computational Problems Displayed Output ODS Table Names ODS Graphics
Input Data Sets Output Data Sets The COSAN Model The FACTOR Model The LINEQS Model The LISMOD Model and Submodels The MSTRUCT Model The PATH Model The RAM Model Naming Variables and Parameters Setting Constraints on Parameters Automatic Variable Selection Estimation Criteria Relationships among Estimation Criteria Gradient, Hessian, Information Matrix, and Approximate Standard Errors Counting the Degrees of Freedom Assessment of Fit Total, Direct, and Indirect Effects Standardized Solutions Modification Indices Missing Values and the Analysis of Missing Patterns Measures of Multivariate Kurtosis Initial Estimates Use of Optimization Techniques Computational Problems Displayed Output ODS Table Names ODS Graphics Estimating Covariances and Correlations Estimating Covariances and Means Simultaneously Testing Uncorrelatedness of Variables Testing Covariance Patterns Testing Some Standard Covariance Pattern Hypotheses Linear Regression Model Multivariate Regression Models Measurement Error Models Testing Specific Measurement Error Models Measurement Error Models with Multiple Predictors Measurement Error Models Specified As Linear Equations Confirmatory Factor Models Confirmatory Factor Models: Some Variations The Full Information Maximum Likelihood Method Comparing the ML and FIML Estimation Path Analysis: Stability of Alienation Simultaneous Equations with Mean Structures and Reciprocal Paths Fitting Direct Covariance Structures Confirmatory Factor Analysis: Cognitive Abilities Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis Testing Equality of Covariance and Mean Matrices between Independent Groups Illustrating Various General Modeling Languages Testing Competing Path Models for the Career Aspiration Data Fitting a Latent Growth Curve Model Higher-Order and Hierarchical Factor Models Linear Relations among Factor Loadings Multiple-Group Model for Purchasing Behavior Fitting the RAM and EQS Models by the COSAN Modeling Language Second-Order Confirmatory Factor Analysis Linear Relations among Factor Loadings: COSAN Model Specification Ordinal Relations among Factor Loadings Longitudinal Factor Analysis
Estimating Covariances and Correlations Estimating Covariances and Means Simultaneously Testing Uncorrelatedness of Variables Testing Covariance Patterns Testing Some Standard Covariance Pattern Hypotheses Linear Regression Model Multivariate Regression Models Measurement Error Models Testing Specific Measurement Error Models Measurement Error Models with Multiple Predictors Measurement Error Models Specified As Linear Equations Confirmatory Factor Models Confirmatory Factor Models: Some Variations The Full Information Maximum Likelihood Method Comparing the ML and FIML Estimation Path Analysis: Stability of Alienation Simultaneous Equations with Mean Structures and Reciprocal Paths Fitting Direct Covariance Structures Confirmatory Factor Analysis: Cognitive Abilities Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis Testing Equality of Covariance and Mean Matrices between Independent Groups Illustrating Various General Modeling Languages Testing Competing Path Models for the Career Aspiration Data Fitting a Latent Growth Curve Model Higher-Order and Hierarchical Factor Models Linear Relations among Factor Loadings Multiple-Group Model for Purchasing Behavior Fitting the RAM and EQS Models by the COSAN Modeling Language Second-Order Confirmatory Factor Analysis Linear Relations among Factor Loadings: COSAN Model Specification Ordinal Relations among Factor Loadings Longitudinal Factor Analysis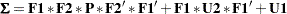
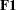 is the 9
is the 9  3 first-order loading matrix for the observed variables,
3 first-order loading matrix for the observed variables,  is the 3
is the 3  1 second-order loading matrix for the first-order factors,
1 second-order loading matrix for the first-order factors, 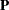 is the 1
is the 1  1 covariance matrix for the second-order factor f4,
1 covariance matrix for the second-order factor f4, 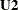 is the 3
is the 3  3 error covariance matrix of the first-order factors f1–f3 (or the covariance matrix of the error terms e10–12), and
3 error covariance matrix of the first-order factors f1–f3 (or the covariance matrix of the error terms e10–12), and  is the 9
is the 9  9 error covariance matrix for the observed variables (or the covariance matrix of the error terms e1–9).
9 error covariance matrix for the observed variables (or the covariance matrix of the error terms e1–9). 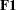 contains the loading parameters x1–x9 and matrix
contains the loading parameters x1–x9 and matrix  contains the loading parameters x10–x12. Because there is only one second-order factor f4 in the model, matrix
contains the loading parameters x10–x12. Because there is only one second-order factor f4 in the model, matrix 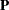 is a scalar, which is a fixed constant 1 in the LINEQS model. Matrix
is a scalar, which is a fixed constant 1 in the LINEQS model. Matrix 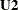 is an identity matrix because all error variances are fixed at 1 and they are not correlated. Matrix
is an identity matrix because all error variances are fixed at 1 and they are not correlated. Matrix 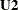 is a diagonal matrix that contains the parameters u1–u9. Given this information, you can use the following statements to specify the second-order factor model as a COSAN model:
is a diagonal matrix that contains the parameters u1–u9. Given this information, you can use the following statements to specify the second-order factor model as a COSAN model: 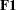 is a rectangular matrix and matrix
is a rectangular matrix and matrix  is a vector, although they have the default general (GEN) matrix type. Matrices
is a vector, although they have the default general (GEN) matrix type. Matrices 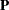 and
and 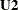 are fixed identity (IDE) matrices in the model. For these two matrices, you do not need to specify any of their elements by using the MATRIX statement because they are already well-defined with the IDE type. Lastly, matrix
are fixed identity (IDE) matrices in the model. For these two matrices, you do not need to specify any of their elements by using the MATRIX statement because they are already well-defined with the IDE type. Lastly, matrix  is a diagonal (DIA) matrix in the model.
is a diagonal (DIA) matrix in the model. 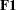 .
. 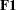 Matrix of the Second-Order Factor Model: COSAN Model
Matrix of the Second-Order Factor Model: COSAN Model
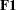 , you specify the pattern of the loadings. In the first entry of the MATRIX statement, you specify the loadings in the following elements: [1,1], [2,1], and [3,1]. They are free parameters x1–x3, respectively. Notice that the @ sign is necessary in the first entry because the elements being defined would have been [1,1], [2,2], and [3,3] otherwise. The @ sign fixes the column number to 1. See the MATRIX statement for more details about the notation. Similarly, you define the other clusters of loading in the second and third entries in the MATRIX statement for
, you specify the pattern of the loadings. In the first entry of the MATRIX statement, you specify the loadings in the following elements: [1,1], [2,1], and [3,1]. They are free parameters x1–x3, respectively. Notice that the @ sign is necessary in the first entry because the elements being defined would have been [1,1], [2,2], and [3,3] otherwise. The @ sign fixes the column number to 1. See the MATRIX statement for more details about the notation. Similarly, you define the other clusters of loading in the second and third entries in the MATRIX statement for 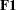 . This explains the pattern of factor loadings in Output 26.29.3. These loading estimates x1–x9 match those by the LINEQS model specification, as shown in Output 26.29.1.
. This explains the pattern of factor loadings in Output 26.29.3. These loading estimates x1–x9 match those by the LINEQS model specification, as shown in Output 26.29.1.  .
.  Matrix of the Second-Order Factor Model: COSAN Model
Matrix of the Second-Order Factor Model: COSAN Model
 , you do not specify the row numbers in the [ ,1] specification. PROC CALIS interprets this as stating that all the valid elements in the first column are being specified in the parameter list. In the current example, this means that elements
, you do not specify the row numbers in the [ ,1] specification. PROC CALIS interprets this as stating that all the valid elements in the first column are being specified in the parameter list. In the current example, this means that elements 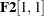 ,
,  , and
, and 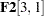 are filled with the free parameters x10, x11, and x12, respectively. Output 26.29.3 shows these specification and the corresponding estimates, which match those of the LINEQS model specification, as shown in Output 26.29.1.
are filled with the free parameters x10, x11, and x12, respectively. Output 26.29.3 shows these specification and the corresponding estimates, which match those of the LINEQS model specification, as shown in Output 26.29.1.  .
.  Matrix of the Second-Order Factor Model: COSAN Model
Matrix of the Second-Order Factor Model: COSAN Model
 , you specify the diagonal elements of the matrix by using the starting element at [1,1]. The parameter assignment proceeds to [2,2], [3,3] and so on such that all the trailing parameters u1–u9 are filled. This means that the last element
, you specify the diagonal elements of the matrix by using the starting element at [1,1]. The parameter assignment proceeds to [2,2], [3,3] and so on such that all the trailing parameters u1–u9 are filled. This means that the last element 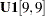 is a free parameter named u9. Output 26.29.5 confirms this intended pattern. Again, all these error variance estimates match those by the LINEQS model specification, as shown in Output 26.29.1.
is a free parameter named u9. Output 26.29.5 confirms this intended pattern. Again, all these error variance estimates match those by the LINEQS model specification, as shown in Output 26.29.1.