The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALIS Single-Group Analysis Syntax Multiple-Group Multiple-Model Analysis Syntax PROC CALIS Statement BOUNDS Statement BY Statement COSAN Statement COV Statement DETERM Statement EFFPART Statement FACTOR Statement FITINDEX Statement FREQ Statement GROUP Statement LINCON Statement LINEQS Statement LISMOD Statement LMTESTS Statement MATRIX Statement MEAN Statement MODEL Statement MSTRUCT Statement NLINCON Statement NLOPTIONS Statement OUTFILES Statement PARAMETERS Statement PARTIAL Statement PATH Statement PCOV Statement PVAR Statement RAM Statement REFMODEL Statement RENAMEPARM Statement SAS Programming Statements SIMTESTS Statement STD Statement STRUCTEQ Statement TESTFUNC Statement VAR Statement VARIANCE Statement VARNAMES Statement WEIGHT Statement
Classes of Statements in PROC CALIS Single-Group Analysis Syntax Multiple-Group Multiple-Model Analysis Syntax PROC CALIS Statement BOUNDS Statement BY Statement COSAN Statement COV Statement DETERM Statement EFFPART Statement FACTOR Statement FITINDEX Statement FREQ Statement GROUP Statement LINCON Statement LINEQS Statement LISMOD Statement LMTESTS Statement MATRIX Statement MEAN Statement MODEL Statement MSTRUCT Statement NLINCON Statement NLOPTIONS Statement OUTFILES Statement PARAMETERS Statement PARTIAL Statement PATH Statement PCOV Statement PVAR Statement RAM Statement REFMODEL Statement RENAMEPARM Statement SAS Programming Statements SIMTESTS Statement STD Statement STRUCTEQ Statement TESTFUNC Statement VAR Statement VARIANCE Statement VARNAMES Statement WEIGHT Statement -
Details
 Input Data Sets Output Data Sets The COSAN Model The FACTOR Model The LINEQS Model The LISMOD Model and Submodels The MSTRUCT Model The PATH Model The RAM Model Naming Variables and Parameters Setting Constraints on Parameters Automatic Variable Selection Estimation Criteria Relationships among Estimation Criteria Gradient, Hessian, Information Matrix, and Approximate Standard Errors Counting the Degrees of Freedom Assessment of Fit Total, Direct, and Indirect Effects Standardized Solutions Modification Indices Missing Values and the Analysis of Missing Patterns Measures of Multivariate Kurtosis Initial Estimates Use of Optimization Techniques Computational Problems Displayed Output ODS Table Names ODS Graphics
Input Data Sets Output Data Sets The COSAN Model The FACTOR Model The LINEQS Model The LISMOD Model and Submodels The MSTRUCT Model The PATH Model The RAM Model Naming Variables and Parameters Setting Constraints on Parameters Automatic Variable Selection Estimation Criteria Relationships among Estimation Criteria Gradient, Hessian, Information Matrix, and Approximate Standard Errors Counting the Degrees of Freedom Assessment of Fit Total, Direct, and Indirect Effects Standardized Solutions Modification Indices Missing Values and the Analysis of Missing Patterns Measures of Multivariate Kurtosis Initial Estimates Use of Optimization Techniques Computational Problems Displayed Output ODS Table Names ODS Graphics -
Examples
 Estimating Covariances and Correlations Estimating Covariances and Means Simultaneously Testing Uncorrelatedness of Variables Testing Covariance Patterns Testing Some Standard Covariance Pattern Hypotheses Linear Regression Model Multivariate Regression Models Measurement Error Models Testing Specific Measurement Error Models Measurement Error Models with Multiple Predictors Measurement Error Models Specified As Linear Equations Confirmatory Factor Models Confirmatory Factor Models: Some Variations The Full Information Maximum Likelihood Method Comparing the ML and FIML Estimation Path Analysis: Stability of Alienation Simultaneous Equations with Mean Structures and Reciprocal Paths Fitting Direct Covariance Structures Confirmatory Factor Analysis: Cognitive Abilities Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis Testing Equality of Covariance and Mean Matrices between Independent Groups Illustrating Various General Modeling Languages Testing Competing Path Models for the Career Aspiration Data Fitting a Latent Growth Curve Model Higher-Order and Hierarchical Factor Models Linear Relations among Factor Loadings Multiple-Group Model for Purchasing Behavior Fitting the RAM and EQS Models by the COSAN Modeling Language Second-Order Confirmatory Factor Analysis Linear Relations among Factor Loadings: COSAN Model Specification Ordinal Relations among Factor Loadings Longitudinal Factor Analysis
Estimating Covariances and Correlations Estimating Covariances and Means Simultaneously Testing Uncorrelatedness of Variables Testing Covariance Patterns Testing Some Standard Covariance Pattern Hypotheses Linear Regression Model Multivariate Regression Models Measurement Error Models Testing Specific Measurement Error Models Measurement Error Models with Multiple Predictors Measurement Error Models Specified As Linear Equations Confirmatory Factor Models Confirmatory Factor Models: Some Variations The Full Information Maximum Likelihood Method Comparing the ML and FIML Estimation Path Analysis: Stability of Alienation Simultaneous Equations with Mean Structures and Reciprocal Paths Fitting Direct Covariance Structures Confirmatory Factor Analysis: Cognitive Abilities Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis Testing Equality of Covariance and Mean Matrices between Independent Groups Illustrating Various General Modeling Languages Testing Competing Path Models for the Career Aspiration Data Fitting a Latent Growth Curve Model Higher-Order and Hierarchical Factor Models Linear Relations among Factor Loadings Multiple-Group Model for Purchasing Behavior Fitting the RAM and EQS Models by the COSAN Modeling Language Second-Order Confirmatory Factor Analysis Linear Relations among Factor Loadings: COSAN Model Specification Ordinal Relations among Factor Loadings Longitudinal Factor Analysis - References
| PROC CALIS Statement |
This statement invokes the procedure. There are many options in the PROC CALIS statement. These options, together with brief descriptions, are classified into different categories in the next few sections. An alphabetical listing of these options with more details then follows.
Data Set Options
You can use the following options to specify input and output data sets:
Option |
Description |
|---|---|
Inputs the data |
|
Inputs the initial values and constraints |
|
Inputs the model specifications |
|
Inputs the weight matrix |
|
Outputs the estimates and their covariance matrix |
|
Outputs the fit indices |
|
Outputs the model specifications |
|
Outputs the statistical results |
|
Outputs the weight matrix |
|
Inputs the generated default parameters in the INMODEL= data set |
Model and Estimation Options
You can use these options to specify details about estimation, models, and computations:
Option |
Description |
|---|---|
Analyzes correlation matrix |
|
Analyzes covariance matrix |
|
Specifies one of the built-in covariance structures |
|
Emphasizes the diagonal entries |
|
Defines number of observations by the number of error degrees of freedom |
|
Specifies that the INWGT= data set contains the inverse of the weight matrix |
|
Specifies one of the built-in mean patterns |
|
Analyzes the mean structures |
|
Specifies the estimation method |
|
Defines the number of observations |
|
Deactivates the inherited MEANSTR option |
|
Specifies the seed for randomly generated initial values |
|
Defines nobs by the number of regression df |
|
Specifies the ridge factor for the covariance matrix |
|
Specifies a constant for initial values |
|
Specifies the variance divisor |
|
Specifies the penalty weight to fit correlations |
|
Specifies the ridge factor for the weight matrix |
Options for Fit Statistics
You can use these options to modify the default behavior of fit index computations and display and to specify output file for fit indices:
Option |
Description |
|---|---|
Specifies the |
|
Specifies the |
|
Specifies the chi-square correction factor |
|
Defines the close fit value |
|
Reduces the degrees of freedom for model fit chi-square test |
|
Requests no degrees-of-freedom adjustment be made for active constraints |
|
Suppresses the printing of fit index types |
|
Specifies the output data set for storing fit indices |
These options can also be specified in the FITINDEX statement. However, to control the display of individual fit indices, you must use the ON= and OFF= options of the FITINDEX statement.
Options for Statistical Analysis
You can use these options to request specific statistical analysis and display and to set the parameters for statistical analysis:
Option |
Description |
|---|---|
Specifies the formula for computing asymptotic covariances |
|
Computes the skewness and kurtosis without bias corrections |
|
Displays total, direct, and indirect effects |
|
Displays the extended path estimates |
|
Specifies the algorithm for computing standard errors |
|
Computes and displays kurtosis |
|
Specifies the maximum number of missing patterns to display |
|
Computes modification indices |
|
Suppresses the display of missing pattern analysis |
|
Suppresses modification indices |
|
Suppresses the standardized output |
|
Suppresses standard error computations |
|
Displays analyzed and estimated moment matrix |
|
Displays the covariance matrix of estimates |
|
Computes the determination coefficients |
|
Prints parameter estimates |
|
Prints initial pattern and values |
|
Computes the latent variable covariances and score coefficients |
|
Specifies ODS Graphics selection |
|
Displays the weight matrix |
|
Specifies the type of residuals being computed |
|
Prints univariate statistics |
|
Specifies the probability limit for Wald tests |
|
Computes the standard errors |
|
Specifies the data proportion threshold for displaying the missing patterns |
Global Display Options
There are two different kinds of global display options: one is for selecting output; the other is for controlling the format or order of output.
You can use the following options to select printed output:
Option |
Description |
|---|---|
Suppresses the displayed output |
|
Displays all displayed output (ALL) |
|
Adds default displayed output |
|
Reduces default output (SHORT) |
|
Displays fit summary only (SUMMARY) |
In contrast to individual output printing options described in the section Options for Statistical Analysis, the global display options typically control more than one output or analysis. The relations between these two types of options are summarized in the following table:
Options |
PALL |
default |
PSHORT |
PSUMMARY |
|
|---|---|---|---|---|---|
fit indices |
* |
* |
* |
* |
* |
linear dependencies |
* |
* |
* |
* |
* |
* |
* |
* |
* |
||
iteration history |
* |
* |
* |
* |
|
* |
* |
* |
|||
* |
* |
* |
|||
* |
* |
* |
|||
* |
* |
||||
* |
* |
||||
* |
* |
||||
* |
* |
||||
* |
|||||
* |
|||||
* |
|||||
Each column in the table represents a global display option. An "*" in the column means that the individual output or analysis option listed in the corresponding row turns on when the global display option in the corresponding column is specified.
Note that the column labeled with "default" is for default printing. If the NOPRINT option is not specified, a default set of output is displayed. The PRINT and PALL options add to the default output, while the PSHORT and PSUMMARY options reduce from the default output.
Note also that the PCOVES, PDETERM, and PRIMAT options cannot be turned on by any global display options. They must be specified individually.
The following global display options are for controlling formats and order of the output:
Option |
Description |
|---|---|
Displays model specifications and results according to the input order |
|
Suppresses the printing of parameter names in results |
|
Orders all output displays according to the model numbers, group numbers, and parameter types |
|
Orders the group output displays according to the group numbers |
|
Orders the model output displays according to the model numbers |
|
Orders the model output displays according to the parameter types within each model |
|
Displays parameter names in model specifications and results |
|
Displays estimation results in matrix form |
Optimization Options
You can use the following options to control the behavior of the optimization. Most of these options are also available in the NLOPTIONS statement.
Option |
Description |
|---|---|
Specifies the absolute singularity criterion for inverting the information matrix |
|
Specifies the singularity tolerance of the information matrix |
|
Specifies the relative function convergence criterion |
|
Specifies the gradient convergence criterion |
|
Specifies the initial step length (RADIUS=, SALPHA=) |
|
Specifies the line-search method |
|
Specifies the line-search precision (SPRECISION=) |
|
Specifies the maximum number of function calls |
|
Specifies the maximum number of iterations |
|
Specifies the relative M singularity of the information matrix |
|
Specifies the minimization method |
|
Specifies the singularity criterion for matrix inversion |
|
Specifies the update method for some optimization techniques |
|
Specifies the relative V singularity of information matrix |
Listing of PROC CALIS Statement Options
-
ALPHAECV=

specifies a
 confidence interval (
confidence interval (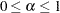 ) for the Browne and Cudeck (1993) expected cross-validation index (ECVI). The default value is
) for the Browne and Cudeck (1993) expected cross-validation index (ECVI). The default value is  , which corresponds to a 90% confidence interval for the ECVI.
, which corresponds to a 90% confidence interval for the ECVI. -
ALPHARMS=

specifies a
 confidence interval (
confidence interval (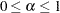 ) for the Steiger and Lind (1980) root mean square error of approximation (RMSEA) coefficient (see Browne and Du Toit 1992). The default value is
) for the Steiger and Lind (1980) root mean square error of approximation (RMSEA) coefficient (see Browne and Du Toit 1992). The default value is  , which corresponds to a 90% confidence interval for the RMSEA.
, which corresponds to a 90% confidence interval for the RMSEA. - ASINGULAR | ASING=r
-
specifies an absolute singularity criterion r (r
 ), for the inversion of the information matrix, which is needed to compute the covariance matrix. The default value for r or ASING= is the square root of the smallest positive double precision value.
), for the inversion of the information matrix, which is needed to compute the covariance matrix. The default value for r or ASING= is the square root of the smallest positive double precision value. When inverting the information matrix, the following singularity criterion is used for the diagonal pivot
 of the matrix:
of the matrix: 
where VSING and MSING are the specified values in the VSINGULAR= and MSINGULAR= options, respectively, and
 is the
is the 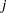 -th diagonal element of the information matrix. Note that in many cases a normalized matrix
-th diagonal element of the information matrix. Note that in many cases a normalized matrix 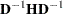 is decomposed (where
is decomposed (where  ), and the singularity criteria are modified correspondingly.
), and the singularity criteria are modified correspondingly. - ASYCOV | ASC=name
-
specifies the formula for asymptotic covariances used in the weight matrix
 for WLS and DWLS estimation. The ASYCOV option is effective only if METHOD= WLS or METHOD=DWLS and no INWGT= input data set is specified. The following formulas are implemented:
for WLS and DWLS estimation. The ASYCOV option is effective only if METHOD= WLS or METHOD=DWLS and no INWGT= input data set is specified. The following formulas are implemented: - BIASED:
Browne (1984) formula (3.4)
biased asymptotic covariance estimates; the resulting weight matrix is at least positive semidefinite. This is the default for analyzing a covariance matrix.- UNBIASED:
Browne (1984) formula (3.8)
asymptotic covariance estimates corrected for bias; the resulting weight matrix can be indefinite (that is, can have negative eigenvalues), especially for small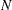 .
. - CORR:
Browne and Shapiro (1986) formula (3.2)
(identical to DeLeeuw (1983) formulas (2,3,4)) the asymptotic variances of the diagonal elements are set to the reciprocal of the value r specified by the WPENALTY= option (default: r ). This formula is the default for analyzing a correlation matrix.
). This formula is the default for analyzing a correlation matrix.
By default, AYSCOV=BIASED is used for covariance analyses and ASYCOV=CORR is used for correlation analyses. Therefore, in almost all cases you do not need to set the ASYCOV= option once you specify the covariance or correlation analysis by the COV or CORR option.
- BIASKUR
-
computes univariate skewness and kurtosis by formulas uncorrected for bias.
See the section Measures of Multivariate Kurtosis for more information.
- CHICORRECT | CHICORR= name | c
-
specifies a correction factor c for the chi-square statistics for model fit. You can specify a name for a built-in correction factor or a value between
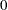 and
and  as the CHICORRECT= value. The model fit chi-square statistic is computed as:
as the CHICORRECT= value. The model fit chi-square statistic is computed as: 
where
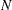 is the total number of observations,
is the total number of observations,  is the number of independent groups, and
is the number of independent groups, and 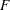 is the optimized function value. Application of these correction factors requires appropriate specification of the covariance structural model suitable for the chi-square correction. For example, using CHICORRECT=UNCORR assumes that you are fitting a covariance structure with free parameters on the diagonal elements and fixed zeros off-diagonal elements of the covariance matrix. Because all the built-in correction factors assume multivariate normality in their derivations, the appropriateness of applying these built-in chi-square corrections to estimation methods other than METHOD=ML is not known.
is the optimized function value. Application of these correction factors requires appropriate specification of the covariance structural model suitable for the chi-square correction. For example, using CHICORRECT=UNCORR assumes that you are fitting a covariance structure with free parameters on the diagonal elements and fixed zeros off-diagonal elements of the covariance matrix. Because all the built-in correction factors assume multivariate normality in their derivations, the appropriateness of applying these built-in chi-square corrections to estimation methods other than METHOD=ML is not known. Valid names for the CHICORRECT= value are as follows:
- COMPSYM | EQVARCOV
-
specifies the correction factor due to Box (1949) for testing equal variances and equal covariances in a covariance matrix. The correction factor is:

where
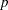 (
( )represents the number of variables and
)represents the number of variables and  , with
, with 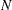 denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models.
denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models. - EQCOVMAT
-
specifies the correction factor due to Box (1949) for testing equality of covariance matrices. The correction factor is:

where
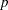 represents the number of variables,
represents the number of variables,  (
( ) represents the number of groups, and
) represents the number of groups, and  , with
, with 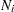 denoting the number of observations in the
denoting the number of observations in the 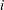 -th group. This option is not applied when you also analyze the mean structures or when you fit single-group models.
-th group. This option is not applied when you also analyze the mean structures or when you fit single-group models. - FIXCOV
-
specifies the correction factor due to Bartlett (1954) for testing a covariance matrix against a hypothetical fixed covariance matrix. The correction factor is:

where
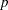 represents the number of variables and
represents the number of variables and  , with
, with 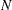 denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models.
denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models. - SPHERICITY
-
specifies the correction factor due to Box (1949) for testing a spherical covariance matrix (Mauchly; 1940). The correction factor is:

where
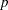 represents the number of variables and
represents the number of variables and  , with
, with 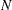 denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models.
denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models. - TYPEH
-
specifies the correction factor for testing the H pattern (Huynh and Feldt; 1970) directly. The correction factor is:

where
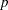 (
( ) represents the number of variables and
) represents the number of variables and  , with
, with 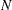 denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models.
denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models. This correction factor is derived by substituting
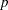 with
with  in the correction formula applied to Mauchly’s sphericity test. The reason is that testing the H pattern of
in the correction formula applied to Mauchly’s sphericity test. The reason is that testing the H pattern of 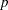 variables is equivalent to testing the sphericity of the
variables is equivalent to testing the sphericity of the  orthogonal contrasts of the same set of variables (Huynh and Feldt; 1970). See pp. 295–296 of Morrison (1990) for more details.
orthogonal contrasts of the same set of variables (Huynh and Feldt; 1970). See pp. 295–296 of Morrison (1990) for more details. - UNCORR
-
specifies the correction factor due to Bartlett (1950) and Box (1949) for testing a diagonal pattern of a covariance matrix, while the diagonal elements (variances) are unconstrained. This test is sometimes called Bartlett’s test of sphericity—not to be confused with the sphericity test dues to Mauchly (1940), which requires all variances in the covariance matrix to be equal. The correction factor is:

where
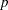 represents the number of variables and
represents the number of variables and  , with
, with 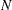 denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models.
denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean structures or when you fit multiple-group models.
- CLOSEFIT=p
defines the criterion value p for indicating a close fit. The smaller the better fit. The default value for close fit is
 .
. - CORRELATION | CORR
analyzes the correlation matrix, instead of the default covariance matrix. See the COVARIANCE option for more details.
- COVARIANCE | COV
-
analyzes the covariance matrix. Because this is also the default analysis in PROC CALIS, you can simply omit this option when you analyze covariance rather than correlation matrices. If the DATA= input data set is a TYPE=CORR data set (containing a correlation matrix and standard deviations), the default COV option means that the covariance matrix is computed and analyzed.
Unlike many other SAS/STAT procedures (for example, the FACTOR procedure) that analyze correlation matrices by default, PROC CALIS uses a different default because statistical theories of structural equation modeling or covariance structure analysis are mostly developed for covariance matrices. You must use the CORR option if correlation matrices are analyzed.
- COVPATTERN | COVPAT=name
-
specifies one of the built-in covariance structures for the data. The purpose of this option is to fit some commonly-used direct covariance structures efficiently without the explicit use of the MSTRUCT model specifications. With this option, the covariance structures are defined internally in PROC CALIS. The following names for the built-in covariance structures are supported:
- COMPSYM | EQVARCOV
-
specifies the compound symmetry pattern for the covariance matrix. That is, a covariance matrix with equal variances for all variables and equal covariance between any pairs of variables (EQVARCOV). PROC CALIS names the common variance parameter _varparm and the common covariance parameter _covparm. For example, if there are four variables in the analysis, the covariance pattern generated by PROC CALIS is:

If you request a single-group maximum likelihood (METHOD=ML) covariance structure analysis by specifying the COVPATTERN=COMPSYM or COVPATTERN=EQVARCOV option and the mean structures are not modeled, the chi-square correction due to Box (1949) is applied automatically when the number of variables is greater than or equal to 2. See the CHICORRECT=COMPSYM option for the definition of the correction factor.
- EQCOVMAT
-
specifies the equality of covariance matrices between multiple groups. That is, this option tests the null hypothesis that

where
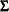 is a common covariance matrix for the
is a common covariance matrix for the 
 ’s (
’s ( ). The elements of
). The elements of 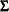 are named _cov_xx_yy automatically by PROC CALIS, where xx represents the row number and yy represents the column number. For example, if there are four variables in the analysis, the common
are named _cov_xx_yy automatically by PROC CALIS, where xx represents the row number and yy represents the column number. For example, if there are four variables in the analysis, the common 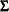 is defined as:
is defined as: 
If you request a multiple-group maximum likelihood (METHOD=ML) covariance structure analysis by specifying the COVPATTERN=EQCOVMAT and the mean structures are not modeled, the chi-square correction due to Box (1949) is applied automatically. See the CHICORRECT=EQCOVMAT option for the definition of the correction factor.
- SATURATED
-
specifies a saturated covariance structure model. This is the default option when you specify the MEANPATTERN= option without using the COVPATTERN= option. The elements of
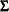 are named _cov_xx_yy automatically by PROC CALIS, where xx represents the row number and yy represents the column number. For example, if there are three variables in the analysis,
are named _cov_xx_yy automatically by PROC CALIS, where xx represents the row number and yy represents the column number. For example, if there are three variables in the analysis, 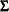 is defined as:
is defined as: 
- SPHERICITY | SIGSQI
-
specifies the spheric pattern of the covariance matrix (Mauchly; 1940). That is, this option tests the null hypothesis that

where
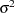 is a common variance parameter and
is a common variance parameter and  is an identity matrix. PROC CALIS names the common variance parameter _varparm. For example, if there are three variables in the analysis, the covariance pattern generated by PROC CALIS is:
is an identity matrix. PROC CALIS names the common variance parameter _varparm. For example, if there are three variables in the analysis, the covariance pattern generated by PROC CALIS is: 
If you request a single-group maximum likelihood (METHOD=ML) covariance structure analysis by specifying the COVPATTERN=SPHERICITY or COVPATTERN=SIGSQI option and the mean structures are not modeled, the chi-square correction due to Box (1949) is applied automatically. See the CHICORRECT=SPHERICITY option for the definition of the correction factor.
- UNCORR | DIAG
-
specifies the diagonal pattern of the covariance matrix. That is, this option tests the null hypothesis of uncorrelatedness—all correlations (or covariances) between variables are zero and the variances are unconstrained. PROC CALIS names the variance parameters _varparm_xx, where xx represents the row or column number. For example, if there are three variables in the analysis, the covariance pattern generated by PROC CALIS is:

If you request a single-group maximum likelihood (METHOD=ML) covariance structure analysis by specifying the COVPATTERN=UNCORR or COVPATTERN=DIAG option and the mean structures are not modeled, the chi-square correction due to Bartlett (1950) is applied automatically. See the CHICORRECT=UNCORR option for the definition of the correction factor. Under the multivariate normal assumption, COVPATTERN=UNCORR is also a test of independence of the variables in the analysis.
When you specify the covariance structure model by means of the COVPATTERN= option, you can define the set of variables in the analysis by the VAR statement (either within the scope of the PROC CALIS statement or the GROUP statements). If the VAR statement is not used, PROC CALIS uses all numerical variables in the data sets.
Except for the EQCOVMAT pattern, all other built-in covariance patterns are primarily designed for single-group analysis. However, you can still use these covariance pattern options for multiple-group situations. For example, consider the following three-group analysis:
proc calis covpattern=compsym; group 1 / data=set1; group 2 / data=set2; group 3 / data=set3; run;
In this specification, all three groups are fitted by the compound symmetry pattern. However, there would be no constraints across these groups. PROC CALIS generates two distinct parameters for each group: _varparm_mdl1 and _covparm_mdl1 for Group 1, _varparm_mdl2 and _covparm_mdl2 for Group 2, and _varparm_mdl3 and _covparm_mdl3 for Group 3. Similarly, the _mdlxx suffix, where xx represents the model number, is applied to the parameters defined by the SATURATED, SPHERICITY (or SIGSQI), and UNCORR (or DIAG) covariance patterns in multiple-group situations. However, chi-square correction, whenever it is applicable to single-group analysis, is not applied to such multiple-group analyses.
You can also apply the COVPATTERN= option partially to the groups in the analysis. For example, the following statements apply the spheric pattern to Group 1 and Group 2 only:
proc calis covpattern=sphericity; group 1 / data=set1; group 2 / data=set2; group 3 / data=set3; model 3 / group=3; path x1 ---> y3; run;Group 3 is fitted by Model 3, which is specified explicitly by a PATH model with distinct covariance structures.
If the EQCOVMAT pattern is specified instead, as shown in the following statements, the equality of covariance matrices still holds for Groups 1 and 2:
proc calis covpattern=eqcovmat; group 1 / data=set1; group 2 / data=set2; group 3 / data=set3; model 3 / group=3; path x1 ---> y3; run;However, Group 3 has it own covariances structures as specified in Model 3. In this case, the chi-square correction due to Box (1949) is not applied because the null hypothesis is no longer testing the equality of covariance matrices among the groups in the analysis.
Use the MEANPATTERN= option if you also want to analyze some built-in mean structures along with the covariance structures.
- COVSING=r
specifies a nonnegative threshold r, which determines whether the eigenvalues of the information matrix are considered to be zero. If the inverse of the information matrix is found to be singular (depending on the VSINGULAR=, MSINGULAR=, ASINGULAR=, or SINGULAR= option), a generalized inverse is computed using the eigenvalue decomposition of the singular matrix. Those eigenvalues smaller than r are considered to be zero. If a generalized inverse is computed and you do not specify the NOPRINT option, the distribution of eigenvalues is displayed.
- DATA=SAS-data-set
specifies an input data set that can be an ordinary SAS data set or a specially structured TYPE=CORR, TYPE=COV, TYPE=UCORR, TYPE=UCOV, TYPE=SSCP, or TYPE=FACTOR SAS data set, as described in the section Input Data Sets. If the DATA= option is omitted, the most recently created SAS data set is used.
- DEMPHAS | DE=r
-
changes the initial values of all variance parameters by the relationship:

where
 is the new initial value and
is the new initial value and  is the original initial value. The initial values of all variance parameters should always be nonnegative to generate positive definite predicted model matrices in the first iteration. By using values of
is the original initial value. The initial values of all variance parameters should always be nonnegative to generate positive definite predicted model matrices in the first iteration. By using values of  , for example,
, for example,  ,
,  , and so on, you can increase these initial values to produce predicted model matrices with high positive eigenvalues in the first iteration. The DEMPHAS= option is effective independent of the way the initial values are set; that is, it changes the initial values set in the model specification as well as those set by an INMODEL= data set and those automatically generated for the FACTOR, LINEQS, LISMOD, PATH, or RAM models. It also affects the initial values set by the START= option, which uses, by default, DEMPHAS=100 if a covariance matrix is analyzed and DEMPHAS=10 for a correlation matrix.
, and so on, you can increase these initial values to produce predicted model matrices with high positive eigenvalues in the first iteration. The DEMPHAS= option is effective independent of the way the initial values are set; that is, it changes the initial values set in the model specification as well as those set by an INMODEL= data set and those automatically generated for the FACTOR, LINEQS, LISMOD, PATH, or RAM models. It also affects the initial values set by the START= option, which uses, by default, DEMPHAS=100 if a covariance matrix is analyzed and DEMPHAS=10 for a correlation matrix. - DFREDUCE | DFRED=i
reduces the degrees of freedom of the model fit
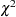 test by i. In general, the number of degrees of freedom is the total number of nonredundant elements in all moment matrices minus the number of parameters,
test by i. In general, the number of degrees of freedom is the total number of nonredundant elements in all moment matrices minus the number of parameters,  . Because negative values of i are allowed, you can also increase the number of degrees of freedom by using this option.
. Because negative values of i are allowed, you can also increase the number of degrees of freedom by using this option. - EDF | DFE=n
makes the effective number of observations
 . You can also use the NOBS= option to specify the number of observations.
. You can also use the NOBS= option to specify the number of observations. - EFFPART | PARTEFF | TOTEFF | TE
-
computes and displays total, direct, and indirect effects for the unstandardized and standardized estimation results. Standard errors for the effects are also computed. Note that this displayed output is not automatically included in the output generated by the PALL option.
Note also that in some situations computations of total effects and their partitioning are not appropriate. While total and indirect effects must converge in recursive models (models with no cyclic paths among variables), they do not always converge in nonrecursive models. When total or indirect effects do not converge, it is not appropriate to partition the effects. Therefore, before partitioning the total effects, the convergence criterion must be met. To check the convergence of the effects, PROC CALIS computes and displays the "stability coefficient of reciprocal causation"— that is, the largest modulus of the eigenvalues of the
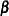 matrix, which is the square matrix that contains the path coefficients of all endogenous variables in the model. Stability coefficients less than one provide a necessary and sufficient condition for the convergence of the total and the indirect effects. Otherwise, PROC CALIS does not show results for total effects and their partitioning. See the section Stability Coefficient of Reciprocal Causation for more information about the computation of the stability coefficient.
matrix, which is the square matrix that contains the path coefficients of all endogenous variables in the model. Stability coefficients less than one provide a necessary and sufficient condition for the convergence of the total and the indirect effects. Otherwise, PROC CALIS does not show results for total effects and their partitioning. See the section Stability Coefficient of Reciprocal Causation for more information about the computation of the stability coefficient. - EXTENDPATH | GENPATH
displays the extended path estimates such as the variances, covariances, means, and intercepts in the table that contains the ordinary path effect (coefficient) estimates. This option applies to the PATH model only.
- FCONV | FTOL=r
-
specifies the relative function convergence criterion. The optimization process is terminated when the relative difference of the function values of two consecutive iterations is smaller than the specified value of r; that is,

where FSIZE can be defined by the FSIZE= option in the NLOPTIONS statement. The default value is
 , where FDIGITS either can be specified in the NLOPTIONS statement or is set by default to
, where FDIGITS either can be specified in the NLOPTIONS statement or is set by default to  , where
, where  is the machine precision.
is the machine precision. - G4=i
-
instructs that the algorithm to compute the approximate covariance matrix of parameter estimates used for computing the approximate standard errors and modification indices when the information matrix is singular. If the number of parameters
 used in the model you analyze is smaller than the value of i, the time-expensive Moore-Penrose (G4) inverse of the singular information matrix is computed by eigenvalue decomposition. Otherwise, an inexpensive pseudo (G1) inverse is computed by sweeping. By default,
used in the model you analyze is smaller than the value of i, the time-expensive Moore-Penrose (G4) inverse of the singular information matrix is computed by eigenvalue decomposition. Otherwise, an inexpensive pseudo (G1) inverse is computed by sweeping. By default,  .
. See the section Estimation Criteria for more details.
- GCONV | GTOL=r
-
specifies the relative gradient convergence criterion.
Termination of all techniques (except the CONGRA technique) requires the following normalized predicted function reduction to be smaller than r. That is,

where FSIZE can be defined by the FSIZE= option in the NLOPTIONS statement. For the CONGRA technique (where a reliable Hessian estimate
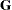 is not available),
is not available), 
is used. The default value is
 .
. - INEST | INVAR | ESTDATA=SAS-data-set
specifies an input data set that contains initial estimates for the parameters used in the optimization process and can also contain boundary and general linear constraints on the parameters. Typical applications of this option are to specify an OUTEST= data set from a previous PROC CALIS analysis. The initial estimates are taken from the values of the PARMS observation in the INEST= data set.
- INMODEL | INRAM=SAS-data-set
-
specifies an input data set that contains information about the analysis model. A typical use of the INMODEL= option is when you run an analysis with its model specifications saved as an OUTMODEL= data set from a previous PROC CALIS run. Instead of specifying the main or subsidiary model specification statements in the new run, you use the INMODEL= option to input the model specification saved from the previous run.
Sometimes, you might create an INMODEL= data set from modifying an existing OUTMODEL= data set. However, editing and modifying OUTMODEL= data sets requires good understanding of the formats and contents of the OUTMODEL= data sets. This process could be error-prone for novice users. For details about the format of INMODEL= or OUTMODEL= data sets, see the sectionInput Data Sets.
It is important to realize that INMODEL= or OUTMODEL= data sets contain only the information about the specification of the model. These data sets do not store any information about the bounds on parameters, linear and nonlinear parametric constraints, and programming statements for computing dependent parameters. If required, these types of information must be provided in the corresponding statement specifications (for example, BOUNDS, LINCON, and so on) in addition to the INMODEL = data set.
An OUTMODEL= data set might also contain default parameters added automatically by PROC CALIS from a previous run (for example, observations with _TYPE_=ADDPCOV, ADDMEAN, or ADDPVAR). When reading the OUTMODEL= model specification as an INMODEL= data set in a new run, PROC CALIS ignores these added parameters so that the model being read is exactly like the previous PROC CALIS specification (that is, before default parameters were added automatically). After interpreting the specification in the INMODEL= data set, PROC CALIS will then add default parameters appropriate to the new run. The purpose of doing this is to avoid inadvertent parameter constraints in the new run, where another set of automatic default parameters might have the same generated names as those of the generated parameter names in the INMODEL= data set.
If you want the default parameters in the INMODEL= data set to be read as a part of model specification, you must also specify the READADDPARM option. However, using the READADDPARM option should be rare.
- INSTEP=r
-
For highly nonlinear objective functions, such as the EXP function, the default initial radius of the trust-region algorithms (TRUREG, DBLDOG, and LEVMAR) or the default step length of the line-search algorithms can produce arithmetic overflows. If an arithmetic overflow occurs, specify decreasing values of
 r
r  such as INSTEP=1E
such as INSTEP=1E 1, INSTEP=1E
1, INSTEP=1E 2, INSTEP=1E
2, INSTEP=1E 4, and so on, until the iteration starts successfully.
4, and so on, until the iteration starts successfully. For trust-region algorithms (TRUREG, DBLDOG, and LEVMAR), the INSTEP option specifies a positive factor for the initial radius of the trust region. The default initial trust-region radius is the length of the scaled gradient, and it corresponds to the default radius factor of
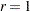 .
. For line-search algorithms (NEWRAP, CONGRA, and QUANEW), INSTEP specifies an upper bound for the initial step length for the line search during the first five iterations. The default initial step length is
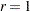 .
.
For more details, see the section Computational Problems.
- INWGT | INWEIGHT<(INV)>=SAS-data-set
specifies an input data set that contains the weight matrix
 used in generalized least squares (GLS), weighted least squares (WLS, ADF), or diagonally weighted least squares (DWLS) estimation, if you do not specify the INV option at the same time. The weight matrix must be positive definite because its inverse must be defined in the computation of the objective function. If the weight matrix
used in generalized least squares (GLS), weighted least squares (WLS, ADF), or diagonally weighted least squares (DWLS) estimation, if you do not specify the INV option at the same time. The weight matrix must be positive definite because its inverse must be defined in the computation of the objective function. If the weight matrix  defined by an INWGT= data set is not positive definite, it can be ridged using the WRIDGE= option. See the section Estimation Criteria for more information. If you specify the INWGT(INV)= option, the INWGT= data set contains the inverse of the weight matrix, rather than the weight matrix itself. Specifying the INWGT(INV)= option is equivalent to specifying the INWGT= and INWGTINV options simultaneously. With the INWGT(INV)= specification, the input matrix is not required to be positive definite. See the INWGTINV option for more details. If no INWGT= data set is specified, default settings for the weight matrices are used in the estimation process. The INWGT= data set is described in the section Input Data Sets. Typically, this input data set is an OUTWGT= data set from a previous PROC CALIS analysis.
defined by an INWGT= data set is not positive definite, it can be ridged using the WRIDGE= option. See the section Estimation Criteria for more information. If you specify the INWGT(INV)= option, the INWGT= data set contains the inverse of the weight matrix, rather than the weight matrix itself. Specifying the INWGT(INV)= option is equivalent to specifying the INWGT= and INWGTINV options simultaneously. With the INWGT(INV)= specification, the input matrix is not required to be positive definite. See the INWGTINV option for more details. If no INWGT= data set is specified, default settings for the weight matrices are used in the estimation process. The INWGT= data set is described in the section Input Data Sets. Typically, this input data set is an OUTWGT= data set from a previous PROC CALIS analysis. - INWGTINV
specifies that the INWGT= data set contains the inverse of the weight matrix, rather than the weight matrix itself. This option is effective only with an input weight matrix specified in the INWGT= data set and with the generalized least squares (GLS), weighted least squares (WLS or ADF), or diagonally weighted least squares (DWLS) estimation. With this option, the input matrix provided in the INWGT= data set is not required to be positive definite. Also, the ridging requested by the WRIDGE= option is ignored when you specify the INWGTINV option.
- KURTOSIS | KU
computes and displays univariate kurtosis and skewness, various coefficients of multivariate kurtosis, and the numbers of observations that contribute most to the normalized multivariate kurtosis. See the section Measures of Multivariate Kurtosis for more information. Using the KURTOSIS option implies the SIMPLE display option. This information is computed only if the DATA= data set is a raw data set, and it is displayed by default if the PRINT option is specified. The multivariate least squares kappa and the multivariate mean kappa are displayed only if you specify METHOD=WLS and the weight matrix is computed from an input raw data set. All measures of skewness and kurtosis are corrected for the mean. Using the BIASKUR option displays the biased values of univariate skewness and kurtosis.
- LINESEARCH | LIS | SMETHOD | SM=i
-
specifies the line-search method for the CONGRA, QUANEW, and NEWRAP optimization techniques. Refer to Fletcher (1980) for an introduction to line-search techniques. The value of i can be any integer between
 and
and  , inclusively; the default is i
, inclusively; the default is i .
. - LIS=1
specifies a line-search method that needs the same number of function and gradient calls for cubic interpolation and cubic extrapolation; this method is similar to one used by the Harwell subroutine library.
- LIS=2
specifies a line-search method that needs more function calls than gradient calls for quadratic and cubic interpolation and cubic extrapolation; this method is implemented as shown in Fletcher (1987) and can be modified to an exact line search by using the LSPRECISION= option.
- LIS=3
specifies a line-search method that needs the same number of function and gradient calls for cubic interpolation and cubic extrapolation; this method is implemented as shown in Fletcher (1987) and can be modified to an exact line search by using the LSPRECISION= option.
- LIS=4
specifies a line-search method that needs the same number of function and gradient calls for stepwise extrapolation and cubic interpolation.
- LIS=5
specifies a line-search method that is a modified version of LIS=4.
- LIS=6
specifies golden-section line search (Polak; 1971), which uses only function values for linear approximation.
- LIS=7
specifies bisection line search (Polak; 1971), which uses only function values for linear approximation.
- LIS=8
specifies the Armijo line-search technique (Polak; 1971), which uses only function values for linear approximation.
- LSPRECISION | LSP=r
- SPRECISION | SP=r
-
specifies the degree of accuracy that should be obtained by the line-search algorithms LIS=2 and LIS=3. Usually an imprecise line search is inexpensive and successful. For more difficult optimization problems, a more precise and more expensive line search might be necessary (Fletcher; 1980, p. 22). The second (default for NEWRAP, QUANEW, and CONGRA) and third line-search methods approach exact line search for small LSPRECISION= values. If you have numerical problems, you should decrease the LSPRECISION= value to obtain a more precise line search. The default LSPRECISION= values are displayed in the following table.
OMETHOD=
UPDATE=
LSP default
QUANEW
DBFGS, BFGS
r = 0.4
QUANEW
DDFP, DFP
r = 0.06
CONGRA
all
r = 0.1
NEWRAP
no update
r = 0.9
For more details, refer to Fletcher (1980, pp. 25–29).
- MAXFUNC | MAXFU=i
-
specifies the maximum number i of function calls in the optimization process. The default values are displayed in the following table.
OMETHOD=
MAXFUNC default
LEVMAR, NEWRAP, NRRIDG, TRUREG
i = 125
DBLDOG, QUANEW
i = 500
CONGRA
i = 1000
The default is used if you specify MAXFUNC=0. The optimization can be terminated only after completing a full iteration. Therefore, the number of function calls that is actually performed can exceed the number that is specified by the MAXFUNC= option.
- MAXITER | MAXIT=i <n>
-
specifies the maximum number i of iterations in the optimization process. The default values are displayed in the following table.
OMETHOD=
MAXITER default
LEVMAR, NEWRAP, NRRIDG, TRUREG
i = 50
DBLDOG, QUANEW
i = 200
CONGRA
i = 400
The default is used if you specify MAXITER=0 or if you omit the MAXITER option.
The optional second value
 is valid only for OMETHOD=QUANEW with nonlinear constraints. It specifies an upper bound
is valid only for OMETHOD=QUANEW with nonlinear constraints. It specifies an upper bound  for the number of iterations of an algorithm and reduces the violation of nonlinear constraints at a starting point. The default is
for the number of iterations of an algorithm and reduces the violation of nonlinear constraints at a starting point. The default is  =20. For example, specifying
=20. For example, specifying maxiter= . 0
means that you do not want to exceed the default number of iterations during the main optimization process and that you want to suppress the feasible point algorithm for nonlinear constraints.
- MAXMISSPAT=n
-
specifies the maximum number of missing patterns to display in the output, where n is between 1 and 9,999. The default MAXMISSPAT= value is 10 or the number of missing patterns in the data, whichever is smaller. The number of missing patterns to display cannot exceed this MAXMISSPAT= value. This option is relevant only when there are incomplete observations (with some missing values in the analysis variables) in the input raw data set and when you use METHOD=FIML or METHOD=LSFIML for estimation.
Because the number of missing patterns could be quite large, PROC CALIS displays a limited number of the most frequent missing patterns in the output. The MAXMISSPAT= and the TMISSPAT= options are used in determining the number of missing patterns to display. The missing patterns are ordered according to the data proportions they account for, from the largest to the smallest. PROC CALIS displays a minimum number of the highest-frequency missing patterns. This minimum number is the smallest among five, the actual number of missing patterns, and the MAXMISSPAT= value. Then, PROC CALIS displays the subsequent high-frequency missing patterns if the data proportion accounted for by each of these patterns is at least as large as the proportion threshold set by the TMISSPAT= value (default at 0.05) until the total number of missing patterns displayed reaches the maximum set by the MAXMISSPAT= option.
- MEANPATTERN | MEANPAT=name
-
specifies one of the built-in mean structures for the data. The purpose of this option is to fit some commonly-used direct mean structures efficiently without the explicit use of the MSTRUCT model specifications. With this option, the mean structures are defined internally in PROC CALIS. The following names for the built-in mean structures are supported:
- EQMEANVEC
-
specifies the equality of mean vectors between multiple groups. That is, this option tests the null hypothesis that

where
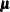 is a common mean vector for the
is a common mean vector for the 
 ’s (
’s ( ). The elements of
). The elements of 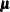 are named _mean_xx automatically by PROC CALIS, where xx represents the row number. For example, if there are four variables in the analysis, the common
are named _mean_xx automatically by PROC CALIS, where xx represents the row number. For example, if there are four variables in the analysis, the common 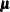 is defined as:
is defined as: 
If you use the COVPATTERN=EQCOVMAT and MEANPATTERN= EQMEANVEC together in a maximum likelihood (METHOD=ML) analysis, you are testing a null hypothesis of the same multivariate normal distribution for the groups.
If you use the MEANPATTERN=EQMEANVEC option for a single-group analysis, the parameters for the single group are still created accordingly. However, the mean model for the single group contains only unconstrained parameters that would result in saturated mean structures for the model.
- SATURATED
-
specifies a saturated mean structure model. This is the default mean structure pattern when the covariance structures are specified by the COVPATTERN= pattern and the mean structure analysis is invoked by MEANSTR option. The elements of
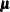 are named _mean_xx automatically by PROC CALIS, where xx represents the row number. For example, if there are three variables in the analysis,
are named _mean_xx automatically by PROC CALIS, where xx represents the row number. For example, if there are three variables in the analysis, 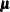 is defined as:
is defined as: 
- UNIFORM
-
specifies a mean vector with a uniform mean parameter _meanparm. For example, if there are three variables in the analysis, the mean pattern generated by PROC CALIS is

- ZERO
-
specifies a zero vector for the mean structures. For example, if there are four variables in the analysis, the mean pattern generated by PROC CALIS is:

When you specify the mean structure model by means of the MEANPATTERN= option, you can define the set of variables in the analysis by the VAR statement (either within the scope of the PROC CALIS statement or the GROUP statements). If the VAR statement is not used, PROC CALIS uses all numerical variables in the data sets.
Except for the EQMEANVEC pattern, all other built-in mean patterns are primarily designed for single-group analysis. However, you can still use these mean pattern options for multiple-group situations. For example, consider the following three-group analysis:
proc calis meanpattern=uniform; group 1 / data=set1; group 2 / data=set2; group 3 / data=set3; run;
In this specification, all three groups are fitted by the uniform mean pattern. However, there would be no constraints across these groups. PROC CALIS generates a distinct mean parameter for each group: _meanparm_mdl1 for Group 1, _meanparm_mdl2 for Group 2, and _meanparm_mdl3 for Group 3. Similarly, the _mdlxx suffix, where xx represents the model number, is applied to the parameters defined by the SATURATED mean pattern in multiple-group situations.
You can also apply the MEANPATTERN= option partially to the groups in the analysis. For example, the following statements apply the ZERO mean pattern to Group 1 and Group 2 only:
proc calis meanpattern=zero; group 1 / data=set1; group 2 / data=set2; group 3 / data=set3; model 3 / group=3; path x1 ---> y3; means x1 = mean_x1; run;Group 3 is fitted by Model 3, which is specified explicitly by a PATH model with a distinct mean parameter mean_x1.
If the EQMEANVEC pattern is specified instead, as shown in the following statements, the equality of mean vectors still holds for Groups 1 and 2:
proc calis meanpattern=eqmeanvec; group 1 / data=set1; group 2 / data=set2; group 3 / data=set3; model 3 / group=3; path x1 ---> y3; means x1 = mean_x1; run;However, Group 3 has it own mean structures as specified in Model 3.
Use the COVPATTERN= option if you also want to analyze some built-in covariance structures along with the mean structures. If you use the MEANPATTERN= option but do not specify the COVPATTERN= option, a saturated covariance structure model (that is, COVPATTERN=SATURATED) is assumed by default.
- MEANSTR
invokes the analysis of mean structures. By default, no mean structures are analyzed. You can specify the MEANSTR option in both the PROC CALIS and the MODEL statements. When this option is specified in the PROC CALIS statement, it propagates to all models. When this option is specified in the MODEL statement, it applies only to the local model. Except for the COSAN model, the MEANSTR option adds default mean parameters to the model. For the COSAN model, the MEANSTR option adds null mean vectors to the model. Instead of using the MEANSTR option to analyze the mean structures, you can specify the mean and the intercept parameters explicitly in the model by some model specification statements. That is, you can specify the intercepts in the LINEQS statement, the intercepts and means in the PATH or the MEAN statement, the _MEAN_ matrix in the MATRIX statement, or the mean structure formula in the COSAN statement. The explicit mean structure parameter specifications are useful when you need to constrain the mean parameters or to create your own references of the parameters.
- METHOD | MET | M=name
-
specifies the method of parameter estimation. The default is METHOD=ML. Valid values for name are as follows:
- FIML
performs full information maximum-likelihood parameter estimation for data with missing values. This method assumes raw input data sets. Exploratory factor analysis and model modification indices are not available with FIML in this version of PROC CALIS. If METHOD=FIML is specified with exploratory factor models, ML is used instead.
- ML | M | MAX
performs normal-theory maximum-likelihood parameter estimation. The ML method requires a nonsingular covariance or correlation matrix.
- GLS | G
performs generalized least squares parameter estimation. If no INWGT= data set is specified, the GLS method uses the inverse sample covariance or correlation matrix as the weight matrix
 . Therefore, METHOD=GLS requires a nonsingular covariance or correlation matrix.
. Therefore, METHOD=GLS requires a nonsingular covariance or correlation matrix. - WLS | W | ADF
performs weighted least squares parameter estimation. If no INWGT= data set is specified, the WLS method uses the inverse matrix of estimated asymptotic covariances of the sample covariance or correlation matrix as the weight matrix
 . In this case, the WLS estimation method is equivalent to Browne’s asymptotically distribution-free estimation (Browne; 1982, 1984). The WLS method requires a nonsingular weight matrix.
. In this case, the WLS estimation method is equivalent to Browne’s asymptotically distribution-free estimation (Browne; 1982, 1984). The WLS method requires a nonsingular weight matrix. - DWLS | D
performs diagonally weighted least squares parameter estimation. If no INWGT= data set is specified, the DWLS method uses the inverse diagonal matrix of asymptotic variances of the input sample covariance or correlation matrix as the weight matrix
 . The DWLS method requires a nonsingular diagonal weight matrix.
. The DWLS method requires a nonsingular diagonal weight matrix. - ULS | LS | U
performs unweighted least squares parameter estimation.
- LSFIML
performs unweighted least squares followed by full information maximum-likelihood parameter estimation.
- LSML | LSM | LSMAX
performs unweighted least squares followed by normal-theory maximum-likelihood parameter estimation.
- LSGLS | LSG
performs unweighted least squares followed by generalized least squares parameter estimation.
- LSWLS | LSW | LSADF
performs unweighted least squares followed by weighted least squares parameter estimation.
- LSDWLS | LSD
performs unweighted least squares followed by diagonally weighted least squares parameter estimation.
- NONE | NO
uses no estimation method. This option is suitable for checking the validity of the input information and for displaying the model matrices and initial values.
- MODIFICATION | MOD
-
computes and displays Lagrange multiplier (LM) test indices for constant parameter constraints, equality parameter constraints, and active boundary constraints, as well as univariate and multivariate Wald test indices. The modification indices are not computed in the case of unweighted or diagonally weighted least squares estimation.
The Lagrange multiplier test (Bentler; 1986; Lee; 1985; Buse; 1982) provides an estimate of the
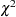 reduction that results from dropping the constraint. For constant parameter constraints and active boundary constraints, the approximate change of the parameter value is displayed also. You can use this value to obtain an initial value if the parameter is allowed to vary in a modified model. See the section Modification Indices for more information.
reduction that results from dropping the constraint. For constant parameter constraints and active boundary constraints, the approximate change of the parameter value is displayed also. You can use this value to obtain an initial value if the parameter is allowed to vary in a modified model. See the section Modification Indices for more information. Relying solely on the LM tests to modify your model can lead to unreliable models that capitalize purely on sampling errors. See MacCallum, Roznowski, and Necowitz (1992) for the use of LM tests.
- MSINGULAR | MSING=r
-
specifies a relative singularity criterion r (r
 ) for the inversion of the information matrix, which is needed to compute the covariance matrix. If you do not specify the SINGULAR= option, the default value for r or MSING= is 1E
) for the inversion of the information matrix, which is needed to compute the covariance matrix. If you do not specify the SINGULAR= option, the default value for r or MSING= is 1E 12; otherwise, the default value is 1E
12; otherwise, the default value is 1E 4
4  SING, where SING is the specified SINGULAR= value.
SING, where SING is the specified SINGULAR= value. When inverting the information matrix, the following singularity criterion is used for the diagonal pivot
 of the matrix:
of the matrix: 
where ASING and VSING are the specified values of the ASINGULAR= and VSINGULAR= options, respectively, and
 is the
is the 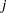 -th diagonal element of the information matrix. Note that in many cases a normalized matrix
-th diagonal element of the information matrix. Note that in many cases a normalized matrix 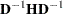 is decomposed (where
is decomposed (where  ), and the singularity criteria are modified correspondingly.
), and the singularity criteria are modified correspondingly. - NOADJDF
turns off the automatic adjustment of degrees of freedom when there are active constraints in the analysis. When the adjustment is in effect, most fit statistics and the associated probability levels will be affected. This option should be used when you believe that the active constraints observed in the current sample will have little chance to occur in repeated sampling. See the section Adjustment of Degrees of Freedom for more discussion on the issue.
- NOBS=nobs
specifies the number of observations. If the DATA= input data set is a raw data set, nobs is defined by default to be the number of observations in the raw data set. The NOBS= and EDF= options override this default definition. You can use the RDF= option to modify the nobs specification. If the DATA= input data set contains a covariance, correlation, or scalar product matrix, you can specify the number of observations either by using the NOBS=, EDF=, and RDF= options in the PROC CALIS statement or by including a _TYPE_='N' observation in the DATA= input data set.
- NOINDEXTYPE
disables the display of index types in the fit summary table.
- NOMEANSTR
-
deactivates the inherited MEANSTR option for the analysis of mean structures. You can specify the NOMEANSTR option in both the PROC CALIS and the MODEL statements. When this option is specified in the PROC CALIS statement, it does not have any apparent effect because by default the mean structures are not analyzed. When this option is specified in the MODEL statement, it deactivates the inherited MEANSTR option from the PROC CALIS statement. In other words, this option is mainly used for resetting the default behavior in the local model that is specified within the scope of a particular MODEL statement. If you specify both the MEANSTR and NOMEANSTR options in the same statement, the NOMEANSTR option is ignored.
Caution: This option does not remove the mean structure specifications from the model. It only deactivates the MEANSTR option inherited from the PROC CALIS statement. The mean structures of the model are analyzed as long as there are mean structure specifications in the model (for example, when you specify the means or intercepts in any of the main or subsidiary model specification statements).
- NOMISSPAT
suppresses the display of the analytic results of the missing patterns. This option is relevant only when there are incomplete observations (with some missing values in the analysis variables) in the input raw data set and when you use METHOD=FIML or METHOD=LSFIML for estimation.
- NOMOD
suppresses the computation of modification indices. The NOMOD option is useful in connection with the PALL option because it saves computing time.
- NOORDERSPEC
prints the model results in the order they appear in the input specifications. This is the default printing behavior. In contrast, the ORDERSPEC option arranges the model results by the types of parameters. You can specify the NOORDERSPEC option in both the PROC CALIS and the MODEL statements. When this option is specified in the PROC CALIS statement, it does not have any apparent effect because by default the model results display in the same order as that in the input specifications. When this option is specified in the MODEL statement, it deactivates the inherited ORDERSPEC option from the PROC CALIS statement. In other words, this option is mainly used for resetting the default behavior in the local model that is specified within the scope of a particular MODEL statement. If you specify both the ORDERSPEC and NOORDERSPEC options in the same statement, the NOORDERSPEC option is ignored.
- NOPARMNAME
suppresses the printing of parameter names in the model results. The default is to print the parameter names. You can specify the NOPARMNAME option in both the PROC CALIS and the MODEL statements. When this option is specified in the PROC CALIS statement, it propagates to all models. When this option is specified in the MODEL statement, it applies only to the local model.
- NOPRINT | NOP
suppresses the displayed output. Note that this option temporarily disables the Output Delivery System (ODS). See Chapter 20, Using the Output Delivery System, for more information.
- NOSTAND
suppresses the printing of standardized results. The default is to print the standardized results.
- NOSTDERR | NOSE
suppresses the printing of the standard error estimates. Standard errors are not computed for unweighted least squares (ULS) or diagonally weighted least squares (DWLS) estimation. In general, standard errors are computed even if the STDERR display option is not used (for file output). You can specify the NOSTDERR option in both the PROC CALIS and the MODEL statements. When this option is specified in the PROC CALIS statement, it propagates to all models. When this option is specified in the MODEL statement, it applies only to the local model.
- OMETHOD | OM=name
- TECHNIQUE | TECH=name
-
specifies the optimization method or technique. Because there is no single nonlinear optimization algorithm available that is clearly superior (in terms of stability, speed, and memory) for all applications, different types of optimization methods or techniques are provided in the CALIS procedure. The optimization method or technique is specified by using one of the following names in the OMETHOD= option:
- CONGRA | CG
chooses one of four different conjugate-gradient optimization algorithms, which can be more precisely defined with the UPDATE= option and modified with the LINESEARCH= option. The conjugate-gradient techniques need only
 memory compared to the
memory compared to the  memory for the other three techniques, where
memory for the other three techniques, where  is the number of parameters. On the other hand, the conjugate-gradient techniques are significantly slower than other optimization techniques and should be used only when memory is insufficient for more efficient techniques. When you choose this option, UPDATE=PB by default. This is the default optimization technique if there are more than 999 parameters to estimate.
is the number of parameters. On the other hand, the conjugate-gradient techniques are significantly slower than other optimization techniques and should be used only when memory is insufficient for more efficient techniques. When you choose this option, UPDATE=PB by default. This is the default optimization technique if there are more than 999 parameters to estimate. - DBLDOG | DD
performs a version of double dogleg optimization, which uses the gradient to update an approximation of the Cholesky factor of the Hessian. This technique is, in many aspects, very similar to the dual quasi-Newton method, but it does not use line search. The implementation is based on Dennis and Mei (1979) and (Gay; 1983).
- LEVMAR | LM | MARQUARDT
performs a highly stable (but for large problems, memory- and time-consuming) Levenberg-Marquardt optimization technique, a slightly improved variant of the (Moré; 1978) implementation. This is the default optimization technique for estimation methods other than the FIML if there are fewer than 500 parameters to estimate.
- NEWRAP | NRA
performs a usually stable (but for large problems, memory- and time-consuming) Newton-Raphson optimization technique. The algorithm combines a line-search algorithm with ridging, and it can be modified with the LINESEARCH= option.
- NRRIDG | NRR | NR | NEWTON
performs a usually stable (but for large problems, memory- and time-consuming) Newton-Raphson optimization technique. This algorithm does not perform a line search. Since OMETHOD=NRRIDG uses an orthogonal decomposition of the approximate Hessian, each iteration of OMETHOD=NRRIDG can be slower than that of OMETHOD=NEWRAP, which works with Cholesky decomposition. However, usually OMETHOD=NRRIDG needs fewer iterations than OMETHOD=NEWRAP. The NRRIDG technique is the default optimization for the FIML estimation if there are fewer than 500 parameters to estimate.
- QUANEW | QN
chooses one of four different quasi-Newton optimization algorithms that can be more precisely defined with the UPDATE= option and modified with the LINESEARCH= option. If boundary constraints are used, these techniques sometimes converge slowly. When you choose this option, UPDATE=DBFGS by default. If nonlinear constraints are specified in the NLINCON statement, a modification of Powell’s VMCWD algorithm (Powell; 1982a, 1982b) is used, which is a sequential quadratic programming (SQP) method. This algorithm can be modified by specifying VERSION=1, which replaces the update of the Lagrange multiplier estimate vector
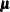 to the original update of Powell (1978b, 1978a) that is used in the VF02AD algorithm. This can be helpful for applications with linearly dependent active constraints. The QUANEW technique is the default optimization technique if there are nonlinear constraints specified or if there are more than 499 and fewer than 1,000 parameters to estimate. The QUANEW algorithm uses only first-order derivatives of the objective function and, if available, of the nonlinear constraint functions.
to the original update of Powell (1978b, 1978a) that is used in the VF02AD algorithm. This can be helpful for applications with linearly dependent active constraints. The QUANEW technique is the default optimization technique if there are nonlinear constraints specified or if there are more than 499 and fewer than 1,000 parameters to estimate. The QUANEW algorithm uses only first-order derivatives of the objective function and, if available, of the nonlinear constraint functions. - TRUREG | TR
performs a usually very stable (but for large problems, memory- and time-consuming) trust-region optimization technique. The algorithm is implemented similar to Gay (1983) and Moré and Sorensen (1983).
- NONE | NO
does not perform any optimization. This option is similar to METHOD=NONE, but OMETHOD=NONE also computes and displays residuals and goodness-of-fit statistics. If you specify METHOD=ML, METHOD=LSML, METHOD=GLS, METHOD=LSGLS, METHOD=WLS, or METHOD=LSWLS, this option enables computing and displaying (if the display options are specified) of the standard error estimates and modification indices corresponding to the input parameter estimates.
For fewer than 500 parameters (
 ), OMETHOD=NRRIDG (Newton-Raphson Ridge) is the default optimization technique for the FIML estimation, and OMETHOD=LEVMAR (Levenberg-Marquardt) is the default optimization technique for the all other estimation methods. For
), OMETHOD=NRRIDG (Newton-Raphson Ridge) is the default optimization technique for the FIML estimation, and OMETHOD=LEVMAR (Levenberg-Marquardt) is the default optimization technique for the all other estimation methods. For  , OMETHOD=QUANEW (quasi-Newton) is the default method, and for
, OMETHOD=QUANEW (quasi-Newton) is the default method, and for  , OMETHOD=CONGRA (conjugate gradient) is the default method. Each optimization method or technique can be modified in various ways. See the section Use of Optimization Techniques for more details.
, OMETHOD=CONGRA (conjugate gradient) is the default method. Each optimization method or technique can be modified in various ways. See the section Use of Optimization Techniques for more details. - ORDERALL
prints the model and group results in the order of the model or group numbers, starting from the smallest number. It also arrange some model results by the parameter types. In effect, this option turns on the ORDERGROUPS, ORDERMODELS, and ORDERSPEC options. The ORDERALL is not a default option. By default, the printing of the results follow the order of the input specifications.
- ORDERGROUPS | ORDERG
prints the group results in the order of the group numbers, starting from the smallest number. The default behavior, however, is to print the group results in the order they appear in the input specifications.
- ORDERMODELS | ORDERMO
prints the model results in the order of the model numbers, starting from the smallest number. The default behavior, however, is to print the model results in the order they appear in the input specifications.
- ORDERSPEC
arranges some model results by the types of parameters. The default behavior, however, is to print the results in the order they appear in the input specifications. You can specify the ORDERSPEC option in both the PROC CALIS and the MODEL statements. When this option is specified in the PROC CALIS statement, it propagates to all models. When this option is specified in the MODEL statement, it applies only to the local model.
- OUTEST=SAS-data-set
-
creates an output data set that contains the parameter estimates, their gradient, Hessian matrix, and boundary and linear constraints. For METHOD=ML, METHOD=GLS, and METHOD=WLS, the OUTEST= data set also contains the information matrix, the approximate covariance matrix of the parameter estimates ((generalized) inverse of information matrix), and approximate standard errors. If linear or nonlinear equality or active inequality constraints are present, the Lagrange multiplier estimates of the active constraints, the projected Hessian, and the Hessian of the Lagrange function are written to the data set.
See the section OUTEST= SAS-data-set for a description of the OUTEST= data set. If you want to create a permanent SAS data set, you must specify a two-level name. Refer to the chapter titled "SAS Data Files" in SAS Language Reference: Concepts for more information about permanent data sets.
- OUTFIT=SAS-data-set
creates an output data set that contains the values of the fit indices. See the section OUTFIT= SAS-data-set for details.
- OUTMODEL | OUTRAM=SAS-data-set
-
creates an output data set that contains the model information for the analysis, the parameter estimates, and their standard errors. An OUTMODEL= data set can be used as an input INMODEL= data set in a subsequent analysis by PROC CALIS. The OUTMODEL= data set also contains a set of fit indices; the section OUTMODEL= SAS-data-set provides more details. If you want to create a permanent SAS data set, you must specify a two-level name.
Refer to the chapter titled "SAS Data Files" in SAS Language Reference: Concepts for more information about permanent data sets.
- OUTSTAT=SAS-data-set
-
creates an output data set that contains the BY group variables, the analyzed covariance or correlation matrices, and the predicted and residual covariance or correlation matrices of the analysis. You can specify the correlation or covariance matrix in an OUTSTAT= data set as an input DATA= data set in a subsequent analysis by PROC CALIS. See the section OUTSTAT= SAS-data-set for a description of the OUTSTAT= data set. If the model contains latent variables, this data set also contains the predicted covariances between latent and manifest variables and the latent variable score regression coefficients (see the PLATCOV option). If the FACTOR statement is used, the OUTSTAT= data set also contains the rotated and unrotated factor loadings, the unique variances, the matrix of factor correlations, the transformation matrix of the rotation, and the matrix of standardized factor loadings.
You can use the latent variable score regression coefficients with PROC SCORE to compute factor scores.
If you want to create a permanent SAS data set, you must specify a two-level name.
Refer to the chapter titled "SAS Data Files" in SAS Language Reference: Concepts for more information about permanent data sets.
- OUTWGT | OUTWEIGHT=SAS-data-set
-
creates an output data set that contains the elements of the weight matrix
 or the its inverse
or the its inverse  used in the estimation process. The inverse of the weight matrix is output only when you specify an INWGT= data set with the INWGT= and INWGTINV options (or the INWGT(INV)= option alone) in the same analysis. As a result, the entries in the INWGT= and OUTWGT= data sets are consistent. In other situations where the weight matrix is computed by the procedure or obtained from the OUTWGT= data set without the INWGTINV option, the weight matrix is output in the OUTWGT= data set. Furthermore, if the weight matrix is computed by the procedure, the OUTWGT= data set contains the elements of the weight matrix on which the WRIDGE= and the WPENALTY= options are applied.
used in the estimation process. The inverse of the weight matrix is output only when you specify an INWGT= data set with the INWGT= and INWGTINV options (or the INWGT(INV)= option alone) in the same analysis. As a result, the entries in the INWGT= and OUTWGT= data sets are consistent. In other situations where the weight matrix is computed by the procedure or obtained from the OUTWGT= data set without the INWGTINV option, the weight matrix is output in the OUTWGT= data set. Furthermore, if the weight matrix is computed by the procedure, the OUTWGT= data set contains the elements of the weight matrix on which the WRIDGE= and the WPENALTY= options are applied. You cannot create an OUTWGT= data set with an unweighted least squares or maximum likelihood estimation. The weight matrix is defined only in the GLS, WLS (ADF), or DWLS fit function. An OUTWGT= data set can be used as an input INWGT= data set in a subsequent analysis by PROC CALIS. See the section OUTWGT= SAS-data-set for the description of the OUTWGT= data set. If you want to create a permanent SAS data set, you must specify a two-level name.
Refer to the chapter titled "SAS Data Files" in SAS Language Reference: Concepts for more information about permanent data sets.
- PALL | ALL
-
displays all optional output except the output generated by the PCOVES and PDETERM options.
Caution: The PALL option includes the very expensive computation of the modification indices. If you do not really need modification indices, you can save computing time by specifying the NOMOD option in addition to the PALL option.
- PARMNAME
prints the parameter names in the model results. This is the default printing behavior. In contrast, the NOPARMNAME option suppresses the printing of the parameter names in the model results. You can specify the PARMNAME option in both the PROC CALIS and the MODEL statements. When this option is specified in the PROC CALIS statement, it does not have any apparent effect because by default model results show the parameter names. When this option is specified in the MODEL statement, it deactivates the inherited NOPARMNAME option from the PROC CALIS statement. In other words, this option is mainly used for resetting the default behavior in the local model that is specified within the scope of a particular MODEL statement. If you specify both the PARMNAME and NOPARMNAME options in the same statement, the PARMNAME option is ignored.
- PCORR | CORR
displays the covariance or correlation matrix that is analyzed and the predicted model covariance or correlation matrix.
- PCOVES | PCE
-
the information matrix
the approximate covariance matrix of the parameter estimates (generalized inverse of the information matrix)
the approximate correlation matrix of the parameter estimates
The covariance matrix of the parameter estimates is not computed for estimation methods ULS and DWLS. This displayed output is not included in the output generated by the PALL option.
- PDETERM | PDE
-
displays three coefficients of determination: the determination of all equations (DETAE), the determination of the structural equations (DETSE), and the determination of the manifest variable equations (DETMV). These determination coefficients are intended to be global means of the squared multiple correlations for different subsets of model equations and variables. The coefficients are displayed only when you specify a FACTOR, LINEQS, LISMOD, PATH, or RAM model, but they are displayed for all five estimation methods: ULS, GLS, ML, WLS, and DWLS.
You can use the STRUCTEQ statement to define which equations are structural equations. If you do not use the STRUCTEQ statement, PROC CALIS uses its own default definition to identify structural equations.
The term "structural equation" is not defined in a unique way. The LISREL program defines the structural equations by the user-defined BETA matrix. In PROC CALIS, the default definition of a structural equation is an equation that has a dependent left-side variable that appears at least once on the right side of another equation, or an equation that has at least one right-side variable that appears at the left side of another equation. Therefore, PROC CALIS sometimes identifies more equations as structural equations than the LISREL program does.
- PESTIM | PES
displays the parameter estimates. In some cases, this includes displaying the standard errors and
 values.
values. - PINITIAL | PIN
displays the model specification with initial estimates and the vector of initial values.
- PLATCOV | PLATMOM | PLC
-
the estimates of the covariances among the latent variables
the estimates of the covariances between latent and manifest variables
the estimates of the latent variable means for mean structure analysis
the latent variable score regression coefficients
The estimated covariances between latent and manifest variables and the latent variable score regression coefficients are written to the OUTSTAT= data set. You can use the score coefficients with PROC SCORE to compute factor scores.
- PLOTS | PLOT < = plot-request>
- PLOTS | PLOT < = ( plot-request < ...plot-request> ) >
-
specifies the ODS graphical plots. Currently, the only available ODS graphical plots in PROC CALIS are for residual histograms. Also, when the residual histograms are requested, the bar charts of residual tallies are suppressed. To display these bar charts with the residual histograms, you must use the RESIDUAL(TALLY) option.
When you specify only one plot-request, you can omit the parentheses around the plot-request. For example:
PLOTS=ALL
PLOTS=RESIDUALS
ODS Graphics must be enabled before requesting plots. For example:ods graphics on; proc calis plots; path y <--- x, y <--- z; run; ods graphics off;For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21, Statistical Graphics Using ODS.
The following table shows the available plot-requests:
Plot-request
Plot Description
ALL
All available plots
NONE
No ODS graphical plots
RESIDUALS
Distribution of residuals
- PRIMAT | PMAT
displays parameter estimates, approximate standard errors, and
 values in matrix form if you specify the analysis model using the RAM or LINEQS statement.
values in matrix form if you specify the analysis model using the RAM or LINEQS statement. - PRINT | PRI
adds the options KURTOSIS, RESIDUAL, PLATCOV, and TOTEFF to the default output.
- PSHORT | SHORT | PSH
excludes the output produced by the PINITIAL, SIMPLE, and STDERR options from the default output.
- PSUMMARY | SUMMARY | PSUM
- PWEIGHT | PW
displays the weight matrix
 used in the estimation. The weight matrix is displayed after the WRIDGE= and the WPENALTY= options are applied to it. However, if you specify an INWGT= data set by the INWGT= and INWGTINV options (or the INWGT(INV)= option alone) in the same analysis, this option displays the elements of the inverse of the weight matrix.
used in the estimation. The weight matrix is displayed after the WRIDGE= and the WPENALTY= options are applied to it. However, if you specify an INWGT= data set by the INWGT= and INWGTINV options (or the INWGT(INV)= option alone) in the same analysis, this option displays the elements of the inverse of the weight matrix. - RADIUS=r
is an alias for the INSTEP= option for Levenberg-Marquardt minimization.
- RANDOM=i
specifies a positive integer as a seed value for the pseudo-random number generator to generate initial values for the parameter estimates for which no other initial value assignments in the model definitions are made. Except for the parameters in the diagonal locations of the central matrices in the model, the initial values are set to random numbers in the range
 . The values for parameters in the diagonals of the central matrices are random numbers multiplied by
. The values for parameters in the diagonals of the central matrices are random numbers multiplied by  or
or  . See the section Initial Estimates for more information.
. See the section Initial Estimates for more information. - RDF | DFR=n
makes the effective number of observations the actual number of observations minus the RDF= value. The degree of freedom for the intercept should not be included in the RDF= option. If you use PROC CALIS to compute a regression model, you can specify RDF= number-of-regressor-variables to get approximate standard errors equal to those computed by PROC REG.
- READADDPARM | READADD
inputs the generated default parameters (for example, observations with _TYPE_=ADDPCOV, ADDMEAN, or ADDPVAR) in the INMODEL= data set as if they were part of the original model specification. Typically, these default parameters in the INMODEL= data set were generated automatically by PROC CALIS in a previous analysis and stored in an OUTMODEL= data set, which is then used as the INMODEL= data set in a new run of PROC CALIS. By default, PROC CALIS does not input the observations for default parameters in the INMODEL= data set. In most applications, you do not need to specify this option because PROC CALIS is able to generate a new set of default parameters that are appropriate to the new situation after it reads in the INMODEL= data set. Undistinguished uses of the READADDPARM option might lead to unintended constraints on the default parameters.
- RESIDUAL | RES <(TALLY | TALLIES)> < = NORM | VARSTAND | ASYSTAND>
-
displays the raw and normalized residual covariance matrix, the rank order of the largest residuals, and a bar chart of the residual tallies. This information is displayed by default when you specify the PRINT option.
Three types of normalized or standardized residual matrices can be chosen with the RESIDUAL= specification.
- RESIDUAL= NORM
normalized residuals
- RESIDUAL= VARSTAND
variance standardized residuals
- RESIDUAL= ASYSTAND
asymptotically standardized residuals
When ODS graphical plots of residuals are also requested, the bar charts of residual tallies are suppressed. They are replaced with high quality graphical histograms showing residual distributions. If you still want to display the bar charts in this situation, use the RESIDUAL(TALLY) or RESIDUAL(TALLY)= option.
See the section Assessment of Fit for more details.
- RIDGE<=r>
-
defines a ridge factor r for the diagonal of the covariance or correlation matrix
 that is analyzed. The matrix
that is analyzed. The matrix  is transformed to:
is transformed to: 
If you do not specify r in the RIDGE option, PROC CALIS tries to ridge the covariance or correlation matrix
 so that the smallest eigenvalue is about
so that the smallest eigenvalue is about  . Because the weight matrix in the GLS method is the same as the observed covariance or correlation matrix, the RIDGE= option also applies to the weight matrix for the GLS estimation, unless you input the weight matrix by the INWGT= option.
. Because the weight matrix in the GLS method is the same as the observed covariance or correlation matrix, the RIDGE= option also applies to the weight matrix for the GLS estimation, unless you input the weight matrix by the INWGT= option. Caution: The covariance or correlation matrix in the OUTSTAT= output data set does not contain the ridged diagonal.
- SALPHA=r
is an alias for the INSTEP= option for line-search algorithms.
- SIMPLE | S
displays means, standard deviations, skewness, and univariate kurtosis if available. This information is displayed when you specify the PRINT option. If the KURTOSIS option is specified, the SIMPLE option is set by default.
- SINGULAR | SING =r
specifies the singularity criterion r (
 r
r  ) used, for example, for matrix inversion. The default value is the square root of the relative machine precision or, equivalently, the square root of the largest double precision value that, when added to 1, results in 1.
) used, for example, for matrix inversion. The default value is the square root of the relative machine precision or, equivalently, the square root of the largest double precision value that, when added to 1, results in 1. - SLMW=r
specifies the probability limit used for computing the stepwise multivariate Wald test. The process stops when the univariate probability is smaller than r. The default value is r
 .
. - SPRECISION | SP=r
is an alias for the LSPRECISION= option.
- START=r
specifies initial estimates for parameters as multiples of the r value. In all CALIS models, you can supply initial estimates individually as parenthesized values after each parameter name. Unspecified initial estimates are usually computed by various reasonable initial estimation methods in PROC CALIS. If none of the initialization methods is able to compute all the unspecified initial estimates, then the remaining unspecified initial estimates are set to r,
 r
r , or
, or  r
r . For variance parameters,
. For variance parameters,  is used for covariance structure analyses and
is used for covariance structure analyses and  r
r is used for correlation structure analyses. For other types of parameters, r is used. The default value is r
is used for correlation structure analyses. For other types of parameters, r is used. The default value is r . If the DEMPHAS= option is used, the initial values of the variance parameters are multiplied by the value specified in the DEMPHAS= option. See the section Initial Estimates for more information.
. If the DEMPHAS= option is used, the initial values of the variance parameters are multiplied by the value specified in the DEMPHAS= option. See the section Initial Estimates for more information. - STDERR | SE
-
displays approximate standard errors if estimation methods other than unweighted least squares (ULS) or diagonally weighted least squares (DWLS) are used (and the NOSTDERR option is not specified). In contrast, the NOSTDERR option suppresses the printing of the standard error estimates. If you specify neither the STDERR nor the NOSTDERR option, the standard errors are computed for the OUTMODEL= data set. This information is displayed by default when you specify the PRINT option.
You can specify the STDERR option in both the PROC CALIS and the MODEL statements. When this option is specified in the PROC CALIS statement, it does not have any apparent effect because by default the model results display the standard error estimates (for estimation methods other than ULS and DWLS). When this option is specified in the MODEL statement, it deactivates the inherited NOSTDERR or NOSE option from the PROC CALIS statement. In other words, this option is mainly used for resetting the default behavior in the local model that is specified within the scope of a particular MODEL statement. If you specify both the STDERR and NOSTDERR options in the same statement, the STDERR option is ignored.
- TMISSPAT | THRESHOLDMISSPAT | THRESMISSPAT=n
-
specifies the proportion threshold for the missing patterns to display in the output, where n is between 0 and 1. The default TMISSPAT= value is 0.05. This option is relevant only when there are incomplete observations (with some missing values in the analysis variables) in the input raw data set and when you use METHOD=FIML or METHOD=LSFIML for estimation.
Because the number of missing patterns could be quite large, PROC CALIS displays a limited number of the most frequent missing patterns in the output. Together with the MAXMISSPAT= option, this option controls the number of missing patterns to display in the output. See the MAXMISSPAT= option for a detailed description about how the number of missing patterns to display is determined.
- UPDATE | UPD=name
-
specifies the update method for the quasi-Newton or conjugate-gradient optimization technique.
For OMETHOD=CONGRA, the following updates can be used:
- PB
performs the automatic restart update method of Powell (1977) and Beale (1972). This is the default.
- FR
performs the Fletcher-Reeves update (Fletcher; 1980, p. 63).
- PR
performs the Polak-Ribiere update (Fletcher; 1980, p. 66).
- CD
performs a conjugate-descent update of Fletcher (1987).
For OMETHOD=DBLDOG, the following updates (Fletcher; 1987) can be used:
- DBFGS
performs the dual Broyden, Fletcher, Goldfarb, and Shanno (BFGS) update of the Cholesky factor of the Hessian matrix. This is the default.
- DDFP
performs the dual Davidon, Fletcher, and Powell (DFP) update of the Cholesky factor of the Hessian matrix.
For OMETHOD=QUANEW, the following updates (Fletcher; 1987) can be used:
- BFGS
performs original BFGS update of the inverse Hessian matrix. This is the default for earlier releases.
- DFP
performs the original DFP update of the inverse Hessian matrix.
- DBFGS
performs the dual BFGS update of the Cholesky factor of the Hessian matrix. This is the default.
- DDFP
performs the dual DFP update of the Cholesky factor of the Hessian matrix.
- VARDEF= DF | N | WDF | WEIGHT | WGT
-
specifies the divisor used in the calculation of covariances and standard deviations. The default value is VARDEF=N for the METHOD=FIML, and VARDEF=DF for other estimation methods. The values and associated divisors are displayed in the following table, where
 is the number of partial variables specified in the PARTIAL statement. When a WEIGHT statement is used,
is the number of partial variables specified in the PARTIAL statement. When a WEIGHT statement is used,  is the value of the WEIGHT variable in the
is the value of the WEIGHT variable in the  th observation, and the summation is performed only over observations with positive weight.
th observation, and the summation is performed only over observations with positive weight. Value
Description
Divisor
DF
Degrees of freedom

N
Number of observations
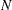
WDF
Sum of weights DF

WEIGHT | WGT
Sum of weights

- VSINGULAR | VSING=r
-
specifies a relative singularity criterion r ( r
 ) for the inversion of the information matrix, which is needed to compute the covariance matrix. If you do not specify the SINGULAR= option, the default value for r or VSING= is 1E
) for the inversion of the information matrix, which is needed to compute the covariance matrix. If you do not specify the SINGULAR= option, the default value for r or VSING= is 1E 8; otherwise, the default value is SING, which is the specified SINGULAR= value.
8; otherwise, the default value is SING, which is the specified SINGULAR= value. When inverting the information matrix, the following singularity criterion is used for the diagonal pivot
 of the matrix:
of the matrix: 
where ASING and MSING are the specified values of the ASINGULAR= and MSINGULAR= options, respectively, and
 is the
is the  -th diagonal element of the information matrix. Note that in many cases a normalized matrix
-th diagonal element of the information matrix. Note that in many cases a normalized matrix 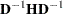 is decomposed (where
is decomposed (where  ), and the singularity criteria are modified correspondingly.
), and the singularity criteria are modified correspondingly. - WPENALTY | WPEN=r
-
specifies the penalty weight
 for the WLS and DWLS fit of the diagonal elements of a correlation matrix (constant 1s). The criterion for weighted least squares estimation of a correlation structure is
for the WLS and DWLS fit of the diagonal elements of a correlation matrix (constant 1s). The criterion for weighted least squares estimation of a correlation structure is 
where r is the penalty weight specified by the WPENALTY=r option and the
 are the elements of the inverse of the reduced
are the elements of the inverse of the reduced  weight matrix that contains only the nonzero rows and columns of the full weight matrix
weight matrix that contains only the nonzero rows and columns of the full weight matrix  . The second term is a penalty term to fit the diagonal elements of the correlation matrix. The default value is 100. The reciprocal of this value replaces the asymptotic variance corresponding to the diagonal elements of a correlation matrix in the weight matrix
. The second term is a penalty term to fit the diagonal elements of the correlation matrix. The default value is 100. The reciprocal of this value replaces the asymptotic variance corresponding to the diagonal elements of a correlation matrix in the weight matrix  , and it is effective only with the ASYCOV=CORR option, which is the default for correlation analyses. The often used value
, and it is effective only with the ASYCOV=CORR option, which is the default for correlation analyses. The often used value 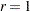 seems to be too small in many cases to fit the diagonal elements of a correlation matrix properly. The default WPENALTY= value emphasizes the importance of the fit of the diagonal elements in the correlation matrix. You can decrease or increase the value of r if you want to decrease or increase the importance of the diagonal elements fit. This option is effective only with the WLS or DWLS estimation method and the analysis of a correlation matrix.
seems to be too small in many cases to fit the diagonal elements of a correlation matrix properly. The default WPENALTY= value emphasizes the importance of the fit of the diagonal elements in the correlation matrix. You can decrease or increase the value of r if you want to decrease or increase the importance of the diagonal elements fit. This option is effective only with the WLS or DWLS estimation method and the analysis of a correlation matrix. See the section Estimation Criteria for more details.
Caution: If you input the weight matrix by the INWGT= option, the WPENALTY= option is ignored.
- WRIDGE=r
-
defines a ridge factor r for the diagonal of the weight matrix
 used in GLS, WLS, or DWLS estimation. The weight matrix
used in GLS, WLS, or DWLS estimation. The weight matrix  is transformed to
is transformed to 
The WRIDGE= option is applied on the weight matrix before the following actions occur:
the WPENALTY= option is applied on it
the weight matrix is written to the OUTWGT= data set
the weight matrix is displayed
Caution: If you input the weight matrix by the INWGT= option, the OUTWGT= data set will contain the same weight matrix without the ridging requested by the WRIDGE= option. This ensures that the entries in the INWGT= and OUTWGT= data sets are consistent. The WRIDGE= option is ignored if you input the inverse of the weight matrix by the INWGT= and INWGTINV options (or the INWGT(INV)= option alone).