In this example, cognitive abilities of 64 students from a middle school were measured. The fictitious data contain nine cognitive test scores. Three of the scores were for reading skills, three others were for math skills, and the remaining three were for writing skills. The covariance matrix for the nine variables was obtained. A confirmatory factor analysis with three factors was conducted. The following is the input data set:
Confirmatory Factor Model with Uncorrelated Factors
You first fit a confirmatory factor model with uncorrelated factors to the data, as shown in the following statements:
proc calis data=cognitive1 nobs=64 modification;
factor
Read_Factor ---> reading1-reading3 ,
Math_Factor ---> math1-math3 ,
Write_Factor ---> writing1-writing3 ;
pvar
Read_Factor Math_Factor Write_Factor = 3 * 1.;
cov
Read_Factor Math_Factor Write_Factor = 3 * 0.;
run;
In the PROC CALIS statement, the number of observations is specified with the NOBS= option. With the MODIFICATION in the PROC CALIS statement, LM (Lagrange Multiplier) tests are conducted. The results of LM tests can suggest the inclusion of additional parameters for a better model fit.
The FACTOR modeling language is most handy when you specify confirmatory factor models. You use the FACTOR statement to invoke the FACTOR modeling language. Entries in the FACTOR statement are for specifying factor-variables relationships and are separated by commas. In each entry, you first specify a latent factor, followed by the right arrow sign ---> (you can use >, ->, -->, or --->). Then you specify the observed variables that have nonzero loadings on the factor. For example, in the first entry of FACTOR statement, you specify that latent factor Read_Factor has nonzero loadings (free parameters) on variables reading1–reading3. Optionally, you can specify the parameter list after you specify the factor-variable relationships. For example, you can name the loading parameters as in the following specification:
factor
Read_Factor ---> reading1-reading3 = load1-load3;
This way, you name the factor loadings with parameter names load1, load2, and load3, respectively. However, in the current example, because the loading parameters are all unconstrained, you can just let PROC CALIS to generate the parameter names for you. In this example, there are three factors: Read_Factor, Math_Factor, and Write_Factor. These factors have simple cluster structures with the nine observed variables. Each observed variable has only one loading on exactly one factor.
In the PVAR statement, you can specify the variances of the factors and the error variances of the observed variables. The factor variances in this model are all fixed at 1.0 for identification purposes. You do not need to specify the error variances of the observed variables in the current model because PROC CALIS assumes these are free parameters by default.
In the COV statement, you specify that the covariances among the factors are fixed zeros. There are three covariances among the three latent factors and therefore you put 3 * 0. for their fixed values. This means that the factors in the current model are uncorrelated. Note that you must specify uncorrelated factors explicitly in the COV statement because all latent factors are correlated by default.
In Output 26.19.1, the initial model specification is echoed in matrix form. The observed variables and factors are also displayed.
Output 26.19.1
Uncorrelated Factor Model Specification
| reading1 reading2 reading3 math1 math2 math3 writing1 writing2 writing3 |
| Read_Factor Math_Factor Write_Factor |
| 1.0000 |
0 |
0 |
| 0 |
1.0000 |
0 |
| 0 |
0 |
1.0000 |
| _Add1 |
. |
| _Add2 |
. |
| _Add3 |
. |
| _Add4 |
. |
| _Add5 |
. |
| _Add6 |
. |
| _Add7 |
. |
| _Add8 |
. |
| _Add9 |
. |
In the table for initial factor loading matrix, the nine loading parameters are shown to have simple cluster relations with the factors. In the table for initial factor covariance matrix, the diagonal matrix shows that the factors are not correlated. The diagonal elements are fixed at ones so that this matrix is also a correlation matrix for the factors. In the table for initial error variances, the nine variance parameters are shown. As described previously, these error variances are generated by PROC CALIS as default parameters.
In Output 26.19.2, initial estimates are generated by the instrumental variable method and the McDonald method.
Output 26.19.2
Optimization of the Uncorrelated Factor Model: Initial Estimates
| 1 |
Instrumental Variables Method |
| 2 |
McDonald Method |
| 7.15372 |
0.00851 |
| 7.80225 |
-0.00170 |
| 8.70856 |
-0.00602 |
| 7.68637 |
0.00272 |
| 8.01765 |
-0.01096 |
| 7.05012 |
0.00932 |
| 8.76776 |
-0.0009955 |
| 5.96161 |
-0.01335 |
| 7.23168 |
0.01665 |
| 31.84831 |
-0.00179 |
| 47.36790 |
0.0003461 |
| 23.50199 |
0.00257 |
| 23.13374 |
-0.0008384 |
| 31.84224 |
0.00280 |
| 38.92075 |
-0.00167 |
| 13.86035 |
-0.00579 |
| 61.00217 |
0.00115 |
| 46.14784 |
-0.00300 |
These initial estimates turn out to be pretty good, in the sense that only three more iterations are needed to converge to the maximum likelihood estimates and the final function value  does not change much from the initial function value
does not change much from the initial function value  , as shown in Output 26.19.3.
, as shown in Output 26.19.3.
Output 26.19.3
Optimization of the Uncorrelated Factor Model: Iteration Summary
| |
0 |
4 |
0 |
|
0.78792 |
0.1225 |
0.00175 |
0 |
0.932 |
| |
0 |
6 |
0 |
|
0.78373 |
0.00419 |
0.000037 |
0 |
1.051 |
| |
0 |
8 |
0 |
|
0.78373 |
5.087E-7 |
3.715E-9 |
0 |
1.001 |
| 3 |
11 |
| 5 |
0 |
| 0.783733415 |
3.7146571E-9 |
| 0 |
1.0006660673 |
| 0.0025042942 |
|
| Convergence criterion (ABSGCONV=0.00001) satisfied. |
The fit summary is shown in Output 26.19.4.
Output 26.19.4
Fit of the Uncorrelated Factor Model
| 64 |
| 9 |
| 45 |
| 18 |
| 0 |
| 4.3182 |
| 272.0467 |
| 36 |
| <.0001 |
| 0.7837 |
| 49.3752 |
| 27 |
| 0.0054 |
| 2.5474 |
| 52 |
| 19.5739 |
| 0.2098 |
| 0.8555 |
| 0.7592 |
| 0.6416 |
| 0.1147 |
| 0.0617 |
| 0.1646 |
| 0.0271 |
| 1.4630 |
| 1.2069 |
| 1.8687 |
| 85.3752 |
| 142.2351 |
| 124.2351 |
| 0.8396 |
| 0.9052 |
| 0.8185 |
| 0.8736 |
| 0.7580 |
| 0.9087 |
| 0.6139 |
Using the chi-square model test criterion, the uncorrelated factor model should be rejected at 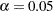 . The RMSEA estimate is
. The RMSEA estimate is 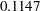 , which is not indicative of a good fit according to Browne and Cudeck (1993) Other indices might suggest only a marginal good fit. For example, Bentler’s comparative fit index and Bollen nonnormed index delta2 are both above 0.90. However, many other do not attain this 0.90 level. For example, adjusted GFI is only
, which is not indicative of a good fit according to Browne and Cudeck (1993) Other indices might suggest only a marginal good fit. For example, Bentler’s comparative fit index and Bollen nonnormed index delta2 are both above 0.90. However, many other do not attain this 0.90 level. For example, adjusted GFI is only 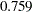 . It is thus safe to conclude that there could be some improvements on the model fit.
. It is thus safe to conclude that there could be some improvements on the model fit.
The MODIFICATION option in the PROC CALIS statement has been used to request for computing the LM test indices for model modifications. The results are shown in Output 26.19.5.
Output 26.19.5
Lagrange Multiplier Tests
| 9.76596 |
0.0018 |
2.95010 |
| 3.58077 |
0.0585 |
1.89703 |
| 2.15312 |
0.1423 |
1.17976 |
| 1.87637 |
0.1707 |
1.41298 |
| 1.02954 |
0.3103 |
0.95427 |
| 0.91230 |
0.3395 |
0.99933 |
| 0.86221 |
0.3531 |
0.95672 |
| 0.63403 |
0.4259 |
0.73916 |
| 0.55602 |
0.4559 |
0.63906 |
| 0.55362 |
0.4568 |
0.74628 |
| 8.95268 |
0.0028 |
0.44165 |
| 7.07904 |
0.0078 |
0.40132 |
| 4.61896 |
0.0316 |
0.30411 |
| 5.45986 |
0.0195 |
-13.16822 |
| 5.05573 |
0.0245 |
12.32431 |
| 3.93014 |
0.0474 |
13.59149 |
| 2.83209 |
0.0924 |
-9.86342 |
| 2.56677 |
0.1091 |
10.15901 |
| 1.94879 |
0.1627 |
8.40273 |
| 1.75181 |
0.1856 |
-7.82777 |
| 1.57978 |
0.2088 |
-7.97915 |
| 1.34894 |
0.2455 |
7.77158 |
| 1.11704 |
0.2906 |
-7.23762 |
Three different tables for ranking the LM test results are shown. In the first table, the new loading parameters that would improve the model fit the most are shown first. For example, in the first row a new factor loading of writing1 on the Read_Factor is suggested to improve the model fit the most. The LM Stat value is  . This is an approximation of the chi-square drop if this parameter was included in the model. The Pr > ChiSq value of
. This is an approximation of the chi-square drop if this parameter was included in the model. The Pr > ChiSq value of  indicates a significant improvement of model fit at
indicates a significant improvement of model fit at 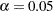 . Nine more new loading parameters are suggested in the table, with less and less statistical significance in the change of model fit chi-square. Note that these approximate chi-squares are one-at-a-time chi-square changes. That means that the overall chi-square drop is not a simple sum of individual chi-square changes when you include two or more new parameters in the modified model.
. Nine more new loading parameters are suggested in the table, with less and less statistical significance in the change of model fit chi-square. Note that these approximate chi-squares are one-at-a-time chi-square changes. That means that the overall chi-square drop is not a simple sum of individual chi-square changes when you include two or more new parameters in the modified model.
The other two tables in Output 26.19.5 shows the new parameters in factor covariances, error variances, or error covariances that would result in a better model fit. The table for the new parameters of the factor covariance matrix indicates that adding each of the covariances among factors might lead to a statistically significant improvement in model fit. The largest LM Stat value in this table is  , which is smaller than that of the largest LM Stat for the factor loading parameters. Despite this, it is more reasonable to add the covariance parameters among factors first to determine whether that improves the model fit.
, which is smaller than that of the largest LM Stat for the factor loading parameters. Despite this, it is more reasonable to add the covariance parameters among factors first to determine whether that improves the model fit.
Confirmatory Factor Model with Correlated Factors
To fit the corresponding confirmatory factor model with correlated factors, you can remove the fixed zeros from the COV statement in the preceding specification, as shown in the following statements:
proc calis data=cognitive1 nobs=64 modification;
factor
Read_Factor ---> reading1-reading3 ,
Math_Factor ---> math1-math3 ,
Write_Factor ---> writing1-writing3 ;
pvar
Read_Factor Math_Factor Write_Factor = 3 * 1.;
cov
Read_Factor Math_Factor Write_Factor /* = 3 * 0. */;
run;
In the COV statement, you comment out the fixed zeros so that the covariances among the latent factors are now free parameters. An alternative way is to delete the entire COV statement so that the covariances among factors are free parameters by the FACTOR model default.
The fit summary of the correlated factor model is shown in Output 26.19.6.
Output 26.19.6
Fit of the Correlated Factor Model
| 64 |
| 9 |
| 45 |
| 21 |
| 0 |
| 4.3182 |
| 272.0467 |
| 36 |
| <.0001 |
| 0.4677 |
| 29.4667 |
| 24 |
| 0.2031 |
| 0.8320 |
| 78 |
| 5.7038 |
| 0.0607 |
| 0.9109 |
| 0.8330 |
| 0.6073 |
| 0.0601 |
| 0.0000 |
| 0.1244 |
| 0.3814 |
| 1.2602 |
| 1.2453 |
| 1.5637 |
| 71.4667 |
| 137.8032 |
| 116.8032 |
| 0.9582 |
| 0.9768 |
| 0.8917 |
| 0.9653 |
| 0.8375 |
| 0.9780 |
| 0.5945 |
The model fit chi-square value is 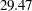 , which is about
, which is about  less than the model with uncorrelated factors. The
less than the model with uncorrelated factors. The 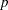 -value is
-value is  , indicating a satisfactory model fit. The RMSEA value is
, indicating a satisfactory model fit. The RMSEA value is  , which is close to
, which is close to  , a value recommended as an indication of good model fit by Browne and Cudeck (1993) More fit indices that do not attain the
, a value recommended as an indication of good model fit by Browne and Cudeck (1993) More fit indices that do not attain the  level with the uncorrelated factor model now have values close to or above
level with the uncorrelated factor model now have values close to or above  . These include the goodness-of-fit index (GFI), McDonald centrality, Bentler-Bonnet NFI, and Bentler-Bonnet nonnormed index. By all counts, the correlated factor model is a much better fit than the uncorrelated factor model.
. These include the goodness-of-fit index (GFI), McDonald centrality, Bentler-Bonnet NFI, and Bentler-Bonnet nonnormed index. By all counts, the correlated factor model is a much better fit than the uncorrelated factor model.
In Output 26.19.7, the estimation results for factor loadings are shown. All these loadings are statistically significant, indicating non-chance relationships with the factors.
Output 26.19.7
Estimation of the Factor Loading Matrix
| 6.7657 |
| 1.0459 |
| 6.4689 |
| [_Parm01] |
|
|
|
| 7.8579 |
| 1.1890 |
| 6.6090 |
| [_Parm02] |
|
|
|
| 9.1344 |
| 1.0712 |
| 8.5269 |
| [_Parm03] |
|
|
|
|
| 7.5488 |
| 1.0128 |
| 7.4536 |
| [_Parm04] |
|
|
|
| 8.4401 |
| 1.0838 |
| 7.7874 |
| [_Parm05] |
|
|
|
| 6.8194 |
| 1.0910 |
| 6.2506 |
| [_Parm06] |
|
|
|
|
| 7.9677 |
| 1.1254 |
| 7.0797 |
| [_Parm07] |
|
|
|
| 6.8742 |
| 1.1986 |
| 5.7350 |
| [_Parm08] |
|
|
|
| 7.0949 |
| 1.2057 |
| 5.8844 |
| [_Parm09] |
|
In Output 26.19.8, the factor covariance matrix is shown. Because the diagonal elements are all ones, the off-diagonal elements are correlations among factors. The correlations range from  –
–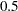 . These factors are moderately correlated.
. These factors are moderately correlated.
Output 26.19.8
Estimation of the Correlations of Factors
|
| 0.3272 |
| 0.1311 |
| 2.4955 |
| [_Parm10] |
|
| 0.4810 |
| 0.1208 |
| 3.9813 |
| [_Parm11] |
|
| 0.3272 |
| 0.1311 |
| 2.4955 |
| [_Parm10] |
|
|
| 0.3992 |
| 0.1313 |
| 3.0417 |
| [_Parm12] |
|
| 0.4810 |
| 0.1208 |
| 3.9813 |
| [_Parm11] |
|
| 0.3992 |
| 0.1313 |
| 3.0417 |
| [_Parm12] |
|
|
In Output 26.19.9, the error variances for variables are shown.
Output 26.19.9
Estimation of the Error Variances
| _Add1 |
37.24939 |
8.33997 |
4.46637 |
| _Add2 |
46.49695 |
10.69869 |
4.34604 |
| _Add3 |
15.90447 |
9.26097 |
1.71737 |
| _Add4 |
25.22889 |
7.72269 |
3.26685 |
| _Add5 |
24.89032 |
8.98327 |
2.77074 |
| _Add6 |
42.12110 |
9.20362 |
4.57658 |
| _Add7 |
27.24965 |
10.36489 |
2.62903 |
| _Add8 |
49.28881 |
11.39812 |
4.32429 |
| _Add9 |
48.10684 |
11.48868 |
4.18733 |
All  values except the one for reading3 are greater than
values except the one for reading3 are greater than 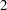 , a value close to a critical
, a value close to a critical  value at
value at 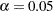 . This means that the error variance for reading3 could have been zero in the population, or it could have been nonzero but the current sample just has this insignificant value by chance (that is, a Type 2 error). Further research is needed to confirm either way.
. This means that the error variance for reading3 could have been zero in the population, or it could have been nonzero but the current sample just has this insignificant value by chance (that is, a Type 2 error). Further research is needed to confirm either way.
In addition to the parameter estimation results, PROC CALIS also outputs supplementary results that could be useful for interpretations. In Output 26.19.10, the squared multiple correlations and the factor scores regression coefficients are shown.
Output 26.19.10
Supplementary Estimation Results
| 37.24939 |
83.02400 |
0.5513 |
| 46.49695 |
108.24300 |
0.5704 |
| 15.90447 |
99.34100 |
0.8399 |
| 25.22889 |
82.21400 |
0.6931 |
| 24.89032 |
96.12500 |
0.7411 |
| 42.12110 |
88.62500 |
0.5247 |
| 27.24965 |
90.73400 |
0.6997 |
| 49.28881 |
96.54300 |
0.4895 |
| 48.10684 |
98.44500 |
0.5113 |
| 0.0200 |
0.000681 |
0.001985 |
| 0.0186 |
0.000633 |
0.001847 |
| 0.0633 |
0.002152 |
0.006275 |
| 0.001121 |
0.0403 |
0.002808 |
| 0.001271 |
0.0457 |
0.003183 |
| 0.000607 |
0.0218 |
0.001520 |
| 0.003195 |
0.002744 |
0.0513 |
| 0.001524 |
0.001309 |
0.0245 |
| 0.001611 |
0.001384 |
0.0259 |
The percentages of variance for the observed variables that can be explained by the factors are shown in the R-Square column of the table for squared multiple correlations (R-squares). These R-squares can be interpreted meaningfully because there is no reciprocal relationships among variables or correlated errors in the model. All estimates of R-squares are bounded between 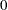 and
and  .
.
In the table for factor scores regression coefficients, entries are coefficients for the variables you can use to create the factor scores. The larger the coefficient, the more influence of the corresponding variable for creating the factor scores. It makes intuitive sense to see the cluster pattern of these coefficients—the reading measures are more important to create the latent variable scores of Read_Factor and so on.


 Classes of Statements in PROC CALIS Single-Group Analysis Syntax Multiple-Group Multiple-Model Analysis Syntax PROC CALIS Statement BOUNDS Statement BY Statement COSAN Statement COV Statement DETERM Statement EFFPART Statement FACTOR Statement FITINDEX Statement FREQ Statement GROUP Statement LINCON Statement LINEQS Statement LISMOD Statement LMTESTS Statement MATRIX Statement MEAN Statement MODEL Statement MSTRUCT Statement NLINCON Statement NLOPTIONS Statement OUTFILES Statement PARAMETERS Statement PARTIAL Statement PATH Statement PCOV Statement PVAR Statement RAM Statement REFMODEL Statement RENAMEPARM Statement SAS Programming Statements SIMTESTS Statement STD Statement STRUCTEQ Statement TESTFUNC Statement VAR Statement VARIANCE Statement VARNAMES Statement WEIGHT Statement
Classes of Statements in PROC CALIS Single-Group Analysis Syntax Multiple-Group Multiple-Model Analysis Syntax PROC CALIS Statement BOUNDS Statement BY Statement COSAN Statement COV Statement DETERM Statement EFFPART Statement FACTOR Statement FITINDEX Statement FREQ Statement GROUP Statement LINCON Statement LINEQS Statement LISMOD Statement LMTESTS Statement MATRIX Statement MEAN Statement MODEL Statement MSTRUCT Statement NLINCON Statement NLOPTIONS Statement OUTFILES Statement PARAMETERS Statement PARTIAL Statement PATH Statement PCOV Statement PVAR Statement RAM Statement REFMODEL Statement RENAMEPARM Statement SAS Programming Statements SIMTESTS Statement STD Statement STRUCTEQ Statement TESTFUNC Statement VAR Statement VARIANCE Statement VARNAMES Statement WEIGHT Statement Input Data Sets Output Data Sets The COSAN Model The FACTOR Model The LINEQS Model The LISMOD Model and Submodels The MSTRUCT Model The PATH Model The RAM Model Naming Variables and Parameters Setting Constraints on Parameters Automatic Variable Selection Estimation Criteria Relationships among Estimation Criteria Gradient, Hessian, Information Matrix, and Approximate Standard Errors Counting the Degrees of Freedom Assessment of Fit Total, Direct, and Indirect Effects Standardized Solutions Modification Indices Missing Values and the Analysis of Missing Patterns Measures of Multivariate Kurtosis Initial Estimates Use of Optimization Techniques Computational Problems Displayed Output ODS Table Names ODS Graphics
Input Data Sets Output Data Sets The COSAN Model The FACTOR Model The LINEQS Model The LISMOD Model and Submodels The MSTRUCT Model The PATH Model The RAM Model Naming Variables and Parameters Setting Constraints on Parameters Automatic Variable Selection Estimation Criteria Relationships among Estimation Criteria Gradient, Hessian, Information Matrix, and Approximate Standard Errors Counting the Degrees of Freedom Assessment of Fit Total, Direct, and Indirect Effects Standardized Solutions Modification Indices Missing Values and the Analysis of Missing Patterns Measures of Multivariate Kurtosis Initial Estimates Use of Optimization Techniques Computational Problems Displayed Output ODS Table Names ODS Graphics Estimating Covariances and Correlations Estimating Covariances and Means Simultaneously Testing Uncorrelatedness of Variables Testing Covariance Patterns Testing Some Standard Covariance Pattern Hypotheses Linear Regression Model Multivariate Regression Models Measurement Error Models Testing Specific Measurement Error Models Measurement Error Models with Multiple Predictors Measurement Error Models Specified As Linear Equations Confirmatory Factor Models Confirmatory Factor Models: Some Variations The Full Information Maximum Likelihood Method Comparing the ML and FIML Estimation Path Analysis: Stability of Alienation Simultaneous Equations with Mean Structures and Reciprocal Paths Fitting Direct Covariance Structures Confirmatory Factor Analysis: Cognitive Abilities Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis Testing Equality of Covariance and Mean Matrices between Independent Groups Illustrating Various General Modeling Languages Testing Competing Path Models for the Career Aspiration Data Fitting a Latent Growth Curve Model Higher-Order and Hierarchical Factor Models Linear Relations among Factor Loadings Multiple-Group Model for Purchasing Behavior Fitting the RAM and EQS Models by the COSAN Modeling Language Second-Order Confirmatory Factor Analysis Linear Relations among Factor Loadings: COSAN Model Specification Ordinal Relations among Factor Loadings Longitudinal Factor Analysis
Estimating Covariances and Correlations Estimating Covariances and Means Simultaneously Testing Uncorrelatedness of Variables Testing Covariance Patterns Testing Some Standard Covariance Pattern Hypotheses Linear Regression Model Multivariate Regression Models Measurement Error Models Testing Specific Measurement Error Models Measurement Error Models with Multiple Predictors Measurement Error Models Specified As Linear Equations Confirmatory Factor Models Confirmatory Factor Models: Some Variations The Full Information Maximum Likelihood Method Comparing the ML and FIML Estimation Path Analysis: Stability of Alienation Simultaneous Equations with Mean Structures and Reciprocal Paths Fitting Direct Covariance Structures Confirmatory Factor Analysis: Cognitive Abilities Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis Testing Equality of Covariance and Mean Matrices between Independent Groups Illustrating Various General Modeling Languages Testing Competing Path Models for the Career Aspiration Data Fitting a Latent Growth Curve Model Higher-Order and Hierarchical Factor Models Linear Relations among Factor Loadings Multiple-Group Model for Purchasing Behavior Fitting the RAM and EQS Models by the COSAN Modeling Language Second-Order Confirmatory Factor Analysis Linear Relations among Factor Loadings: COSAN Model Specification Ordinal Relations among Factor Loadings Longitudinal Factor Analysis does not change much from the initial function value
does not change much from the initial function value  , as shown in Output 26.19.3.
, as shown in Output 26.19.3. 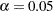 . The RMSEA estimate is
. The RMSEA estimate is 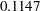 , which is not indicative of a good fit according to Browne and Cudeck (1993) Other indices might suggest only a marginal good fit. For example, Bentler’s comparative fit index and Bollen nonnormed index delta2 are both above 0.90. However, many other do not attain this 0.90 level. For example, adjusted GFI is only
, which is not indicative of a good fit according to Browne and Cudeck (1993) Other indices might suggest only a marginal good fit. For example, Bentler’s comparative fit index and Bollen nonnormed index delta2 are both above 0.90. However, many other do not attain this 0.90 level. For example, adjusted GFI is only 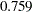 . It is thus safe to conclude that there could be some improvements on the model fit.
. It is thus safe to conclude that there could be some improvements on the model fit.  . This is an approximation of the chi-square drop if this parameter was included in the model. The Pr > ChiSq value of
. This is an approximation of the chi-square drop if this parameter was included in the model. The Pr > ChiSq value of  indicates a significant improvement of model fit at
indicates a significant improvement of model fit at 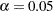 . Nine more new loading parameters are suggested in the table, with less and less statistical significance in the change of model fit chi-square. Note that these approximate chi-squares are one-at-a-time chi-square changes. That means that the overall chi-square drop is not a simple sum of individual chi-square changes when you include two or more new parameters in the modified model.
. Nine more new loading parameters are suggested in the table, with less and less statistical significance in the change of model fit chi-square. Note that these approximate chi-squares are one-at-a-time chi-square changes. That means that the overall chi-square drop is not a simple sum of individual chi-square changes when you include two or more new parameters in the modified model.  , which is smaller than that of the largest LM Stat for the factor loading parameters. Despite this, it is more reasonable to add the covariance parameters among factors first to determine whether that improves the model fit.
, which is smaller than that of the largest LM Stat for the factor loading parameters. Despite this, it is more reasonable to add the covariance parameters among factors first to determine whether that improves the model fit. 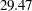 , which is about
, which is about  less than the model with uncorrelated factors. The
less than the model with uncorrelated factors. The 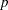 -value is
-value is  , indicating a satisfactory model fit. The RMSEA value is
, indicating a satisfactory model fit. The RMSEA value is  , which is close to
, which is close to  , a value recommended as an indication of good model fit by Browne and Cudeck (1993) More fit indices that do not attain the
, a value recommended as an indication of good model fit by Browne and Cudeck (1993) More fit indices that do not attain the  level with the uncorrelated factor model now have values close to or above
level with the uncorrelated factor model now have values close to or above  . These include the goodness-of-fit index (GFI), McDonald centrality, Bentler-Bonnet NFI, and Bentler-Bonnet nonnormed index. By all counts, the correlated factor model is a much better fit than the uncorrelated factor model.
. These include the goodness-of-fit index (GFI), McDonald centrality, Bentler-Bonnet NFI, and Bentler-Bonnet nonnormed index. By all counts, the correlated factor model is a much better fit than the uncorrelated factor model.  –
–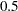 . These factors are moderately correlated.
. These factors are moderately correlated.  values except the one for reading3 are greater than
values except the one for reading3 are greater than 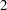 , a value close to a critical
, a value close to a critical  value at
value at 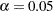 . This means that the error variance for reading3 could have been zero in the population, or it could have been nonzero but the current sample just has this insignificant value by chance (that is, a Type 2 error). Further research is needed to confirm either way.
. This means that the error variance for reading3 could have been zero in the population, or it could have been nonzero but the current sample just has this insignificant value by chance (that is, a Type 2 error). Further research is needed to confirm either way. 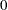 and
and  .
.