The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingSeasonal Dummies and Time TrendsBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelVector Error Correction Model in ARMA FormMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
Tentative Order Selection
Sample Cross-Covariance and Cross-Correlation Matrices
Given a stationary multivariate time series 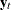 , cross-covariance matrices are
, cross-covariance matrices are
![\[ \Gamma (l)=\mr{E} [(\mb{y} _ t - \bmu )(\mb{y} _{t+l} -\bmu )’] \]](images/etsug_varmax0478.png)
where 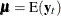 , and cross-correlation matrices are
, and cross-correlation matrices are
![\[ \rho (l) = D^{-1}\Gamma (l)D^{-1} \]](images/etsug_varmax0480.png)
where D is a diagonal matrix with the standard deviations of the components of 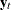 on the diagonal.
on the diagonal.
The sample cross-covariance matrix at lag l, denoted as 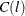 , is computed as
, is computed as
![\[ \hat\Gamma (l) = C(l) =\frac{1}{T} \sum _{t=1}^{T-l}{{\tilde{\mb{y}} }_{t}{\tilde{\mb{y}} }’_{t+l}} \]](images/etsug_varmax0482.png)
where 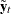 is the centered data and
is the centered data and 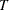 is the number of nonmissing observations. Thus, the (i, j) element of
is the number of nonmissing observations. Thus, the (i, j) element of 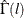 is
is 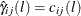 . The sample cross-correlation matrix at lag l is computed as
. The sample cross-correlation matrix at lag l is computed as
![\[ \hat\rho _{ij}(l) = c_{ij}(l) /[c_{ii}(0)c_{jj}(0)]^{1/2}, ~ ~ i,j=1,\ldots , k \]](images/etsug_varmax0487.png)
The following statements use the CORRY option to compute the sample cross-correlation matrices and their summary indicator
plots in terms of 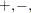 and
and  , where + indicates significant positive cross-correlations,
, where + indicates significant positive cross-correlations,  indicates significant negative cross-correlations, and
indicates significant negative cross-correlations, and  indicates insignificant cross-correlations.
indicates insignificant cross-correlations.
proc varmax data=simul1;
model y1 y2 / p=1 noint lagmax=3 print=(corry)
printform=univariate;
run;
Figure 42.54 shows the sample cross-correlation matrices of 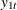 and
and 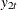 . As shown, the sample autocorrelation functions for each variable decay quickly, but are significant with respect to two
standard errors.
. As shown, the sample autocorrelation functions for each variable decay quickly, but are significant with respect to two
standard errors.
Figure 42.54: Cross-Correlations (CORRY Option)
| Cross Correlations of Dependent Series by Variable |
|||
|---|---|---|---|
| Variable | Lag | y1 | y2 |
| y1 | 0 | 1.00000 | 0.67041 |
| 1 | 0.83143 | 0.84330 | |
| 2 | 0.56094 | 0.81972 | |
| 3 | 0.26629 | 0.66154 | |
| y2 | 0 | 0.67041 | 1.00000 |
| 1 | 0.29707 | 0.77132 | |
| 2 | -0.00936 | 0.48658 | |
| 3 | -0.22058 | 0.22014 | |
| Schematic Representation of Cross Correlations |
||||
|---|---|---|---|---|
| Variable/Lag | 0 | 1 | 2 | 3 |
| y1 | ++ | ++ | ++ | ++ |
| y2 | ++ | ++ | .+ | -+ |
| + is > 2*std error, - is < -2*std error, . is between | ||||
Partial Autoregressive Matrices
For each 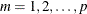 you can define a sequence of matrices
you can define a sequence of matrices 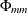 , which is called the partial autoregression matrices of lag m, as the solution for
, which is called the partial autoregression matrices of lag m, as the solution for 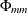 to the Yule-Walker equations of order m,
to the Yule-Walker equations of order m,
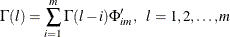
The sequence of the partial autoregression matrices 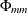 of order m has the characteristic property that if the process follows the AR(p), then
of order m has the characteristic property that if the process follows the AR(p), then 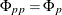 and
and 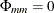 for
for 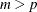 . Hence, the matrices
. Hence, the matrices 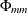 have the cutoff property for a VAR(p) model, and so they can be useful in the identification of the order of a pure VAR model.
have the cutoff property for a VAR(p) model, and so they can be useful in the identification of the order of a pure VAR model.
The following statements use the PARCOEF option to compute the partial autoregression matrices:
proc varmax data=simul1;
model y1 y2 / p=1 noint lagmax=3
printform=univariate
print=(corry parcoef pcorr
pcancorr roots);
run;
Figure 42.55 shows that the model can be obtained by an AR order 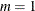 since partial autoregression matrices are insignificant after lag 1 with respect to two standard errors. The matrix for lag
1 is the same as the Yule-Walker autoregressive matrix.
since partial autoregression matrices are insignificant after lag 1 with respect to two standard errors. The matrix for lag
1 is the same as the Yule-Walker autoregressive matrix.
Figure 42.55: Partial Autoregression Matrices (PARCOEF Option)
| Partial Autoregression | |||
|---|---|---|---|
| Lag | Variable | y1 | y2 |
| 1 | y1 | 1.14844 | -0.50954 |
| y2 | 0.54985 | 0.37409 | |
| 2 | y1 | -0.00724 | 0.05138 |
| y2 | 0.02409 | 0.05909 | |
| 3 | y1 | -0.02578 | 0.03885 |
| y2 | -0.03720 | 0.10149 | |
| Schematic Representation of Partial Autoregression |
|||
|---|---|---|---|
| Variable/Lag | 1 | 2 | 3 |
| y1 | +- | .. | .. |
| y2 | ++ | .. | .. |
| + is > 2*std error, - is < -2*std error, . is between | |||
Partial Correlation Matrices
Define the forward autoregression
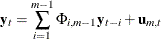
and the backward autoregression
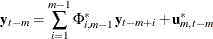
The matrices 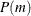 defined by Ansley and Newbold (1979) are given by
defined by Ansley and Newbold (1979) are given by
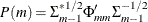
where
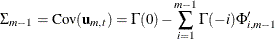
and
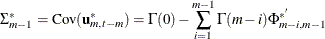
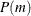 are the partial cross-correlation matrices at lag m between the elements of
are the partial cross-correlation matrices at lag m between the elements of 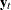 and
and 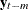 , given
, given 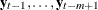 . The matrices
. The matrices 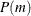 have the cutoff property for a VAR(p) model, and so they can be useful in the identification of the order of a pure VAR structure.
have the cutoff property for a VAR(p) model, and so they can be useful in the identification of the order of a pure VAR structure.
The following statements use the PCORR option to compute the partial cross-correlation matrices:
proc varmax data=simul1;
model y1 y2 / p=1 noint lagmax=3
print=(pcorr)
printform=univariate;
run;
The partial cross-correlation matrices in Figure 42.56 are insignificant after lag 1 with respect to two standard errors. This indicates that an AR order of 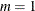 can be an appropriate choice.
can be an appropriate choice.
Figure 42.56: Partial Correlations (PCORR Option)
| Partial Cross Correlations by Variable | |||
|---|---|---|---|
| Variable | Lag | y1 | y2 |
| y1 | 1 | 0.80348 | 0.42672 |
| 2 | 0.00276 | 0.03978 | |
| 3 | -0.01091 | 0.00032 | |
| y2 | 1 | -0.30946 | 0.71906 |
| 2 | 0.04676 | 0.07045 | |
| 3 | 0.01993 | 0.10676 | |
| Schematic Representation of Partial Cross Correlations |
|||
|---|---|---|---|
| Variable/Lag | 1 | 2 | 3 |
| y1 | ++ | .. | .. |
| y2 | -+ | .. | .. |
| + is > 2*std error, - is < -2*std error, . is between | |||
Partial Canonical Correlation Matrices
The partial canonical correlations at lag m between the vectors 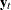 and
and 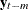 , given
, given 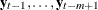 , are
, are 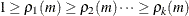 . The partial canonical correlations are the canonical correlations between the residual series
. The partial canonical correlations are the canonical correlations between the residual series 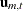 and
and 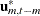 , where
, where 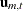 and
and 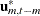 are defined in the previous section. Thus, the squared partial canonical correlations
are defined in the previous section. Thus, the squared partial canonical correlations 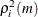 are the eigenvalues of the matrix
are the eigenvalues of the matrix
![\[ \{ \mr{Cov} (\mb{u} _{m,t})\} ^{-1} \mr{E} (\mb{u} _{m,t} \mb{u} _{m,t-m}^{*'}) \{ \mr{Cov} (\mb{u} _{m,t-m}^{*})\} ^{-1} \mr{E} (\mb{u} _{m,t-m}^{*} \mb{u} _{m,t}^{'}) = \Phi _{mm}^{*'} \Phi _{mm}^{'} \]](images/etsug_varmax0506.png)
It follows that the test statistic to test for 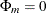 in the VAR model of order
in the VAR model of order 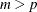 is approximately
is approximately
![\[ (T-m)\mr{~ tr~ } \{ \Phi _{mm}^{*'} \Phi _{mm}^{'} \} \approx (T-m)\sum _{i=1}^ k \rho _ i^2(m) \]](images/etsug_varmax0508.png)
and has an asymptotic chi-square distribution with 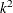 degrees of freedom for
degrees of freedom for 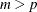 .
.
The following statements use the PCANCORR option to compute the partial canonical correlations:
proc varmax data=simul1; model y1 y2 / p=1 noint lagmax=3 print=(pcancorr); run;
Figure 42.57 shows that the partial canonical correlations 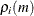 between
between 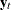 and
and 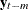 are {0.918, 0.773}, {0.092, 0.018}, and {0.109, 0.011} for lags
are {0.918, 0.773}, {0.092, 0.018}, and {0.109, 0.011} for lags 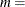 1 to 3. After lag
1 to 3. After lag 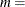 1, the partial canonical correlations are insignificant with respect to the 0.05 significance level, indicating that an AR
order of
1, the partial canonical correlations are insignificant with respect to the 0.05 significance level, indicating that an AR
order of 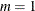 can be an appropriate choice.
can be an appropriate choice.
Figure 42.57: Partial Canonical Correlations (PCANCORR Option)
The Minimum Information Criterion (MINIC) Method
The minimum information criterion (MINIC) method can tentatively identify the orders of a VARMA(p,q) process (Spliid 1983; Koreisha and Pukkila 1989; Quinn 1980). The first step of this method is to obtain estimates of the innovations series, 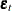 , from the VAR(
, from the VAR(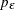 ), where
), where 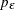 is chosen sufficiently large. The choice of the autoregressive order,
is chosen sufficiently large. The choice of the autoregressive order, 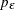 , is determined by use of a selection criterion. From the selected VAR(
, is determined by use of a selection criterion. From the selected VAR(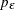 ) model, you obtain estimates of residual series
) model, you obtain estimates of residual series
![\[ \tilde{ \bepsilon _ t} = \mb{y} _ t - \sum _{i=1}^{p_{\epsilon }} {\hat\Phi }_{i}^{p_{\epsilon }} \mb{y} _{t-i} - {\hat{\bdelta }}^{p_{\epsilon }}, ~ ~ t=p_{\epsilon }+1, \ldots , T \]](images/etsug_varmax0513.png)
In the second step, you select the order (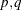 ) of the VARMA model for p in
) of the VARMA model for p in 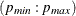 and q in
and q in 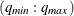
![\[ \mb{y} _ t = \bdelta + \sum _{i=1}^{p}{\Phi _{i}}\mb{y} _{t-i} - \sum _{i=1}^{q}{\Theta _{i}} \tilde{\bepsilon }_{t-i} + {\bepsilon _ t} \]](images/etsug_varmax0517.png)
which minimizes a selection criterion like SBC or HQ.
According to Lütkepohl (1993), the information criteria, namely Akaike’s information criterion (AIC), the corrected Akaike’s information criterion (AICC), the final prediction error criterion (FPE), the Hannan-Quinn criterion (HQC), and the Schwarz Bayesian criterion (SBC), are defined as
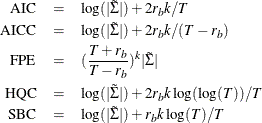
where 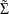 is the maximum likelihood estimate of the innovation covariance matrix
is the maximum likelihood estimate of the innovation covariance matrix 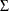 ,
, 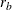 is the number of parameters in each mean equation, k is the number of dependent variables, and T is the number of observations used to estimate the model. Compared to the definitions of AIC, AICC, HQC, and SBC discussed
in the section Multivariate Model Diagnostic Checks, the preceding definitions omit some constant terms and are normalized by T. More specifically, only the parameters in each of the mean equations are counted; the parameters in the innovation covariance
matrix
is the number of parameters in each mean equation, k is the number of dependent variables, and T is the number of observations used to estimate the model. Compared to the definitions of AIC, AICC, HQC, and SBC discussed
in the section Multivariate Model Diagnostic Checks, the preceding definitions omit some constant terms and are normalized by T. More specifically, only the parameters in each of the mean equations are counted; the parameters in the innovation covariance
matrix  are not counted.
are not counted.
The following statements use the MINIC= option to compute a table that contains the information criterion associated with various AR and MA orders:
proc varmax data=simul1; model y1 y2 / p=1 noint minic=(p=3 q=3); run;
Figure 42.58 shows the output associated with the MINIC= option. The criterion takes the smallest value at AR order 1.
Figure 42.58: MINIC= Option