The VARMAX Procedure

Dynamic Simultaneous Equations Modeling

In the econometrics literature, the VARMAX(p,q,s) model is sometimes written in a form that is slightly different than the one shown in the previous section. This alternative form is referred to as a dynamic simultaneous equations model or a dynamic structural equations model.

Because 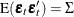$\mr{E} (\bepsilon _ t \bepsilon _ t’)=\Sigma $ is assumed to be positive-definite, there exists a lower triangular matrix 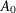$A_0$ that has ones on the diagonals such that 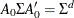$A_0\Sigma A_0’=\Sigma ^ d$, where 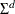$\Sigma ^ d$ is a diagonal matrix that has positive diagonal elements.

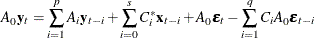
\begin{eqnarray*} A_0 \mb{y} _ t = \sum _{i=1}^{p} A_ i\mb{y} _{t-i} + \sum _{i=0}^{s}C_ i^*\mb{x} _{t-i} + A_0\bepsilon _ t - \sum _{i=1}^{q}C_ i A_0 \bepsilon _{t-i} \end{eqnarray*}

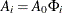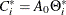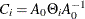where $A_ i = A_0 \Phi _ i$, $C_ i^* = A_0 \Theta _ i^*$, and $C_ i = A_0 \Theta _ i A_0^{-1} $.

As an alternative form,

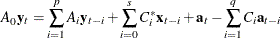
\begin{eqnarray*} A_0 \mb{y} _ t = \sum _{i=1}^{p} A_ i\mb{y} _{t-i} + \sum _{i=0}^{s}C_ i^*\mb{x} _{t-i} + \mb{a}_ t - \sum _{i=1}^{q}C_ i\mb{a}_{t-i} \end{eqnarray*}

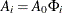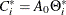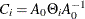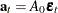where $A_ i = A_0 \Phi _ i$, $C_ i^* = A_0 \Theta _ i^*$, $C_ i = A_0 \Theta _ i A_0^{-1} $, and $\mb{a}_ t = A_0\bepsilon _ t$. The covariance matrix of 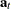$\mb{a}_ t$ is the diagonal matrix 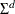$\Sigma ^ d$. The PRINT=(DYNAMIC) option returns the parameter estimates that result from estimating the model in this form.

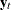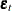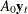A dynamic simultaneous equations model involves a leading (lower triangular) coefficient matrix for $\mb{y} _ t$ at lag 0 or a leading coefficient matrix for $\bepsilon _ t$ at lag 0. Such a representation of the VARMAX(p,q,s) model can be more useful in certain circumstances than the standard representation. From the linear combination of the dependent variables obtained by $A_0 \mb{y} _ t$, you can easily see the relationship between the dependent variables in the current time.

The following statements provide the dynamic simultaneous equations of the VAR(1) model. 

proc iml;
   sig = {1.0  0.5, 0.5 1.25};
   phi = {1.2 -0.5, 0.6 0.3};
   /* simulate the vector time series */
   call varmasim(y,phi) sigma = sig n = 100 seed = 34657;
   cn = {'y1' 'y2'};
   create simul1 from y[colname=cn];
   append from y;
quit;

data simul1;
   set simul1;
   date = intnx( 'year', '01jan1900'd, _n_-1 );
   format date year4.;
run;

proc varmax data=simul1;
   model y1 y2 / p=1 noint print=(dynamic);
run;

This is the same data set and model used in the section Getting Started: VARMAX Procedure. You can compare the results of the VARMA model form and the dynamic simultaneous equations model form.

Figure 42.40: Dynamic Simultaneous Equations (DYNAMIC Option)

The VARMAX Procedure

Covariances of Innovations
Variable y1 y2
y1 1.28875 0.00000
y2 0.00000 1.29578

AR
Lag Variable y1 y2
0 y1 1.00000 0.00000
  y2 -0.30845 1.00000
1 y1 1.15977 -0.51058
  y2 0.18861 0.54247

Dynamic Model Parameter Estimates
Equation Parameter Estimate Standard
Error 		t Value Pr > |t| Variable
y1 AR1_1_1 1.15977 0.05508 21.06 0.0001 y1(t-1)
  AR1_1_2 -0.51058 0.07140 -7.15 0.0001 y2(t-1)
y2 AR0_2_1 0.30845       y1(t)
  AR1_2_1 0.18861 0.05779 3.26 0.0015 y1(t-1)
  AR1_2_2 0.54247 0.07491 7.24 0.0001 y2(t-1) 




            

            


            
In Figure 42.4 in the section Getting Started: VARMAX Procedure, the covariance of 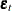$\bepsilon _ t$ estimated from the VARMAX model form is 
            

            

               
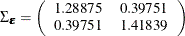
\begin{eqnarray*} \Sigma _{\bepsilon } = \left( \begin{array}{rr} 1.28875 & 0.39751 \\ 0.39751 & 1.41839 \end{array} \right) \end{eqnarray*}

            

            
 Figure 42.40 shows the results from estimating the model as a dynamic simultaneous equations model. By the decomposition of 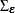$\Sigma _{\bepsilon }$, you get a diagonal matrix (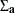$\Sigma _\mb {{a}} $) and a lower triangular matrix (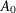$A_0$) such as 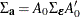$\Sigma _\mb {{a}} = A_0 \Sigma _{\bepsilon } A_0’$ where 
            

            

               
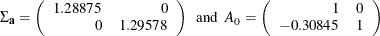
\begin{eqnarray*} \Sigma _\mb {{a}} = \left( \begin{array}{rr} 1.28875 & 0 \\ 0 & 1.29578 \end{array} \right) ~ ~ \mr{and} ~ ~ A_0 =\left( \begin{array}{rr} 1 & 0 \\ -0.30845 & 1 \end{array} \right) \end{eqnarray*}

            

            
 The lower triangular matrix (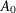$A_0$) is shown in the left side of the simultaneous equations model. The parameter estimates in equations system are shown in
               the right side of the two-equations system. 
            

            
The simultaneous equations model is written as 

            

               
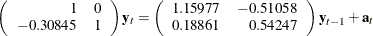
\begin{eqnarray*} \left( \begin{array}{rr} 1 & 0 \\ -0.30845 & 1 \end{array} \right) \mb{y} _ t = \left( \begin{array}{rr} 1.15977 & -0.51058 \\ 0.18861 & 0.54247 \end{array} \right) \mb{y} _{t-1} + \mb{a}_ t \end{eqnarray*}

            

            
 The resulting two-equation system can be written as 

            

               
\begin{eqnarray*} y_{1t} & =& 1.15977 y_{1,t-1} - 0.51058 y_{2,t-1} + a_{1t} \\ y_{2t} & =& 0.30845 y_{1t} + 0.18861 y_{1,t-1} + 0.54247 y_{2,t-1} + a_{2t} \\ \end{eqnarray*}