The PROBIT Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PROBIT StatementBY StatementCDFPLOT StatementCLASS StatementEFFECTPLOT StatementESTIMATE StatementINSET StatementIPPPLOT StatementLPREDPLOT StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementPREDPPLOT StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PROBIT StatementBY StatementCDFPLOT StatementCLASS StatementEFFECTPLOT StatementESTIMATE StatementINSET StatementIPPPLOT StatementLPREDPLOT StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementPREDPPLOT StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingComputational MethodDistributionsINEST= SAS-data-setModel SpecificationLack-of-Fit TestsRescaling the Covariance MatrixTolerance DistributionInverse Confidence LimitsOUTEST= SAS-data-setXDATA= SAS-data-setTraditional High-Resolution GraphicsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingComputational MethodDistributionsINEST= SAS-data-setModel SpecificationLack-of-Fit TestsRescaling the Covariance MatrixTolerance DistributionInverse Confidence LimitsOUTEST= SAS-data-setXDATA= SAS-data-setTraditional High-Resolution GraphicsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Example 93.4 An Epidemiology Study
The data in this example, which are from an epidemiology study, consist of five variables: the number, r, of individuals surviving after an epidemic, out of n treated, for combinations of medicine dosage (dose), treatment (treat = A, B), and sex (sex = 0(Female), 1(Male)).
To see whether the two treatments have different effects on male and female individual survival rates, the interaction term
between the two variables treat and sex is included in the model.
The following invocation of PROC PROBIT fits the binary probit model to the grouped data:
data epidemic; input treat$ dose n r sex @@; label dose = Dose; datalines; A 2.17 142 142 0 A .57 132 47 1 A 1.68 128 105 1 A 1.08 126 100 0 A 1.79 125 118 0 B 1.66 117 115 1 B 1.49 127 114 0 B 1.17 51 44 1 B 2.00 127 126 0 B .80 129 100 1 ; data xval; input treat $ dose sex; datalines; B 2. 1 ;
proc probit optc lackfit covout data=epidemic
outest = out1 xdata = xval
Plots=(predpplot ippplot lpredplot);
class treat sex;
model r/n = dose treat sex sex*treat/corrb covb inversecl;
output out = out2 p =p;
run;
The results of this analysis are shown in the outputs that follow.
Output 93.4.1 displays the table of level information for all classification variables in the CLASS statement.
Output 93.4.1: Class Level Information
Output 93.4.2 displays the table of parameter information for the effects in the MODEL statement.
Output 93.4.2: Parameter Information
Output 93.4.3 displays background information about the model fit. Included are the name of the input data set, the response variables used, the numbers of observations, events, and trials, the type of distribution, and the final value of the log-likelihood function.
Output 93.4.3: Model Information
Output 93.4.4 displays the table of goodness-of-fit tests requested with the LACKFIT option in the PROC PROBIT statement. Two goodness-of-fit statistics, the Pearson’s chi-square statistic and the likelihood ratio chi-square statistic, are computed. The grouping method for computing these statistics can be specified by the AGGREGATE= option. The details can be found in the AGGREGATE= option, and an example can be found in the second part of this example. By default, the PROBIT procedure uses the covariates in the MODEL statement to do grouping. Observations with the same values of the covariates in the MODEL statement are grouped into cells and the two statistics are computed according to these cells. The total number of cells and the number of levels for the response variable are reported next in the "Response-Covariate Profile."
In this example, neither the Pearson’s chi-square nor the log-likelihood ratio chi-square tests are significant at the 0.1
level, which is the default test level used by the PROBIT procedure. That means that the model, which includes the interaction
of treat and sex, is suitable for this epidemiology data set. (Further investigation shows that models without the interaction of treat and sex are not acceptable by either test.)
Output 93.4.4: Goodness-of-Fit Tests and Response-Covariate Profile
Output 93.4.5 displays the Type III test results for all effects specified in the MODEL statement, which include the degrees of freedom for the effect, the Wald Chi-Square test statistic, and the p-value.
Output 93.4.5: Type III Tests
Output 93.4.6 displays the table of parameter estimates for the model. The PROBIT procedure displays information for all the parameters of an effect. Degenerate parameters are indicated by 0 degree of freedom. Confidence intervals are computed for all parameters with nonzero degrees of freedom, including the natural threshold C if the OPTC option is specified in the PROC PROBIT statement. The confidence level can be specified by the ALPHA= option in the MODEL statement. The default confidence level is 95%.
Output 93.4.6: Analysis of Parameter Estimates
| Analysis of Maximum Likelihood Parameter Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
95% Confidence Limits | Chi-Square | Pr > ChiSq | |||
| Intercept | 1 | -0.8871 | 0.3632 | -1.5991 | -0.1752 | 5.96 | 0.0146 | ||
| dose | 1 | 1.6774 | 0.2583 | 1.1711 | 2.1837 | 42.17 | <.0001 | ||
| treat | A | 1 | -1.2537 | 0.2616 | -1.7664 | -0.7410 | 22.97 | <.0001 | |
| treat | B | 0 | 0.0000 | . | . | . | . | . | |
| sex | 0 | 1 | -0.4633 | 0.2289 | -0.9119 | -0.0147 | 4.10 | 0.0429 | |
| sex | 1 | 0 | 0.0000 | . | . | . | . | . | |
| treat*sex | A | 0 | 1 | 1.2899 | 0.3456 | 0.6126 | 1.9672 | 13.93 | 0.0002 |
| treat*sex | A | 1 | 0 | 0.0000 | . | . | . | . | . |
| treat*sex | B | 0 | 0 | 0.0000 | . | . | . | . | . |
| treat*sex | B | 1 | 0 | 0.0000 | . | . | . | . | . |
| _C_ | 1 | 0.2735 | 0.0946 | 0.0881 | 0.4589 | ||||
From Output 93.4.6, you can see the following results:
-
The variable
dosehas a significant positive effect on the survival rate. -
Individuals under treatment A have a lower survival rate.
-
Male individuals have a higher survival rate.
-
Female individuals under treatment A have a higher survival rate.
Output 93.4.7 and Output 93.4.8 display tables of estimated covariance matrix and estimated correlation matrix for estimated parameters with a nonzero degree of freedom, respectively. They are computed by the inverse of the Hessian matrix of the estimated parameters.
Output 93.4.7: Estimated Covariance Matrix
| Estimated Covariance Matrix | ||||||
|---|---|---|---|---|---|---|
| Intercept | dose | treatA | sex0 | treatAsex0 | _C_ | |
| Intercept | 0.131944 | -0.087353 | 0.053551 | 0.030285 | -0.067056 | -0.028073 |
| dose | -0.087353 | 0.066723 | -0.047506 | -0.034081 | 0.058620 | 0.018196 |
| treatA | 0.053551 | -0.047506 | 0.068425 | 0.036063 | -0.075323 | -0.017084 |
| sex0 | 0.030285 | -0.034081 | 0.036063 | 0.052383 | -0.063599 | -0.008088 |
| treatAsex0 | -0.067056 | 0.058620 | -0.075323 | -0.063599 | 0.119408 | 0.019134 |
| _C_ | -0.028073 | 0.018196 | -0.017084 | -0.008088 | 0.019134 | 0.008948 |
Output 93.4.8: Estimated Correlation Matrix
| Estimated Correlation Matrix | ||||||
|---|---|---|---|---|---|---|
| Intercept | dose | treatA | sex0 | treatAsex0 | _C_ | |
| Intercept | 1.000000 | -0.930998 | 0.563595 | 0.364284 | -0.534227 | -0.817027 |
| dose | -0.930998 | 1.000000 | -0.703083 | -0.576477 | 0.656744 | 0.744699 |
| treatA | 0.563595 | -0.703083 | 1.000000 | 0.602359 | -0.833299 | -0.690420 |
| sex0 | 0.364284 | -0.576477 | 0.602359 | 1.000000 | -0.804154 | -0.373565 |
| treatAsex0 | -0.534227 | 0.656744 | -0.833299 | -0.804154 | 1.000000 | 0.585364 |
| _C_ | -0.817027 | 0.744699 | -0.690420 | -0.373565 | 0.585364 | 1.000000 |
Output 93.4.9 displays the computed values and fiducial limits for the first single continuous variable dose in the MODEL statement, given the probability levels, without the effect of the natural threshold, and when the option INSERSECL
in the MODEL statement is specified. If there is no single continuous variable in the MODEL specification but the INVERSECL
option is specified, an error is reported.
Output 93.4.9: Probit Analysis on Dose
| Probit Analysis on dose | |||
|---|---|---|---|
| Probability | dose | 95% Fiducial Limits | |
| 0.01 | -0.85801 | -1.81301 | -0.33743 |
| 0.02 | -0.69549 | -1.58167 | -0.21116 |
| 0.03 | -0.59238 | -1.43501 | -0.13093 |
| 0.04 | -0.51482 | -1.32476 | -0.07050 |
| 0.05 | -0.45172 | -1.23513 | -0.02130 |
| 0.06 | -0.39802 | -1.15888 | 0.02063 |
| 0.07 | -0.35093 | -1.09206 | 0.05742 |
| 0.08 | -0.30877 | -1.03226 | 0.09039 |
| 0.09 | -0.27043 | -0.97790 | 0.12040 |
| 0.10 | -0.23513 | -0.92788 | 0.14805 |
| 0.15 | -0.08900 | -0.72107 | 0.26278 |
| 0.20 | 0.02714 | -0.55706 | 0.35434 |
| 0.25 | 0.12678 | -0.41669 | 0.43322 |
| 0.30 | 0.21625 | -0.29095 | 0.50437 |
| 0.35 | 0.29917 | -0.17477 | 0.57064 |
| 0.40 | 0.37785 | -0.06487 | 0.63387 |
| 0.45 | 0.45397 | 0.04104 | 0.69546 |
| 0.50 | 0.52888 | 0.14481 | 0.75654 |
| 0.55 | 0.60380 | 0.24800 | 0.81819 |
| 0.60 | 0.67992 | 0.35213 | 0.88157 |
| 0.65 | 0.75860 | 0.45879 | 0.94803 |
| 0.70 | 0.84151 | 0.56985 | 1.01942 |
| 0.75 | 0.93099 | 0.68770 | 1.09847 |
| 0.80 | 1.03063 | 0.81571 | 1.18970 |
| 0.85 | 1.14677 | 0.95926 | 1.30171 |
| 0.90 | 1.29290 | 1.12867 | 1.45386 |
| 0.91 | 1.32819 | 1.16747 | 1.49273 |
| 0.92 | 1.36654 | 1.20867 | 1.53590 |
| 0.93 | 1.40870 | 1.25284 | 1.58450 |
| 0.94 | 1.45579 | 1.30084 | 1.64012 |
| 0.95 | 1.50949 | 1.35397 | 1.70515 |
| 0.96 | 1.57258 | 1.41443 | 1.78353 |
| 0.97 | 1.65015 | 1.48626 | 1.88238 |
| 0.98 | 1.75326 | 1.57833 | 2.01720 |
| 0.99 | 1.91577 | 1.71776 | 2.23537 |
If the XDATA= option is used to input a data set for the independent variables in the MODEL statement, the PROBIT procedure
uses these values for the independent variables other than the single continuous variable. Missing values are not permitted
in the XDATA= data set for the independent variables, although the value for the single continuous variable is not used in
the computing of the fiducial limits. A suitable valid value should be given. In the data set xval created by the SAS statements on , dose = 2. Only one observation from the XDATA= data set is used to produce a probit analysis table for a combination of classification
variable levels. If more than one observation is present in the XDATA= data set, only the last observation is used.
See the section XDATA= SAS-data-set for the default values for those effects other than the single continuous variable, for which the fiducial limits are computed.
In this example, there are two classification variables, treat and sex. Fiducial limits for the dose variable are computed for the highest level of the classification variables, treat = B and sex = 1, which is the default specification. Since these are the default values, you would get the same values and fiducial limits
if you did not specify the XDATA= option in this example. The confidence level for the fiducial limits can be specified by
the ALPHA= option in the MODEL statement. The default level is 95%.
If a LOG10 or LOG option is used in the PROC PROBIT statement, the values and the fiducial limits are computed for both the single continuous variable and its logarithm.
Output 93.4.10 displays the OUTEST= data set. All parameters for an effect are included. The name of a parameter is generated by combining the variable names and levels in the effect. The maximum length of a parameter name is 32.
Output 93.4.10: Outest Data Set for Epidemiology Study
| Obs | _MODEL_ | _NAME_ | _TYPE_ | _DIST_ | _STATUS_ | _LNLIKE_ | r | Intercept | dose | treatA | treatB | sex0 | sex1 | treatAsex0 | treatAsex1 | treatBsex0 | treatBsex1 | _C_ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | r | PARMS | Normal | 0 Converged | -387.247 | -1.00000 | -0.88714 | 1.67739 | -1.25367 | 0 | -0.46329 | 0 | 1.28991 | 0 | 0 | 0 | 0.27347 | |
| 2 | Intercept | COV | Normal | 0 Converged | -387.247 | -0.88714 | 0.13194 | -0.08735 | 0.05355 | 0 | 0.03029 | 0 | -0.06706 | 0 | 0 | 0 | -0.02807 | |
| 3 | dose | COV | Normal | 0 Converged | -387.247 | 1.67739 | -0.08735 | 0.06672 | -0.04751 | 0 | -0.03408 | 0 | 0.05862 | 0 | 0 | 0 | 0.01820 | |
| 4 | treatA | COV | Normal | 0 Converged | -387.247 | -1.25367 | 0.05355 | -0.04751 | 0.06843 | 0 | 0.03606 | 0 | -0.07532 | 0 | 0 | 0 | -0.01708 | |
| 5 | treatB | COV | Normal | 0 Converged | -387.247 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0 | 0.00000 | 0 | 0.00000 | 0 | 0 | 0 | 0.00000 | |
| 6 | sex0 | COV | Normal | 0 Converged | -387.247 | -0.46329 | 0.03029 | -0.03408 | 0.03606 | 0 | 0.05238 | 0 | -0.06360 | 0 | 0 | 0 | -0.00809 | |
| 7 | sex1 | COV | Normal | 0 Converged | -387.247 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0 | 0.00000 | 0 | 0.00000 | 0 | 0 | 0 | 0.00000 | |
| 8 | treatAsex0 | COV | Normal | 0 Converged | -387.247 | 1.28991 | -0.06706 | 0.05862 | -0.07532 | 0 | -0.06360 | 0 | 0.11941 | 0 | 0 | 0 | 0.01913 | |
| 9 | treatAsex1 | COV | Normal | 0 Converged | -387.247 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0 | 0.00000 | 0 | 0.00000 | 0 | 0 | 0 | 0.00000 | |
| 10 | treatBsex0 | COV | Normal | 0 Converged | -387.247 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0 | 0.00000 | 0 | 0.00000 | 0 | 0 | 0 | 0.00000 | |
| 11 | treatBsex1 | COV | Normal | 0 Converged | -387.247 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0 | 0.00000 | 0 | 0.00000 | 0 | 0 | 0 | 0.00000 | |
| 12 | _C_ | COV | Normal | 0 Converged | -387.247 | 0.27347 | -0.02807 | 0.01820 | -0.01708 | 0 | -0.00809 | 0 | 0.01913 | 0 | 0 | 0 | 0.00895 |
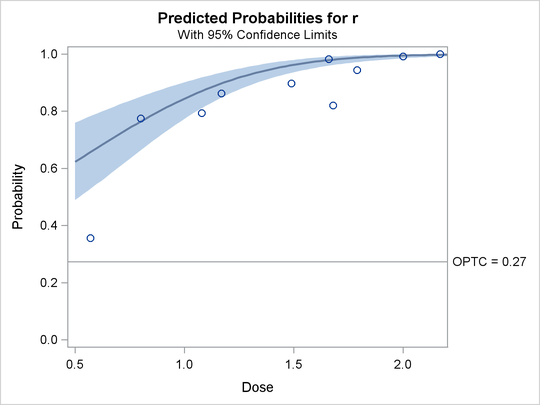
The plots in the following three outputs, Output 93.4.11, Output 93.4.12, and Output 93.4.13, are generated by the PLOTS= option. The first plot, specified with the PREDPPLOT option, is the plot of the predicted probability
against the first single continuous variable dose in the MODEL statement. You can specify values of other independent variables in the MODEL statement by using an XDATA= data
set or by using the default values.
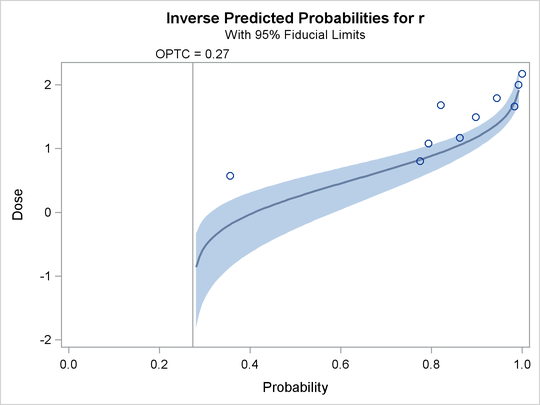
The second plot, specified with the IPPPLOT option, is the inverse of the predicted probability plot with the fiducial limits.
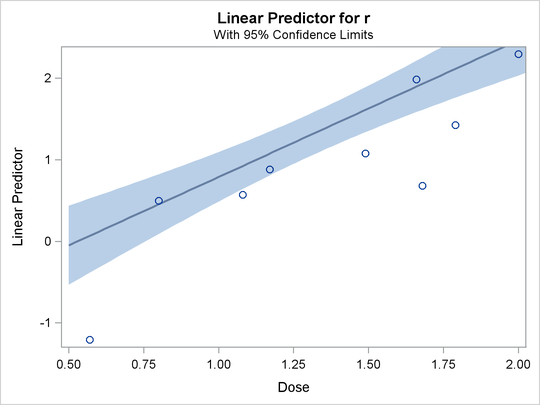
It should be pointed out that the fiducial limits are not just the inverse of the confidence limits in the predicted probability plot; see the section Inverse Confidence Limits for the computation of these limits. The third plot, specified with the LPREDPLOT option, is the plot of the linear predictor
 against the first single continuous variable with the Wald confidence intervals.
against the first single continuous variable with the Wald confidence intervals.
Output 93.4.11: Predicted Probability Plot
Output 93.4.12: Inverse Predicted Probability Plot
Output 93.4.13: Linear Predictor Plot