The PROBIT Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PROBIT StatementBY StatementCDFPLOT StatementCLASS StatementEFFECTPLOT StatementESTIMATE StatementINSET StatementIPPPLOT StatementLPREDPLOT StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementPREDPPLOT StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PROBIT StatementBY StatementCDFPLOT StatementCLASS StatementEFFECTPLOT StatementESTIMATE StatementINSET StatementIPPPLOT StatementLPREDPLOT StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementPREDPPLOT StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingComputational MethodDistributionsINEST= SAS-data-setModel SpecificationLack-of-Fit TestsRescaling the Covariance MatrixTolerance DistributionInverse Confidence LimitsOUTEST= SAS-data-setXDATA= SAS-data-setTraditional High-Resolution GraphicsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingComputational MethodDistributionsINEST= SAS-data-setModel SpecificationLack-of-Fit TestsRescaling the Covariance MatrixTolerance DistributionInverse Confidence LimitsOUTEST= SAS-data-setXDATA= SAS-data-setTraditional High-Resolution GraphicsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Example 93.3 Logistic Regression and Scoring New Data
In this example, a series of people are asked whether or not they would subscribe to a new newspaper. For each person, the
variables sex (Female, Male), age, and subs (1=yes, 0=no) are recorded. The PROBIT procedure is used to fit a logistic regression model to the probability of subscribing
(subs = 1) as a function of the variables sex and age. Specifically, the probability of subscribing is modeled as
![\[ p = \Pr ({\Variable{subs}}=1) = F \left( b_0 + b_1 \times {\Variable{sex}} + b_2 \times {\Variable{age}} \right) \]](images/statug_probit0097.png)
where F is the cumulative logistic distribution function.
By default, the PROBIT procedure models the probability of the lower response level. The following statements format the values
of subs as 1 = ’accept’ and 0 = ’reject’, and model 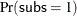 by using the EVENT= response variable option. The STORE statement saves the fitted model in an item store named LogitModel.
The results are shown in Output 93.3.1.
by using the EVENT= response variable option. The STORE statement saves the fitted model in an item store named LogitModel.
The results are shown in Output 93.3.1.
data news; input sex $ age subs @@; datalines; Female 35 0 Male 44 0 Male 45 1 Female 47 1 Female 51 0 Female 47 0 Male 54 1 Male 47 1 Female 35 0 Female 34 0 Female 48 0 Female 56 1 Male 46 1 Female 59 1 Female 46 1 Male 59 1 Male 38 1 Female 39 0 Male 49 1 Male 42 1 Male 50 1 Female 45 0 Female 47 0 Female 30 1 Female 39 0 Female 51 0 Female 45 0 Female 43 1 Male 39 1 Male 31 0 Female 39 0 Male 34 0 Female 52 1 Female 46 0 Male 58 1 Female 50 1 Female 32 0 Female 52 1 Female 35 0 Female 51 0 ;
proc format; value subscrib 1 = 'accept' 0 = 'reject'; run;
proc probit data=news; class sex; model subs(event="accept")=sex age / d=logistic itprint; format subs subscrib.; store out=LogitModel; run;
Output 93.3.1: Logistic Regression of Subscription Status
| Iteration History for Parameter Estimates | |||||
|---|---|---|---|---|---|
| Iter | Ridge | Loglikelihood | Intercept | sexFemale | age |
| 0 | 0 | -27.725887 | 0 | 0 | 0 |
| 1 | 0 | -20.142659 | -3.634567629 | -1.648455751 | 0.1051634384 |
| 2 | 0 | -19.52245 | -5.254865196 | -2.234724956 | 0.1506493473 |
| 3 | 0 | -19.490439 | -5.728485385 | -2.409827238 | 0.1639621828 |
| 4 | 0 | -19.490303 | -5.76187293 | -2.422349862 | 0.1649007124 |
| 5 | 0 | -19.490303 | -5.7620267 | -2.422407743 | 0.1649050312 |
| 6 | 0 | -19.490303 | -5.7620267 | -2.422407743 | 0.1649050312 |
| Analysis of Maximum Likelihood Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
95% Confidence Limits | Chi-Square | Pr > ChiSq | ||
| Intercept | 1 | -5.7620 | 2.7635 | -11.1783 | -0.3458 | 4.35 | 0.0371 | |
| sex | Female | 1 | -2.4224 | 0.9559 | -4.2959 | -0.5489 | 6.42 | 0.0113 |
| sex | Male | 0 | 0.0000 | . | . | . | . | . |
| age | 1 | 0.1649 | 0.0652 | 0.0371 | 0.2927 | 6.40 | 0.0114 | |
Output 93.3.1 shows that there appears to be an effect due to both the variables sex and age. The positive coefficient for age indicates that older people are more likely to subscribe than younger people. The negative coefficient for sex indicates that females are less likely to subscribe than males.
You can use the SCORE statement in the PLM procedure to score new observations based on the fitted model saved by the STORE
statement above. For example, to compute the probability of subscribing for one new observation with sex = ‘Female’ and age = 35 in the data set test, you can use the following statements:
data test; input sex $ age; datalines; Female 35 ;
proc plm restore=LogitModel; score data=test out=testout predicted / ilink; run; proc print data=testout; run;
The ILINK option in the SCORE statement applies the inverse of the logit link to provide an estimate on the mean (probability) scale. Output 93.3.2 shows the predicted probability for the new observation.
Output 93.3.2: Predicted Probability for One New Observation