The PROBIT Procedure
- Overview
-
Getting Started
-
SyntaxPROC PROBIT StatementBY StatementCDFPLOT StatementCLASS StatementEFFECTPLOT StatementESTIMATE StatementINSET StatementIPPPLOT StatementLPREDPLOT StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementPREDPPLOT StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
-
DetailsMissing ValuesResponse Level OrderingComputational MethodDistributionsINEST= SAS-data-setModel SpecificationLack-of-Fit TestsRescaling the Covariance MatrixTolerance DistributionInverse Confidence LimitsOUTEST= SAS-data-setXDATA= SAS-data-setTraditional High-Resolution GraphicsDisplayed OutputODS Table NamesODS Graphics
-
Examples
- References
Tolerance Distribution
For a single independent variable, such as a dosage level, the models for the probabilities can be justified on the basis
of a population with mean 
and scale parameter 
of tolerances for the subjects. Then, given a dose x, the probability, P, of observing a response in a particular subject is the probability that the subject’s tolerance is less than the dose or
![\[ P = F \left( \frac{x - \mu }{\sigma } \right) \]](images/statug_probit0081.png)
Thus, in this case, the intercept parameter, 
, and the regression parameter,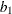 
, are related to and by
![\[ b_0 = -\frac{\mu }{\sigma }, b_1 = \frac{1}{\sigma } \]](images/statug_probit0084.png)
Note: The parameter is not equal to the standard deviation of the population of tolerances for the logistic and extreme value distributions.