The MIANALYZE Procedure

Example 76.11 Combining Correlation Coefficients

This example combines sample correlation coefficients that are computed from a set of imputed data sets by using Fisher’s z transformation.

Fisher’s z transformation of the sample correlation r is

$z = \frac{1}{2} \, \mr{log} \left( \frac{1+r}{1-r} \right)$

The statistic z is approximately normally distributed, with mean

$\mr{log} \left( \frac{1+\rho }{1-\rho } \right)$

and variance 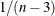$1/(n-3)$ , where 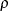$\rho$ is the population correlation coefficient and n is the number of observations.

The following statements use the CORR procedure to compute the correlation r and its associated Fisher’s z statistic between the variables Oxygen and RunTime for each imputed data set.

ods select none;
proc corr data=outmi fisher(biasadj=no);
   var Oxygen RunTime;
   by _Imputation_;
   ods output FisherPearsonCorr=outz;
run;
ods select all;

Because of the ODS SELECT statements, no output is displayed. The ODS OUTPUT statement is used to save Fisher’s z statistic in an output data set. The following statements display the number of observations and Fisher’s z statistic for each imputed data set in Output 76.11.1:

proc print data=outz (obs=10);
   title 'Fisher''s Correlation Statistics (First 10 Imputations)';
   var _Imputation_ NObs ZVal;
run;

Output 76.11.1: Output z Statistics

Fisher's Correlation Statistics (First 10 Imputations)

Obs	_Imputation_	NObs	ZVal
1	1	31	-1.27869
2	2	31	-1.30715
3	3	31	-1.27922
4	4	31	-1.39243
5	5	31	-1.40146
6	6	31	-1.22323
7	7	31	-1.27163
8	8	31	-1.17783
9	9	31	-1.36075
10	10	31	-1.23652

The following statements generate the standard error associated with the z statistic, 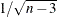$1/\sqrt {n-3}$ :

data outz;
   set outz;
   StdZ= 1. / sqrt(NObs-3);
run;

The following statements use the MIANALYZE procedure to generate a combined parameter estimate 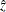$\hat{z}$ and its variance, as shown in Output 76.11.2. The ODS OUTPUT statement is used to save the parameter estimates in an output data set.

proc mianalyze data=outz;
   ods output ParameterEstimates=parms;
   modeleffects ZVal;
   stderr StdZ;
run;

Output 76.11.2: Combining Fisher’s z Statistics

The MIANALYZE Procedure

Parameter Estimates (25 Imputations)
Parameter	Estimate	Std Error	95% Confidence Limits		DF	Minimum	Maximum	Theta0	t for H0: Parameter=Theta0	Pr > \|t\|
ZVal	-1.292006	0.202699	-1.68963	-0.89438	1403.6	-1.401459	-1.098356	0	-6.37	<.0001

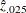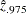In addition to the estimate for z, PROC MIANALYZE also generates 95% confidence limits for z, $\hat{z}_{.025}$ and $\hat{z}_{.975}$ . The following statements print the estimate and 95% confidence limits for z in Output 76.11.3:

proc print data=parms;
   title 'Parameter Estimates with 95% Confidence Limits';
   var Estimate LCLMean UCLMean;
run;

Output 76.11.3: Parameter Estimates with 95% Confidence Limits

Parameter Estimates with 95% Confidence Limits

Obs	Estimate	LCLMean	UCLMean
1	-1.292006	-1.68963	-0.89438

An estimate of the correlation coefficient with its corresponding 95% confidence limits is then generated from the following inverse transformation as described in the section Correlation Coefficients:

$r = \mr{tanh}(z) =\frac{e^{2z} - 1}{e^{2z} + 1}$

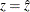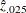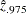for $z = \hat{z}$ , $\hat{z}_{.025}$ , and $\hat{z}_{.975}$ .

The following statements generate and display an estimate of the correlation coefficient and its 95% confidence limits, as shown in Output 76.11.4:

data corr_ci;
   set parms;
   r=       tanh( Estimate);
   r_lower= tanh( LCLMean);
   r_upper= tanh( UCLMean);
run;
proc print data=corr_ci;
   title 'Estimated Correlation Coefficient'
         ' with 95% Confidence Limits';
   var r r_lower r_upper;
run;

Output 76.11.4: Estimated Correlation Coefficient

Estimated Correlation Coefficient with 95% Confidence Limits

Obs	r	r_lower	r_upper
1	-0.85965	-0.93410	-0.71355