The MIANALYZE Procedure

Combining Inferences from Imputed Data Sets

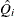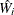With m imputations, m different sets of the point and variance estimates for a parameter Q can be computed. Suppose that $\hat{Q_ i}$ and $\hat{W_ i}$ are the point and variance estimates, respectively, from the ith imputed data set, i = 1, 2, …, m. Then the combined point estimate for Q from multiple imputation is the average of the m complete-data estimates:

\[ {\overline Q} = \frac{1}{m} \sum _{i=1}^{m} \hat{Q_ i} \]

Suppose that 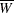${\overline W}$ is the within-imputation variance, which is the average of the m complete-data estimates:

\[ {\overline W} = \frac{1}{m} \sum _{i=1}^{m} \hat{W_ i} \]

And suppose that B is the between-imputation variance:

\[ B = \frac{1}{m-1} \sum _{i=1}^{m} (\hat{Q_ i}-{\overline Q})^2 \]

Then the variance estimate associated with 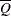${\overline Q}$ is the total variance (Rubin 1987)

\[ T = {\overline W} + (1+\frac{1}{m}) B \]

The statistic 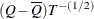$(Q-{\overline Q}) T^{-(1/2)}$ is approximately distributed as t with 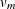$v_{m}$ degrees of freedom (Rubin 1987), where

\[ v_{m} = (m-1) {\left[ 1 + \frac{{\overline W}}{(1+m^{-1})B} \right]}^2 \]

The degrees of freedom 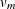$v_{m}$ depend on m and the ratio

\[ r = \frac{(1+m^{-1})B}{\overline W} \]

The ratio r is called the relative increase in variance due to nonresponse (Rubin 1987). When there is no missing information about Q, the values of r and B are both zero. With a large value of m or a small value of r, the degrees of freedom 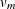$v_{m}$ will be large and the distribution of 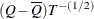$(Q-{\overline Q}) T^{-(1/2)}$ will be approximately normal.

Another useful statistic is the fraction of missing information about Q:

\[ \hat{\lambda } = \frac{r+2/(v_{m}+3)}{r+1} \]

Both statistics r and 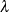$\lambda $ are helpful diagnostics for assessing how the missing data contribute to the uncertainty about Q.

When the complete-data degrees of freedom 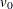$v_{0}$ are small, and there is only a modest proportion of missing data, the computed degrees of freedom, 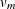$v_{m}$, can be much larger than 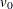$v_{0}$, which is inappropriate. For example, with m = 5 and r = 10%, the computed degrees of freedom 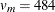$v_{m}=484$, which is inappropriate for data sets with complete-data degrees of freedom less than 484.

Barnard and Rubin (1999) recommend the use of adjusted degrees of freedom

\[ v_{m}^{*} = \, \left[ \frac{1}{v_{m}} + \frac{1}{\hat{v}_{\mathit{obs}}} \right] ^{-1} \]

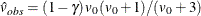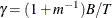where   $\hat{v}_{\mathit{obs}} = (1 - \gamma ) \, v_{0} (v_{0}+1) / (v_{0}+3)$   and   $\gamma = (1+m^{-1}) B / T$.

If you specify the complete-data degrees of freedom 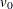$v_{0}$ with the EDF= option, the MIANALYZE procedure uses the adjusted degrees of freedom, 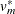$v_{m}^{*}$, for inference. Otherwise, the degrees of freedom 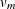$v_{m}$ are used.