The MIANALYZE Procedure

This example creates a DATA=EST data set to contain regression coefficients and their corresponding covariance matrices that are computed from imputed data sets. These estimates are then combined to generate valid statistical inferences about the regression model. A TEST statement is used to test linear hypotheses about the parameters.

The following statements use the REG procedure to generate regression coefficients for each imputed data set:

proc reg data=outmi outest=outreg covout noprint;
   model Oxygen= RunTime RunPulse;
   by _Imputation_;
run;

The following statements combine the results for the imputed data sets. A TEST statement is used to test linear hypotheses of INTERCEPT=0 and RUNTIME=RUNPULSE.

proc mianalyze data=outreg edf=28;
   modeleffects Intercept RunTime RunPulse;
   test Intercept, RunTime=RunPulse / mult;
run;

The "Test Specification" table in Output 76.10.1 displays the matrix and the vector in a TEST statement. Because no label is specified for the TEST statement, "Test 1" is used as the label.

The "Variance Information" table in Output 76.10.2 displays the between-imputation variance, within-imputation variance, and total variance for each univariate inference. A detailed description of these statistics is provided in the section Combining Inferences from Imputed Data Sets and the section Multiple Imputation Efficiency.

The "Parameter Estimates" table in Output 76.10.3 displays the estimated mean and standard error of the linear components. The inferences are based on the t distribution. The table also displays a 95% mean confidence interval and a t test along with the associated p-value for the hypothesis that each linear component of 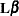is equal to 0.

When you specify the MULT option, PROC MIANALYZE assumes that the between-imputation covariance matrix is proportional to the within-imputation covariance matrix and displays a multivariate inference for all the linear components that are taken jointly in Output 76.10.4.