The MIANALYZE Procedure
- Overview
- Getting Started
-
Syntax

-
Details

-
Examples
 Reading Means and Standard Errors from a DATA= Data SetReading Means and Covariance Matrices from a DATA= COV Data SetReading Regression Results from a DATA= EST Data SetReading Mixed Model Results from PARMS= and COVB= Data SetsReading Generalized Linear Model ResultsReading GLM Results from PARMS= and XPXI= Data SetsReading Logistic Model Results from a PARMS= Data SetReading Mixed Model Results with Classification CovariatesReading Nominal Logistic Model ResultsUsing a TEST statementCombining Correlation CoefficientsSensitivity Analysis with Control-Based Pattern ImputationSensitivity Analysis with the Tipping-Point Approach
Reading Means and Standard Errors from a DATA= Data SetReading Means and Covariance Matrices from a DATA= COV Data SetReading Regression Results from a DATA= EST Data SetReading Mixed Model Results from PARMS= and COVB= Data SetsReading Generalized Linear Model ResultsReading GLM Results from PARMS= and XPXI= Data SetsReading Logistic Model Results from a PARMS= Data SetReading Mixed Model Results with Classification CovariatesReading Nominal Logistic Model ResultsUsing a TEST statementCombining Correlation CoefficientsSensitivity Analysis with Control-Based Pattern ImputationSensitivity Analysis with the Tipping-Point Approach - References
Examples of the Complete-Data Inferences
For a given parameter of interest, it is not always possible to compute the estimate and associated covariance matrix directly from a SAS procedure. This section describes examples of parameters with their estimates and associated covariance matrices, which provide the input to the MIANALYZE procedure. Some are straightforward, and others require special techniques.
Means
For a population mean vector 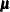 , the usual estimate is the sample mean vector
, the usual estimate is the sample mean vector
![\[ \overline{\mb{y}} = \frac{1}{n} \sum {\mb{y}_{i}} \]](images/statug_mianalyze0071.png)
A variance estimate for 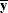 is
is 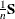 , where
, where 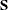 is the sample covariance matrix
is the sample covariance matrix
![\[ \mb{S} = \frac{1}{\, n-1 \, } \sum { ( \mb{y}_{i} - \overline{\mb{y}} ) ( \mb{y}_{i} - \overline{\mb{y}} )’ } \]](images/statug_mianalyze0075.png)
These statistics can be computed from a procedure such as PROC CORR. This approach is illustrated in Example 76.2.
Regression Coefficients
Many SAS procedures are available for regression analysis. Among them, PROC REG provides the most general analysis capabilities, and others like PROC LOGISTIC and PROC MIXED provide more specialized analyses.
Some regression procedures, such as REG and LOGISTIC, create an EST type data set that contains both the parameter estimates for the regression coefficients and their associated covariance matrix. You can read an EST type data set in the MIANALYZE procedure with the DATA= option. This approach is illustrated in Example 76.3.
Other procedures, such as GLM, MIXED, and GENMOD, do not generate EST type data sets for regression coefficients. For PROC MIXED and PROC GENMOD, you can use ODS OUTPUT statement to save parameter estimates in a data set and the associated covariance matrix in a separate data set. These data sets are then read in the MIANALYZE procedure with the PARMS= and COVB= options, respectively. This approach is illustrated in Example 76.4 for PROC MIXED and in Example 76.5 for PROC GENMOD.
PROC GLM does not display tables for covariance matrices. However, you can use the ODS OUTPUT statement to save parameter
estimates and associated standard errors in a data set and the associated 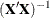 matrix in a separate data set. These data sets are then read in the MIANALYZE procedure with the PARMS= and XPXI= options,
respectively. This approach is illustrated in Example 76.6.
matrix in a separate data set. These data sets are then read in the MIANALYZE procedure with the PARMS= and XPXI= options,
respectively. This approach is illustrated in Example 76.6.
For univariate inference, only parameter estimates and associated standard errors are needed. You can use the ODS OUTPUT statement to save parameter estimates and associated standard errors in a data set. This data set is then read in the MIANALYZE procedure with the PARMS= option. This approach is illustrated in Example 76.4.
Correlation Coefficients
For the population correlation coefficient 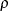 , a point estimate is the sample correlation coefficient r. However, for nonzero
, a point estimate is the sample correlation coefficient r. However, for nonzero 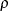 , the distribution of r is skewed.
, the distribution of r is skewed.
The distribution of r can be normalized through Fisher’s z transformation
![\[ z(r) = \frac{1}{2} \, \mr{log} \left( \frac{1+r}{1-r} \right) \]](images/statug_mianalyze0077.png)
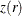 is approximately normally distributed with mean
is approximately normally distributed with mean 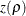 and variance
and variance 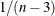 .
.
With a point estimate 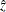 and an approximate 95% confidence interval
and an approximate 95% confidence interval 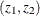 for
for 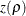 , a point estimate
, a point estimate 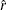 and a 95% confidence interval
and a 95% confidence interval 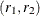 for
for 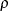 can be obtained by applying the inverse transformation
can be obtained by applying the inverse transformation
![\[ r = \mr{tanh}(z) = \frac{e^{2z} - 1}{e^{2z} + 1} \]](images/statug_mianalyze0085.png)
to 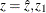 , and
, and 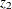 .
.
This approach is illustrated in Example 76.11.
Ratios of Variable Means
For the ratio 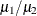 of means for variables
of means for variables 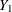 and
and 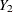 , the point estimate is
, the point estimate is 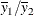 , the ratio of the sample means. The Taylor expansion and delta method can be applied to the function
, the ratio of the sample means. The Taylor expansion and delta method can be applied to the function 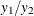 to obtain the variance estimate (Schafer 1997, p. 196)
to obtain the variance estimate (Schafer 1997, p. 196)
![\[ \frac{1}{n} \left[ {\left( \frac{\overline{y}_{1}}{\overline{y}_{2}^{2}} \right)}^{2} s_{22} - 2 {\left( \frac{\overline{y}_{1}}{y_{2}^{2}} \right)} {\left( \frac{1}{\overline{y}_{2}} \right)} s_{12} + {\left( \frac{1}{\overline{y}_{2}} \right)}^{2} s_{11} \right] \]](images/statug_mianalyze0093.png)
where 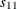 and
and 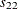 are the sample variances of
are the sample variances of 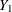 and
and 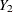 , respectively, and
, respectively, and 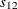 is the sample covariance between
is the sample covariance between 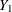 and
and 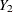 .
.
A ratio of sample means will be approximately unbiased and normally distributed if the coefficient of variation of the denominator (the standard error for the mean divided by the estimated mean) is 10% or less (Cochran 1977, p. 166; Schafer 1997, p. 196).