The ICPHREG Procedure

Overview: ICPHREG Procedure

Subsections:

The ICPHREG procedure is designed to fit proportional hazards regression models to interval-censored data. It can also fit proportional hazards regression models to failure time data that are uncensored, right censored, or left censored. The survival time of each member of a population is assumed to follow its own hazard function, 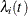$\lambda _{i}(t)$, which is expressed as

\[ \lambda _{i}(t)=\lambda (t;{\bZ }_{i}) = {\lambda _0}(t) \ \mr{exp}({\bZ }’_{i}\bbeta ) \]

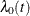where $\lambda _{0}(t)$ is the baseline hazard function, 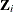${\bZ }_ i$ is the vector of explanatory variables for the ith individual, and 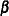$\bbeta $ is the vector of unknown regression coefficients that is associated with the explanatory variables. The vector 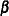$\bbeta $ is assumed to be the same for all individuals.

The ICPHREG procedure enables you to use a variety of configurations with respect to the baseline function to fit a proportional hazards model; these configurations include a piecewise constant model (Friedman 1982) and a cubic spline model (Royston and Parmar 2002). To estimate the regression coefficients and the baseline parameters, the ICPHREG procedure maximizes the full likelihood instead of the Cox partial likelihood. Standard errors of the estimates are obtained by inverting the observed information matrix, which is derived from the full likelihood.

The ICPHREG procedure also enables you to do the following: include an offset variable in the model, weight the observations in the input data, test linear hypotheses about the regression coefficients, compute customized hazard ratios, and estimate and plot the survival function and the cumulative hazard function for a new set of covariates.

The ICPHREG procedure uses ODS Graphics to create graphs as part of its output. For general information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS.