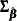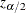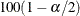The ICPHREG Procedure
Hazard Ratios
Consider a dichotomous risk factor variable X that takes the value 1 if the risk factor is present and 0 if the risk factor is absent. The log-hazard function is
![\[ \log [\lambda (t|X)] = \log [\lambda _0(t)] + \beta _1 X \]](images/statug_icphreg0129.png)
where 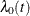 is the baseline hazard function.
is the baseline hazard function.
The hazard ratio 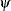 is defined as the ratio of the hazard for those who have the risk factor (X = 1) to the hazard for those who do not have the risk factor (X = 0). The log of the hazard ratio is
is defined as the ratio of the hazard for those who have the risk factor (X = 1) to the hazard for those who do not have the risk factor (X = 0). The log of the hazard ratio is
![\[ \log (\psi ) \equiv \log [\psi (X=1,X=0)] = \log [\lambda (t|X=1)] - \log [\lambda (t|X=0)] = \beta _1 \]](images/statug_icphreg0131.png)
In general, the hazard ratio can be computed by exponentiating the difference of the log-hazard between any two population
profiles. This is the approach taken by the HAZARDRATIO statement
, so the computations are available regardless of parameterization, interactions, and nestings. However, as shown in the preceding
equation for 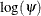 , hazard ratios of main effects can be computed as functions of the parameter estimates. The remainder of this section is
concerned with this methodology.
, hazard ratios of main effects can be computed as functions of the parameter estimates. The remainder of this section is
concerned with this methodology.
The parameter 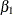 that is associated with X represents the change in the
log-hazard from X = 0 to X = 1. So the hazard ratio is obtained by simply exponentiating the value of the parameter that is associated with the risk
factor. The hazard ratio indicates how the hazard changes as you change X from 0 to 1. For example,
that is associated with X represents the change in the
log-hazard from X = 0 to X = 1. So the hazard ratio is obtained by simply exponentiating the value of the parameter that is associated with the risk
factor. The hazard ratio indicates how the hazard changes as you change X from 0 to 1. For example, 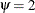 means that the hazard when X = 1 is twice the hazard when X = 0.
means that the hazard when X = 1 is twice the hazard when X = 0.
Suppose the values of the dichotomous risk factor are coded as constants a and b instead of 0 and 1. The hazard when 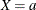 becomes
becomes 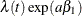 , and the hazard when
, and the hazard when 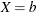 becomes
becomes 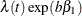 . The hazard ratio that corresponds to an increase in X from a to b is
. The hazard ratio that corresponds to an increase in X from a to b is
![\[ \psi = \exp [(b - a) \beta _1] = [\exp (\beta _1)]^{b-a} \equiv [\exp (\beta _1)]^ c \]](images/statug_icphreg0139.png)
Note that for any a and b such that 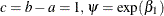 . So the hazard ratio can be interpreted as the change in the hazard for any increase of one unit in the corresponding risk
factor. However, the change in hazard for some amount other than one unit is often of greater interest. For example, a change
of one pound in body weight might be too small to be considered important, whereas a change of 10 pounds might be more meaningful.
The hazard ratio for a change in X from a to b is estimated by raising the hazard ratio estimate for a unit change in X to the power of
. So the hazard ratio can be interpreted as the change in the hazard for any increase of one unit in the corresponding risk
factor. However, the change in hazard for some amount other than one unit is often of greater interest. For example, a change
of one pound in body weight might be too small to be considered important, whereas a change of 10 pounds might be more meaningful.
The hazard ratio for a change in X from a to b is estimated by raising the hazard ratio estimate for a unit change in X to the power of 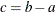 as shown previously.
as shown previously.
For a polytomous risk factor, the computation of hazard ratios depends on how the risk factor is parameterized. For illustration,
suppose that Cell is a risk factor that has four categories: Adeno, Large, Small, and Squamous.
For the effect parameterization scheme (PARAM=
EFFECT) with Squamous as the reference group, the design variables for Cell are as follows:
|
Design Variables |
|||
|---|---|---|---|
|
|
|
|
|
|
Adeno |
1 |
0 |
0 |
|
Large |
0 |
1 |
0 |
|
Small |
0 |
0 |
1 |
|
Squamous |
–1 |
–1 |
–1 |
The log-hazard for Adeno is
![\begin{eqnarray*} \log [\lambda (t|\mbox{Adeno})] & =& \log [\lambda _0(t)] + \beta _1 (X_1=1) + \beta _2 (X_2=0) + \beta _3 (X_3=0) \\ & =& \lambda _0(t) + \beta _1 \end{eqnarray*}](images/statug_icphreg0145.png)
The log-hazard for Squamous is
![\begin{eqnarray*} \log [\lambda (t|\mbox{Squamous})] & =& \log [\lambda _0(t)] + \beta _1 (X_1=-1) + \beta _2 (X_2=-1)+ \beta _3 (X_3=-1)) \\ & =& \log [\lambda _0(t)] - \beta _1 - \beta _2 - \beta _3 \end{eqnarray*}](images/statug_icphreg0146.png)
Therefore, the log-hazard ratio of Adeno versus Squamous
![\begin{eqnarray*} \log [\psi (\mbox{Adeno},\mbox{Squamous})] & =& \log [\lambda (t|\mbox{Adeno})] - \log [\lambda (t|\mbox{Squamous})] \\ & =& 2 \beta _1 + \beta _2 + \beta _3 \end{eqnarray*}](images/statug_icphreg0147.png)
For the reference cell parameterization scheme (PARAM=
REF) in which Squamous is the reference cell, the design variables for Cell are as follows:
|
Design Variables |
|||
|---|---|---|---|
|
|
|
|
|
|
Adeno |
1 |
0 |
0 |
|
Large |
0 |
1 |
0 |
|
Small |
0 |
0 |
1 |
|
Squamous |
0 |
0 |
0 |
The log-hazard ratio of Adeno versus Squamous is
![\begin{eqnarray*} \lefteqn{\log (\psi (\mbox{Adeno},\mbox{Squamous}))} \\ & = & \log [\lambda (t|\mbox{Adeno})] - \log [\lambda (t|\mbox{Squamous})] \\ & = & (\log [\lambda _0(t)] + \beta _1 (X_1=1) + \beta _2 (X_2=0) + \beta _3 (X_3=0)) - \\ & & (\log [\lambda _0(t)] + \beta _1 (X_1=0) + \beta _2 (X_2=0) + \beta _3 (X_3=0)) \\ & = & \beta _1 \end{eqnarray*}](images/statug_icphreg0148.png)
For the GLM parameterization scheme (PARAM= GLM), the design variables are as follows:
|
Design Variables |
||||
|---|---|---|---|---|
|
|
|
|
|
|
|
Adeno |
1 |
0 |
0 |
0 |
|
Large |
0 |
1 |
0 |
0 |
|
Small |
0 |
0 |
1 |
0 |
|
Squamous |
0 |
0 |
0 |
1 |
The log-hazard ratio of Adeno versus Squamous is
![\begin{eqnarray*} \lefteqn{\log (\psi (\mbox{Adeno},\mbox{Squamous}))} \\ & = & \log [\lambda (t|\mbox{Adeno})] - \log [\lambda (t|\mbox{Squamous})] \\ & = & \log [\lambda _0(t)] + \beta _1 (X_1=1) + \beta _2 (X_2=0) + \beta _3 (X_3=0) + \beta _4 (X_4=0)) -\\ & & (\log (\lambda _0(t)) + \beta _1 (X_1=0) + \beta _2 (X_2=0) + \beta _3 (X_3=0) + \beta _4(X_4=1)) \\ & = & \beta _1 - \beta _4 \end{eqnarray*}](images/statug_icphreg0150.png)
Consider Cell as the only risk factor. The computation of the hazard ratio of Adeno versus Squamous for various parameterization schemes
is shown in Table 63.7.
Table 63.7: Hazard Ratio of Adeno to Squamous
|
Parameter Estimates |
|||||
|---|---|---|---|---|---|
|
PARAM= |
|
|
|
|
Hazard Ratio Estimates |
|
EFFECT |
0.5772 |
–0.2115 |
0.2454 |
|
|
|
REF |
1.8830 |
0.3996 |
0.8565 |
|
|
|
GLM |
1.8830 |
0.3996 |
0.8565 |
0.0000 |
|
The fact that the log-hazard ratio (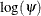 ) is a linear function of the parameters enables the HAZARDRATIO statement
to compute the hazard ratio of the main effect even in the presence of interactions and nest effects.
) is a linear function of the parameters enables the HAZARDRATIO statement
to compute the hazard ratio of the main effect even in the presence of interactions and nest effects.
To customize hazard ratios for specific units of change for a continuous risk factor, you can use the UNITS=
option in a HAZARDRATIO statement
to specify a list of relevant units for each explanatory variable in the model. Estimates of these customized hazard ratios
are shown in a separate table. Let  be a confidence interval for
be a confidence interval for 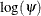 . The corresponding lower and upper confidence limits for the customized hazard ratio
. The corresponding lower and upper confidence limits for the customized hazard ratio 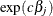 are
are 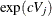 and
and 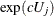 , respectively for
, respectively for 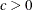 , or
, or 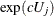 and
and 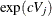 , respectively for
, respectively for 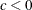 .
.
Let 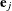 be the jth unit vector—that is, the jth entry of the vector is 1 and all other entries are 0. The hazard ratio for the explanatory variable with regression coefficient
be the jth unit vector—that is, the jth entry of the vector is 1 and all other entries are 0. The hazard ratio for the explanatory variable with regression coefficient
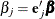 is defined as
is defined as 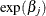 .
In general, a log-hazard ratio can be written as
.
In general, a log-hazard ratio can be written as 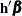 (a linear combination of the regression coefficients), and the hazard ratio
(a linear combination of the regression coefficients), and the hazard ratio 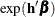 is obtained by replacing
is obtained by replacing 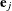 with
with 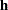 .
.
Point Estimate
The hazard ratio 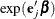 is estimated by
is estimated by 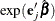 , where
, where 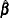 is the maximum likelihood estimate of the regression coefficients
is the maximum likelihood estimate of the regression coefficients 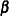 .
.

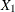
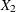
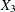
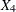
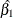
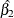
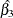
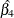
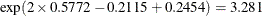
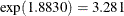
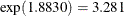
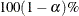
![\[ \mr{exp} \left(\mb{e}_ j’ \hat{\bbeta } \pm z_{\alpha /2} \sqrt {\mb{e}_ j’\bSigma _{\hat{\bbeta }}\mb{e}_ j} \right) \]](images/statug_icphreg0171.png)