The ICPHREG Procedure

Model and Likelihood

Suppose that the observations to be analyzed consist of interval-censored outcomes $\{ [L_ i, R_ i]; \bZ _ i\}$ , $i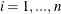=1,...,n$ , where n is the number of subjects. 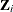$\bZ _ i$ denotes a p-dimensional vector of covariates for the ith subject. This notation allows for exact event times, right-censored data and left-censored data as special cases. When 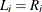$L_ i=R_ i$ , the observation is an exact time; when 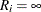$R_ i=\infty$ , the observation is right-censored; when 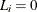$L_ i=0$ , the observation is left-censored.

Let 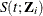$S(t;\bZ _ i)$ denote the survival function for a subject whose covariate is 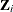$\bZ _ i$ . Assuming that t is continuous, denote 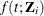$f(t;\bZ _ i)$ as the density function for the subject. The hazard function for the subject, 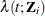$\lambda (t;\bZ _ i)$ , is defined as the instantaneous failure rate at time t. Mathematically, the hazard function is determined as a ratio between the density function and the survival function:

$\lambda (t;\bZ _ i)=f(t;\bZ _ i)/S(t;\bZ _ i)$

A quantity that is closely related to the survival function is the cumulative hazard function, defined as

$\Lambda (t;\bZ _ i)=\int _0^ t \lambda (u;\bZ _ i)\, du$

In turn, the cumulative hazard function determines the survival function:

$S(t;\bZ _ i) = \exp (-\Lambda (t;\bZ _ i))$

If some of the responses are left-, right-, or interval-censored, the log likelihood can be written as

$\begin{eqnarray*} \mr{log(L)} & =& \sum \log \left[ f(L_ i;\bZ _ i) \right] + \sum \log \left[ S(L_ i;\bZ _ i) \right] \\ & +& \sum \log \left[ 1 - S(R_ i;\bZ _ i) \right] + \sum \log \left[ S(L_ i;\bZ _ i) - S(R_ i;\bZ _ i) \right] \end{eqnarray*}$

where the first sum is the total of the uncensored observations, the second sum is the total of the right-censored observations, the third sum is the total of the left-censored observations, and the last sum is the total of the interval-censored observations.

For the ith subject, the proportional hazards model (Cox 1972) assumes that

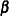$\lambda (t;\bZ _ i) = \lambda _0(t) \exp (\bZ _ i’ \bbeta )$

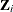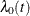where $\bbeta$ is a p-dimensional vector of coefficients for the covariate vector $\bZ _ i$ and $\lambda _0(t)$ is the baseline hazard function, which is the hazard rate when all the coefficients for the covariates are equal to 0.

Under the proportional hazards model, the cumulative hazard function for the ith subject is

$\Lambda (t;\bZ _ i) = \int _0^ t \lambda (u;\bZ _ i)\, du = \int _0^ t \lambda _0(u)\, du \exp (\bZ _ i’\bbeta ) = \Lambda _0(t) \exp (\bZ _ i’\bbeta )$

The survival function for the ith subject is

$S(t;\bZ _ i) = \exp [-\Lambda (t;\bZ _ i)] = S_0(t)^{\exp (\bZ _ i'\bbeta )}$

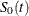where $S_0(t)$ denotes the baseline survival function and $S_0(t)=\exp [-\Lambda _0(t)]$ .

The density function for the subject is obtained by differentiating the survival function:

$f(t;\bZ _ i) = -\frac{d S(t;\bZ _ i)}{dt} = \lambda (t;\bZ _ i) S(t;\bZ _ i) = \lambda _0(t) \exp (\bZ _ i’\bbeta ) S_0(t)^{\exp (\bZ _ i'\bbeta )}$

Given these quantities, the likelihood function under the proportional hazards model can be expressed as

$\begin{eqnarray*} \mr{log(L)} & =& \sum \log \left[ \lambda _0(L_ i)\exp (\bZ _ i’\bbeta ) S_0(L_ i)^{\exp (\bZ _ i'\bbeta )} \right] + \sum \log \left[ S_0(L_ i)^{\exp (\bZ _ i'\bbeta )} \right] \\ & +& \sum \log \left[ 1 - S_0(R_ i)^{\exp (\bZ _ i'\bbeta )} \right] + \sum \log \left[ S_0(L_ i)^{\exp (\bZ _ i'\bbeta )} - S_0(R_ i)^{\exp (\bZ _ i'\bbeta )} \right] \end{eqnarray*}$

This likelihood function is often referred as the full likelihood as compared to the partial likelihood (Cox 1972) because it involves parameters for the baseline hazard function in addition to the regression coefficients 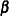$\bbeta$ . The full likelihood is often used for analyzing interval-censored data because constructing a likelihood function that contains only the regression coefficients as conveniently as the Cox partial likelihood does for right-censored data is not straightforward (Finkelstein 1986).