The ICPHREG Procedure
Computational Details
Design Matrix
The linear predictor part of a proportional hazards model is
![\[ \bm {\mu } = \mb{Z}’ \bbeta \]](images/statug_icphreg0081.png)
where 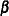 is a vector of unknown regression coefficients and
is a vector of unknown regression coefficients and 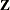 is a known design matrix.
The ordering of these parameters is displayed in the "CLASS Level Information" table and in tables that display the parameter
estimates of the fitted model.
is a known design matrix.
The ordering of these parameters is displayed in the "CLASS Level Information" table and in tables that display the parameter
estimates of the fitted model.
When you use the PARAM=
GLM option in the CLASS statement to specify an overparameterized model, some columns of 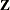 can be linearly dependent on other columns. For example, when you specify a model that consists of a classification variable,
the column that corresponds to any one of the levels of the classification variable is linearly dependent on the other columns
of
can be linearly dependent on other columns. For example, when you specify a model that consists of a classification variable,
the column that corresponds to any one of the levels of the classification variable is linearly dependent on the other columns
of 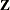 . The columns of
. The columns of 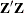 are checked in the order in which the model is specified for dependence on preceding columns. If a dependency is found, the
parameter that corresponds to the dependent column and its standard error are set to 0 to indicate that it is not estimated.
The test for linear dependence is controlled by the SINGULAR= option in the MODEL statement. You can use the ORDER=
option in the CLASS statement to specify the order in which the levels of a classification variable are checked for dependencies.
For full-rank parameterizations, the columns of the
are checked in the order in which the model is specified for dependence on preceding columns. If a dependency is found, the
parameter that corresponds to the dependent column and its standard error are set to 0 to indicate that it is not estimated.
The test for linear dependence is controlled by the SINGULAR= option in the MODEL statement. You can use the ORDER=
option in the CLASS statement to specify the order in which the levels of a classification variable are checked for dependencies.
For full-rank parameterizations, the columns of the 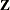 matrix are designed to be linearly independent.
matrix are designed to be linearly independent.
Initial Values
The initial values of the regression coefficients 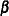 are all set to 0.
are all set to 0.
For the piecewise constant model, the initial values of the hazard parameters are set equal to the exponential rate that is
estimated from an imputed data set. The data set is obtained by imputing a middle point for the interval-censored and left-censored
observations while retaining the right-censored and exact observations. For the cubic spline model, the first spline coefficient,
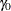 , is set to be the log of the exponential rate estimated with the previous imputed data, and the second spline coefficient,
, is set to be the log of the exponential rate estimated with the previous imputed data, and the second spline coefficient,
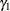 , is set to 1. The remaining spline coefficients, if there are any, are set to 0.
, is set to 1. The remaining spline coefficients, if there are any, are set to 0.
Maximum Likelihood Estimation
By default, the ICPHREG procedure uses a Newton-Raphson algorithm to maximize the log-likelihood function with respect to the parameters.
Denote the set of parameters that need to be estimated as 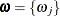 , which consists of the parameters that determine baseline hazard function
, which consists of the parameters that determine baseline hazard function 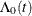 and the regression coefficients
and the regression coefficients 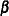 . On the rth iteration, the algorithm updates the parameter vector
. On the rth iteration, the algorithm updates the parameter vector 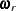 with
with
![\[ {\bomega }_{r+1} = {\bomega }_{r} - \mb{H}^{-1}\mb{g} \]](images/statug_icphreg0088.png)
where 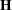 is the Hessian
(second derivative) matrix, and
is the Hessian
(second derivative) matrix, and 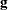 is the gradient
(first derivative) vector of the log-likelihood function, both evaluated at the current value of the parameter vector. That
is,
is the gradient
(first derivative) vector of the log-likelihood function, both evaluated at the current value of the parameter vector. That
is,
![\[ \mb{g} = [g_ j] = \left[ \frac{\partial l}{\partial \omega _ j} \right] \]](images/statug_icphreg0091.png)
and
![\[ \mb{H} = [{h_{ij}}] = \left[ \frac{\partial ^2 l}{\partial \omega _ i\partial \omega _ j} \right] \]](images/statug_icphreg0092.png)
The ICPHREG procedure also supports other optimization methods, such as quasi-Newton and Newton-Raphson with ridging. These methods are described in the section Choosing an Optimization Algorithm in Chapter 19: Shared Concepts and Topics.
Covariance and Correlation Matrix
The estimated covariance matrix of the parameter estimator is
![\[ \bSigma = -\mb{H}^{-1} \]](images/statug_icphreg0093.png)
where 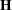 is the Hessian matrix that is evaluated using the parameter estimates on the last iteration. If some parameters in the baseline
function are held fixed, they are not incorporated in
is the Hessian matrix that is evaluated using the parameter estimates on the last iteration. If some parameters in the baseline
function are held fixed, they are not incorporated in 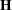 . Rows and columns that correspond to aliased parameters are not included in
. Rows and columns that correspond to aliased parameters are not included in 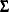 .
.
The correlation matrix
is the normalized covariance matrix. That is, if 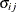 is an element of
is an element of 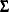 , then the corresponding element of the correlation matrix is
, then the corresponding element of the correlation matrix is 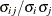 , where
, where 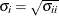 .
.
Choosing Break Points
There are no obvious ways to choose break points for parameterizing the baseline function in terms of a piecewise constant
function or a cubic spline curve. For right-censored data, PROC PHREG
chooses a set of points such that the resulting time intervals contain approximately equal numbers of event times. This is
difficult for interval-censored data because event times are not fully observed. Friedman (1982) recommends choosing the points so that the expected number of events is comparable among the time intervals. For an interval-censored
spline model, Cai and Betensky (2003) propose an ad hoc approach that uses the quantile values of the unique time points among 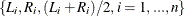 for choosing the knot values.
for choosing the knot values.
Ibrahim, Chen, and Sinha (2001) propose the equally spaced quantile partition (ESQP) method for selecting break points in the right-censored data to fit the piecewise constant model. Suppose there are Q break points to be determined. The ICPHREG procedure modifies this method to handle interval-censored data. First, it imputes a middle point for each observation that is not right-censored. Then, it merges these values with the observed boundary values in the input data set, except for the right-censored observations. Next, it sorts these values in increasing order.
Suppose the unique values of the sorted sequence are 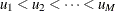 . First, PROC ICPHREG computes the targeted quantile for each break point as
. First, PROC ICPHREG computes the targeted quantile for each break point as 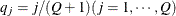 . Then, it chooses the point
. Then, it chooses the point 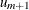 , where m equals the integer part of the product
, where m equals the integer part of the product 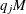 . If
. If 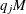 is already an integer, then the chosen break point is set to be
is already an integer, then the chosen break point is set to be 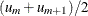 . When there are no ties in the sorted sequence for right-censored data, this method is identical to the original ESQP method.
. When there are no ties in the sorted sequence for right-censored data, this method is identical to the original ESQP method.
Fit Statistics
Suppose that the model contains q estimated parameters and that n observations are used in model fitting. The fit criteria displayed by the ICPHREG procedure are calculated as follows:
-
–2 log likelihood:
![\[ -2\mr{log(L)} \]](images/statug_icphreg0104.png)
where
 is the maximized likelihood for the model.
is the maximized likelihood for the model.
-
Akaike’s information criterion:
![\[ \mr{AIC}=-2\mr{log(L)}+2q \]](images/statug_icphreg0106.png)
-
corrected Akaike’s information criterion:
![\[ \mr{AICC}=\mr{AIC} + \frac{2q(q+1)}{n-q-1} \]](images/statug_icphreg0107.png)
-
Bayesian information criterion:
![\[ \mr{BIC}=-2\mr{log(L)}+q\log (n) \]](images/statug_icphreg0108.png)
For more information about AIC and BIC, see Akaike (1981, 1979). For a discussion of using AIC, AICC, and BIC in statistical modeling, see Simonoff (2003).
