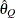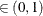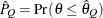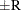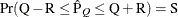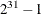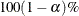-
ACCEPTTOL=n
-
specifies a tolerance for acceptance probabilities for the random walk sampler. By default, ACCEPTTOL=0.075. You can specify
this option for logit models.
-
ALGORITHM=GAMERMAN | RWM | LATENT
ALG=GAMERMAN | RWM | LATENT
-
specifies the algorithm to use to sample the posterior distribution for the regression coefficients. You can specify the following
algorithms:
-
GAMERMAN
-
uses the Metropolis-Hastings approach of Gamerman (1997). This is the default for logit models.
-
RWM
-
uses the random walk Metropolis algorithm along with the normal proposal, as suggested in Rossi, Allenby, and McCulloch (2005).
-
LATENT
-
uses the latent variables via the data augmentation method. This is the default for probit models. This option is ignored
for logit models.
When possible, PROC BCHOICE samples directly from the full conditional distribution. Otherwise, the default sampling algorithm
is the Gamerman algorithm for standard logit models, the random walk Metropolis algorithm for nested logit models, and the
latent variables via the data augmentation method for probit models. Standard logit models can also use random walk Metropolis
sampling algorithm if specified, while the other two types of models, nested logit models and probit models, have only their
own default sampling algorithm.
-
DATA=SAS-data-set
-
specifies the input data set.
-
DIAGNOSTICS=NONE | (keyword-list)
DIAG=NONE | (keyword-list)
-
specifies options for convergence diagnostics. By default, PROC BCHOICE computes the effective sample sizes. The sample autocorrelations,
Monte Carlo errors, Geweke test, Raftery-Lewis test, and Heidelberger-Welch test are also available. For more information
about convergence diagnostics, see the section Assessing Markov Chain Convergence in Chapter 7: Introduction to Bayesian Analysis Procedures. You can request all the diagnostic tests by specifying DIAGNOSTICS=ALL. You can suppress all the diagnostic tests by specifying
DIAGNOSTICS=NONE.
You can specify one or more of the following keyword-list options:
-
ALL
-
computes all diagnostic tests and statistics. You can combine the option ALL with any other specific tests to modify test
options. For example, DIAGNOSTICS=(ALL AUTOCORR(LAGS=(1 5 35))) computes all tests by using default settings and autocorrelations
at lags 1, 5, and 35.
-
AUTOCORR <(autocorrelation-options)>
AC <(autocorrelation-options)>
-
computes default autocorrelations at lags 1, 5, 10, and 50 for each variable. You can choose other lags by using the following
autocorrelation-option:
-
LAGS=(numeric-list)
-
specifies autocorrelation lags. The numeric-list must take positive integer values.
-
ESS
-
computes the effective sample sizes (Kass et al. 1998) of the posterior samples of each parameter. It also computes the correlation time and the efficiency of the chain for each
parameter. Small values of ESS might indicate a lack of convergence. For more information, see the section Effective Sample Size in Chapter 7: Introduction to Bayesian Analysis Procedures.
-
GEWEKE <(Geweke-options)>
-
computes the Geweke spectral density diagnostics; this is a two-sample t-test between the first 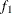 portion (as specified by the FRAC1= option) and the last
portion (as specified by the FRAC1= option) and the last 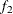 portion (as specified by the FRAC2= option) of the chain. For more information, see the section Geweke Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures. By default, FRAC1=0.1 and FRAC2=0.5, but you can choose other fractions by using the following Geweke-options:
portion (as specified by the FRAC2= option) of the chain. For more information, see the section Geweke Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures. By default, FRAC1=0.1 and FRAC2=0.5, but you can choose other fractions by using the following Geweke-options:
-
FRAC1=value
F1=value
-
specifies the beginning proportion of the Markov chain. By default, FRAC1=0.1.
-
FRAC2=value
F2=value
-
specifies the end proportion of the Markov chain. By default, FRAC2=0.5.
-
HEIDELBERGER <(Heidel-options)>
HEIDEL <(Heidel-options)>
-
computes the Heidelberger-Welch diagnostic (which consists of a stationarity test and a half-width test) for each variable.
The stationary diagnostic test tests the null hypothesis that the posterior samples are generated from a stationary process.
If the stationarity test is passed, a half-width test is then carried out. For more information, see the section Heidelberger and Welch Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures.
You can also specify suboptions, such as DIAGNOSTICS=HEIDELBERGER(EPS=0.05), as follows:
-
MAXLAG=n
-
specifies the maximum number of autocorrelation lags to use to compute the effective sample size; for more information, see
the section Effective Sample Size in Chapter 7: Introduction to Bayesian Analysis Procedures. The value of n is also used in the calculation of the Monte Carlo standard error; see the section Standard Error of the Mean Estimate in Chapter 7: Introduction to Bayesian Analysis Procedures. By default, MAXLAG=MIN(500, MCsample/4), where MCsample is the Markov chain sample size that is kept after thinning—that
is, MCsample ![$ = \left[ \frac{\mbox{NMC}}{\mbox{NTHIN}} \right] $](images/statug_bchoice0038.png) . If n is too low, you might observe significant lags and the effective sample size cannot be calculated accurately. A warning message
appears in the SAS log, and you can increase either the MAXLAG= option or the NMC=
option, accordingly. Specifying this option implies the ESS and MCSE options.
. If n is too low, you might observe significant lags and the effective sample size cannot be calculated accurately. A warning message
appears in the SAS log, and you can increase either the MAXLAG= option or the NMC=
option, accordingly. Specifying this option implies the ESS and MCSE options.
-
MCSE
MCERROR
-
computes the Monte Carlo standard error for the posterior samples of each parameter.
-
NONE
-
suppresses all the diagnostic tests and statistics. This option is not recommended.
-
RAFTERY <(Raftery-options)>
RL <(Raftery-options)>
-
computes the Raftery-Lewis diagnostic, which evaluates the accuracy of the estimated quantile (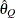 for a given Q
for a given Q 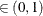 ) of a chain.
) of a chain. 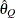 can achieve any degree of accuracy when the chain is allowed to run for a long time. The algorithm stops when the estimated
probability
can achieve any degree of accuracy when the chain is allowed to run for a long time. The algorithm stops when the estimated
probability 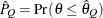 reaches within
reaches within 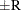 of the value Q with probability S; that is,
of the value Q with probability S; that is, 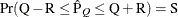 . For more information, see the section Raftery and Lewis Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures.
. For more information, see the section Raftery and Lewis Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures.
You can specify Q, R, S, and a precision level  for a stationary test by specifying the following Raftery-options—for example, DIAGNOSTICS=RAFTERY(QUANTILE=0.05):
for a stationary test by specifying the following Raftery-options—for example, DIAGNOSTICS=RAFTERY(QUANTILE=0.05):
-
ACCURACY=value
R=value
-
specifies a small positive number as the margin of error for measuring the accuracy of estimation of the quantile. By default,
ACCURACY=0.005.
-
EPS=value
-
specifies the tolerance level (a small positive number) for the stationary test. By default, EPS=0.001.
-
PROB=value
S=value
-
specifies the probability of attaining the accuracy of the estimation of the quantile. By default, PROB=0.95.
-
QUANTILE=value
Q=value
-
specifies the order (a value between 0 and 1) of the quantile of interest. By default, QUANTILE=0.025.
-
DIC
-
computes the deviance information criterion (DIC). DIC is calculated by using the posterior mean estimates of the parameters.
For more information, see the section Deviance Information Criterion (DIC) in Chapter 7: Introduction to Bayesian Analysis Procedures.
-
HITPROB
HITPROBABILITY
-
calculates the average of estimated probabilities of all chosen alternatives in the input data set. You can use this average
as a measure of goodness of fit.
-
INF=value
-
specifies the numerical definition of infinity in PROC BCHOICE. By default, INF=1E15. For example, PROC BCHOICE considers
1E16 to be outside the support of the normal distribution and assigns a missing value to the log density evaluation. The minimum
value that is allowed is 1E10, and the maximum value that is allowed is 1E27.
-
LOGPOST
-
calculates the logarithm of the posterior density of the parameters and the likelihood at each iteration. As a result, the
OUTPOST= data set will contain the LOGLIKE and LOGPOST variables. You can specify this option for logit models and nested
logit models, but not probit models.
-
MAXTUNE=n
-
specifies an upper limit for the number of proposal tuning loops for the random walk sampler. You can specify this option
for logit models; it is ignored for other models. By default, MAXTUNE=6.
-
MCHISTORY=BRIEF | DETAILED | NONE
MCHIST=BRIEF | DETAILED | NONE
-
controls the display of the Metropolis sampling history. This option is ignored for nested logit and probit models. You can
specify the following values:
-
BRIEF
-
produces a summary output for the tuning, burn-in, and sampling history tables. No tuning history table is produced if there
is no tuning stage. The tables show the following when applicable:
-
Scale shows the scale, or the range of the scales, that is used in each random walk Metropolis block that has a normal distribution.
-
Acceptance Rate shows the acceptance rate, or the range of the acceptance rates, for each Metropolis block.
-
DETAILED
-
produces detailed output of the tuning, burn-in, and sampling history tables, including scale values, acceptance probabilities,
and blocking information. No tuning history table is produced if there is no tuning stage. Use this option with caution, especially
in random-effects models that have a large number of random-effects groups, because it can produce copious output.
-
NONE
-
produces none of the tuning history, burn-in history, and sampling history tables.
By default, MCHISTORY=NONE.
-
MINTUNE=n
-
specifies a lower limit for the number of proposal tuning loops for the random walk sampler. You can specify this option for
logit models; it is ignored for other models. By default, MINTUNE=2.
-
NBI=n
-
specifies the number of burn-in iterations to perform before beginning to save parameter estimate chains. By default, NBI=500.
For more information, see the section Burn-In, Thinning, and Markov Chain Samples in Chapter 7: Introduction to Bayesian Analysis Procedures.
-
NMC=n
-
specifies the number of iterations in the main simulation loop. This is the MCMC sample size if THIN=
1. By default, NMC=5000.
-
NOCLPRINT<=n>
-
suppresses the display of the "Class Level Information" table if you do not specify n. If you specify n, the values of the classification variables are displayed for only those variables whose number of levels is less than n. Specifying n helps reduce the size of the "Class Level Information" table if some classification variables have a large number of levels.
-
NTHREADS=n
NTHREAD=n
-
specifies the number of threads for analytic computations and overrides the SAS system option THREADS | NOTHREADS. If you
do not specify the NTHREADS= option or if you specify NTHREADS=0, the default number of threads is 1.
-
NTU=n
-
specifies the number of iterations to use in each proposal tuning phase for the random walk sampler. You can specify this
option for logit models; it is ignored for other models. By default, NTU=500.
-
OUTPOST=SAS-data-set
OUT=SAS-data-set
-
specifies an output data set to contain the posterior samples of all parameters and the iteration numbers. It contains the
log of the posterior density (LOGPOST) and the log likelihood (LOGLIKE) if you specify the LOGPOST
option. By default, no OUTPOST= data set is created.
-
PLOTS <(global-plot-options)> <= plot-request <(options)>>
PLOTS <(global-plot-options)> <= (plot-request <(options)> <... plot-request <(options)>>)>
-
controls the display of diagnostic plots. You can request three types of plots: trace plots, autocorrelation function plots,
and kernel density plots. By default, the plots are displayed in panels unless you specify the global-plot-option UNPACK. Also, when you specify more than one type of plot, the plots are grouped by parameter unless you specify the global-plot-option GROUPBY=TYPE. When you specify only one plot-request, you can omit the parentheses around it, as shown in the following example:
plots=none
plots(unpack)=trace
plots=(trace density)
If ODS Graphics is enabled but you do not specify the PLOTS= option, then PROC BCHOICE produces, for each parameter, a panel
that contains the trace plot, the autocorrelation function plot, and the density plot. This is equivalent to specifying PLOTS=(TRACE
AUTOCORR DENSITY).
You can specify the following global-plot-options:
-
FRINGE
-
adds a fringe plot to the horizontal axis of the density plot.
-
GROUPBY=PARAMETER | TYPE
GROUP=PARAMETER | TYPE
-
specifies how the plots are grouped when there is more than one type of plot. By default, GROUPBY=PARAMETER. You can specify
the following values:
-
TYPE
-
groups the plots by type.
-
PARAMETER
-
groups the plots by parameter.
-
LAGS=n
-
specifies the number of autocorrelation lags that are used in plotting the ACF graph. By default, LAGS=50.
-
SMOOTH
-
smooths the trace plot by using a fitted penalized B-spline curve (Eilers and Marx 1996).
-
UNPACKPANEL
UNPACK
-
unpacks all paneled plots, so that each plot in a panel is displayed separately.
You can specify the following plot-requests:
-
ALL
-
requests all types of plots. PLOTS=ALL is equivalent to specifying PLOTS=(TRACE AUTOCORR DENSITY).
-
AUTOCORR
ACF
-
displays the autocorrelation function plots for the parameters.
-
DENSITY
D
KERNEL
K
-
displays the kernel density plots for the parameters.
-
NONE
-
suppresses the display of all plots.
-
TRACE
T
-
displays the trace plots for the parameters.
Consider a model that has four parameters, X1–X4. The following list shows which plots are produced for various option settings:
-
PLOTS=(TRACE AUTOCORR) displays the trace and autocorrelation plots for each parameter side by side, with two parameters per
panel:
|
Display 1
|
Trace(X1)
|
Autocorr(X1)
|
| |
Trace(X2)
|
Autocorr(X2)
|
|
Display 2
|
Trace(X3)
|
Autocorr(X3)
|
| |
Trace(X4)
|
Autocorr(X4)
|
-
PLOTS(GROUPBY=TYPE)=(TRACE AUTOCORR) displays all the paneled trace plots, followed by panels of autocorrelation plots:
|
Display 1
|
Trace(X1)
|
| |
Trace(X2)
|
|
Display 2
|
Trace(X3)
|
| |
Trace(X4)
|
|
Display 3
|
Autocorr(X1)
|
Autocorr(X2)
|
| |
Autocorr(X3)
|
Autocorr(X4)
|
-
PLOTS(UNPACK)=(TRACE AUTOCORR) displays a separate trace plot and a separate correlation plot, parameter by parameter:
|
Display 1
|
Trace(X1)
|
|
Display 2
|
Autocorr(X1)
|
|
Display 3
|
Trace(X2)
|
|
Display 4
|
Autocorr(X2)
|
|
Display 5
|
Trace(X3)
|
|
Display 6
|
Autocorr(X3)
|
|
Display 7
|
Trace(X4)
|
|
Display 8
|
Autocorr(X4)
|
-
PLOTS(UNPACK GROUPBY=TYPE)=(TRACE AUTOCORR) displays all the separate trace plots, followed by the separate autocorrelation
plots:
|
Display 1
|
Trace(X1)
|
|
Display 2
|
Trace(X2)
|
|
Display 3
|
Trace(X3)
|
|
Display 4
|
Trace(X4)
|
|
Display 5
|
Autocorr(X1)
|
|
Display 6
|
Autocorr(X2)
|
|
Display 7
|
Autocorr(X3)
|
|
Display 8
|
Autocorr(X4)
|
-
SCALE=value
-
controls the initial multiplicative scale to the covariance matrix of the proposal distribution for the random walk–based
Metropolis algorithm for logit models. By default, SCALE=2.93. For more information, see the section Scale Tuning.
-
SEED=n
-
specifies the random number seed. By default, SEED=0, and PROC BCHOICE gets a random number seed from the system clock. Negative
seed values are treated as the default. The largest possible value for the seed is 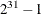 . Analyses that use the same nonzero seed are reproducible. The seed value is reported in the "Model Information" table.
. Analyses that use the same nonzero seed are reproducible. The seed value is reported in the "Model Information" table.
-
STATISTICS <(global-stats-options)> = NONE | ALL | stats-request
STATS <(global-stats-options)> = NONE | ALL | stats-request
-
specifies options for posterior statistics. By default, PROC BCHOICE computes the posterior mean, standard deviation, quantiles,
and two 95% credible intervals: equal-tail and highest posterior density (HPD). Other available statistics include the posterior
correlation and covariance. For more information, see the section Summary Statistics in Chapter 7: Introduction to Bayesian Analysis Procedures. You can request all the posterior statistics by specifying STATS=ALL. You can suppress all the calculations by specifying
STATS=NONE.
You can specify the following global-stats-options:
-
ALPHA=numeric-list
-
specifies the  level for the equal-tail and HPD intervals. The value of
level for the equal-tail and HPD intervals. The value of  must be between 0 and 0.5. By default, ALPHA=0.05.
must be between 0 and 0.5. By default, ALPHA=0.05.
-
PERCENT=numeric-list
PERCENTAGE=numeric-list
-
calculates the posterior percentages. The numeric-list contains values between 0 and 100. By default, PERCENTAGE=(25 50 75).
You can specify the following stats-requests:
-
ALL
-
computes all posterior statistics. You can combine the ALL option with any other options. For example, STATS(ALPHA=(0.02 0.05
0.1))=ALL computes all statistics by using the default settings and intervals at  levels of 0.02, 0.05, and 0.1.
levels of 0.02, 0.05, and 0.1.
-
BRIEF
-
computes the posterior means, standard deviations, and 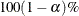 HPD credible interval for each variable. By default, ALPHA=0.05, but you can use the global ALPHA= option to request other
values. This is the default output for posterior statistics.
HPD credible interval for each variable. By default, ALPHA=0.05, but you can use the global ALPHA= option to request other
values. This is the default output for posterior statistics.
-
CORR
-
computes the posterior correlation matrix.
-
COV
-
computes the posterior covariance matrix.
-
INTERVAL
INT
-
computes the 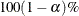 equal-tail and HPD credible intervals for each variable. For more information, see the sections Equal-Tail Credible Interval and Highest Posterior Density (HPD) Interval in Chapter 7: Introduction to Bayesian Analysis Procedures. By default, ALPHA=0.05, but you can use the global ALPHA= option to request other intervals of any probabilities.
equal-tail and HPD credible intervals for each variable. For more information, see the sections Equal-Tail Credible Interval and Highest Posterior Density (HPD) Interval in Chapter 7: Introduction to Bayesian Analysis Procedures. By default, ALPHA=0.05, but you can use the global ALPHA= option to request other intervals of any probabilities.
-
NONE
-
suppresses all the statistics.
-
SUMMARY
SUM
-
computes the posterior means, standard deviations, and percentile points for each variable. By default, the 25th, 50th, and
75th percentile points are produced, but you can use the global PERCENT= option to request specific percentile points.
-
TARGACCEPT=value
-
specifies the target acceptance rate for the random walk–based Metropolis algorithm for logit models. For more information,
see the section Metropolis and Metropolis-Hastings Algorithms in Chapter 7: Introduction to Bayesian Analysis Procedures. The numeric value must be between 0.01 and 0.99. By default, TARGACCEPT=0.45 for one parameter; TARGACCEPT=0.35 for two, three, or four parameters;
and TARGACCEPT=0.234 for more than four parameters (Roberts, Gelman, and Gilks; 1997; Roberts and Rosenthal; 2001).
-
THIN=n
NTHIN=n
-
controls the thinning rate of the simulation. PROC BCHOICE keeps every nth simulation sample and discards the rest. All posterior statistics and diagnostics are calculated by using the thinned samples.
By default, THIN=1. For more information, see the section Burn-In, Thinning, and Markov Chain Samples in Chapter 7: Introduction to Bayesian Analysis Procedures.
-
TUNEWT=value
-
specifies the multiplicative weight used in updating the covariance matrix of the proposal distribution for the random walk
sampler for logit models. The numeric value must be between 0 and 1. By default, TUNEWT=0.75. For more information, see the section Covariance Tuning.

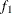
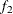


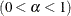
![$ = \left[ \frac{\mbox{NMC}}{\mbox{NTHIN}} \right] $](images/statug_bchoice0038.png)