The BCHOICE Procedure

RESTRICT Statement

RESTRICT <’label’> fixed-effect operand operator <value> ;

RESTRICT <’label’> fixed-effect constraint-list;

The RESTRICT statement enables you to specify restrictions on a fixed-effect that is specified in a preceding MODEL statement for a logit model. You can specify either a boundary requirement or order constraints on the fixed-effect. Specify one RESTRICT statement for each boundary requirement or order constraint. You must specify all boundary requirements before any order constraints. PROC BCHOICE incorporates the specified restrictions in the analysis. The RESTRICT statement is not available for a nested logit or probit model, nor for any random effects.

For either type of restriction, you can specify an optional label, surrounded by single quotation marks, and you must specify the following argument:

fixed-effect: specifies a fixed-effect that matches the one specified in the preceding MODEL statement. You can specify only one fixed-effect. Use multiple RESTRICT statements if you need to specify multiple restrictions for a single fixed-effect or if you need to specify restrictions on multiple fixed-effects.

Use the following syntax to specify a boundary requirement:

RESTRICT <’label’> fixed-effect operand operator <value> ;

You must specify the following arguments in addition to the fixed-effect:

operand: specifies what the operator applies to. For a continuous fixed-effect, specify 1; for a classification fixed-effect, specify a string of 0’s and one 1, where 1 indicates the level of the fixed-effect that the operator applies to.
operator: specifies one of the following mathematical operators: >, <, >=, <=.

You can also specify the following optional argument:

value: specifies a value to which the operator applies. The default is 0.

The following statements specify three boundary requirements:

proc bchoice;
   class Brand Subj;
   model choice = Brand Price / choiceset = (Subj);
   restrict Brand 1 0 0 0 > 0;
   restrict Brand 0 1 0 0 < 1;
   restrict Price 1 < -1;
run;

The first RESTRICT statement restricts the part-worth (regression coefficient) that is associated with the first level of the variable Brand to be positive. The second RESTRICT statement restricts the part-worth that is associated with the second level of the variable Brand to be less than 1. The third RESTRICT statement restricts the part-worth that is associated with the variable Price to be less than –1. You can specify a boundary restriction for only one parameter in one RESTRICT statement. If you want to specify both an upper bound and a lower bound for a parameter, use two RESTRICT statements.

Use the following syntax to specify an order constraint:

RESTRICT <’label’> fixed-effect constraint-list;

You must specify the following argument in addition to the fixed-effect:

constraint-list: specifies a list of order constraints for the classification variable that is specified in the preceding CLASS statement. The constraint-list can contain integers 0 through the total number of estimable levels for the classification variable, where 0 indicates a level that is ignored, 1 indicates the level that has the smallest part-worth (regression coefficient), 2 indicates the level that has the second-smallest part-worth, and so on.

In the following statements, the RESTRICT statement specifies that the first level of the variable Brand has the second-smallest part-worth, the second level has the smallest part-worth, the third level is ignored, and the fourth level has the largest part-worth:

proc bchoice;
   class Brand Subj;
   model choice = Brand Price / choiceset = (Subj);
   restrict Brand 2 1 0 3;
run;

Because reference coding is used, the fifth level of the variable is the reference level and is normalized to 0. No order index is needed for the reference level.

When you specify a constraint for a fixed-effect, the corresponding parameter is transformed to an unconstrained variable behind the scenes. The transformation is based on the constraint.

For example, if a fixed-effect 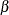$\beta$ is specified to have a lower bound a, then 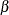$\beta$ is transformed to an unbounded variable $\alpha$ :

$\alpha = \log (\beta - a)$

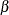The inverse of the lower-bound transformation maps an unbounded variable $\alpha$ to a variable $\beta$ that is bounded below by a:

$\beta = \exp (\alpha ) + a$

The normal prior distribution is assumed on the unconstrained parameters. PROC BCHOICE samples the unconstrained parameters first and then exponentiates the unconstrained parameters when they enter the utility function.

Suppose you specify the following order constraint on a set of fixed-effects:

$\beta _1 < \beta _2 < \ldots < \beta _ K$

PROC BCHOICE maps them to an unconstrained set of variables 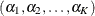$(\alpha _1, \alpha _2, \ldots , \alpha _ K)$ by setting

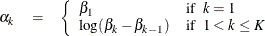
$\begin{eqnarray*} \alpha _{k}& =& \left\{ \begin{array}{ll} \beta _1 & \mbox{if}~ ~ k=1\\ \log (\beta _ k - \beta _{k-1}) & \mbox{if}~ ~ 1 < k \le K\\ \end{array}\right. \end{eqnarray*}$

Then, the inverse of this transformation is defined by the recursion:

$\begin{eqnarray*} \beta _{k}& =& \left\{ \begin{array}{ll} \alpha _1 & \mbox{if}~ ~ k=1\\ \exp (\alpha _ k) + \beta _{k-1} & \mbox{if}~ ~ 1 < k \le K\\ \end{array}\right. \end{eqnarray*}$