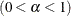The BCHOICE Procedure
Autocall Macros for Postprocessing
Although PROC BCHOICE provides a number of convergence diagnostic tests and posterior summary statistics, it performs the calculations only for the default tests and statistics or only if you specify the options in advance. If you want to analyze the posterior draws of unmonitored parameters or functions of the parameters that are calculated in later DATA step calls, you can use the autocall macros that are listed in Table 27.6.
Table 27.6: Postprocessing Autocall Macros
|
Macro |
Description |
|---|---|
|
%ESS |
Effective sample sizes |
|
%GEWEKE* |
Geweke diagnostic |
|
%HEIDEL* |
Heidelberger-Welch diagnostic |
|
%MCSE |
Monte Carlo standard errors |
|
%POSTACF |
Autocorrelation |
|
%POSTCOR |
Correlation matrix |
|
%POSTCOV |
Covariance matrix |
|
%POSTINT |
Equal-tail and HPD intervals |
|
%POSTSUM |
Summary statistics |
|
%RAFTERY |
Raftery diagnostic |
|
*The %GEWEKE and %HEIDEL macros use a different optimization routine than that used in PROC BCHOICE. As a result, there might be numerical differences in some cases, especially when the sample size is small. |
|
Table 27.7 lists options that are shared by all postprocessing autocall macros. For macro-specific options, see Table 27.8.
Table 27.7: Shared Options
|
Option |
Description |
|---|---|
|
DATA=SAS-data-set |
Names the input data set that contains posterior samples |
|
OUT=SAS-data-set |
Specifies a name for the output SAS data set to contain the results |
|
PRINT=YES | NO |
Displays the results (the default is YES) |
|
VAR=variable-list |
Specifies the variables on which to perform the calculation |
Suppose the data set that contains posterior samples is called Post and the variables of interest are defined in the macro variable &PARMS. The following statements call the %ESS macro and
calculate the effective sample sizes for each variable:
%ESS(data=Post, var=Alpha Beta U_1-U_17)
By default, the ESS estimates are displayed. You can choose not to display the result and instead use the following statement to save the output to a data set:
%ESS(data=Post, var=&parms, print=NO, out=eout)
Some of the macros can take additional options, which are listed in Table 27.8.
Table 27.8: Macro-Specific Options
|
Macro |
Option |
Description |
|---|---|---|
|
%ESS |
AUTOCORLAG=numeric |
Specifies the maximum number of autocorrelation lags used in computing the ESS estimates. By default, AUTOCORLAG=MIN(500, NOBS/4), where NOBS is the sample size of the input data set. |
|
HIST=YES | NO |
Displays a histogram of all ESS estimates. By default, HIST=NO. |
|
|
%GEWEKE |
FRAC1=numeric |
Specifies the earlier portion of the Markov chain used in the test. By default, FRAC1=0.1. |
|
FRAC2=numeric |
Specifies the latter portion of the Markov chain used in the test. By default, FRAC2=0.5. |
|
|
%HEIDEL |
SALPHA=numeric |
Specifies the |
|
HALPHA=numeric |
Specifies the |
|
|
EPS=numeric |
Specifies a small positive number |
|
|
%MCSE |
AUTOCORLAG=numeric |
Specifies the maximum number of autocorrelation lags used in computing the Monte Carlo standard error estimates. By default, AUTOCORLAG=MIN(500, NOBS/4), where NOBS is the sample size of the input data set. |
|
%POSTACF |
LAGS=%str(numeric-list) |
Specifies which autocorrelation lags to calculate. The default values are 1, 5, 10, and 50. |
|
%POSTINT |
ALPHA=value |
Specifies the |
|
%RAFTERY |
Q=numeric |
Specifies the order of the quantile of interest. By default, Q=0.025. |
|
R=numeric |
Specifies the margin of error for measuring the accuracy of estimation of the quantile. By default, R=0.005. |
|
|
S=numeric |
Specifies the probability of attaining the accuracy of the estimation of the quantile. By default, S=0.95. |
|
|
EPS=numeric |
Specifies the tolerance level for the stationary test. By default, EPS=0.001. |
For example, the following statement calculates and displays autocorrelation at lags 1, 6, 11, 50, and 100. Note that the lags in the numeric-list must be separated by commas.
%PostACF(data=Post, var=&parms, lags=%str(1 to 15 by 5, 50, 100))