The BCHOICE Procedure
Example 27.5 Heterogeneity Affected by Individual Characteristics
Rossi, Allenby, and McCulloch (2005) studied a scanner panel data about purchases of margarine. The data were first analyzed in Allenby and Rossi (1991) and are about purchases of ten brands of margarine. This example considers a subset of data about six margarine brands: Parkay stick, Blue Bonnet stick, Fleischmann’s stick, a house brand stick, a generic stick, and Shedd’s Spread tub. There are 313 households, which made a total of 3,405 purchases. Information about a few demographic characteristics of these households (income and family size) is expected to have effects on the central location of the distribution of heterogeneity.
The data set, which is called Sashelp.Margarin, comes from the SASHELP library.
proc print data=Sashelp.Margarin (obs=24); by HouseID Set; id HouseID Set; run;
The data for the first four choice sets are shown in Output 27.5.1.
Output 27.5.1: Data for the First Four Choice Sets
The variable HouseID represents the household ID, and each household made at least five purchases, which are defined by Set. The variable Choice represents the choice made among the six margarine brands for each purchase or choice set. The variable Brand has the value PPK for Parkay stick, PBB for Blue Bonnet stick, PFL for Fleischmann’s stick, PHse for the house brand stick,
PGen for the generic stick, and PSS for Shedd’s Spread tub. The variable LogPrice is the logarithm of the product price. The variables LogInc and variable FamSize provide information about household income and family size, respectively.
The following statements fit a random-effects-only logit model using Gamerman Metropolis sampling
proc bchoice data=Sashelp.Margarin seed=123 nmc=40000 thin=2 nthreads=4;
class Brand(ref='PPk') HouseID Set;
model Choice = / choiceset=(HouseID Set);
random Brand LogPrice / subject=HouseID remean=(LogInc FamSize)
type=un monitor=(1);
run;
The REMEAN=(LOGINC FAMSIZE)
option in the RANDOM
statement requests estimation of the nonzero mean of the random effects, which is a function of household income and family
size. No fixed effects are specified in the MODEL
statement. Summary statistics for the mean matrix of the random coefficients ( ), the covariance of the random coefficients (
), the covariance of the random coefficients (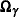 ), and the random coefficients (
), and the random coefficients (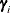 ) for the first household are shown in Output 27.5.2.
) for the first household are shown in Output 27.5.2.
Output 27.5.2: Posterior Summary Statistics
| Posterior Summaries and Intervals | ||||||
|---|---|---|---|---|---|---|
| Parameter | Subject | N | Mean | Standard Deviation |
95% HPD Interval | |
| REMean Brand PBB | 20000 | -1.2079 | 0.6384 | -2.4293 | 0.0686 | |
| REMean Brand PFl | 20000 | -3.2484 | 1.9276 | -7.0351 | 0.5201 | |
| REMean Brand PGen | 20000 | -5.1130 | 1.2332 | -7.6390 | -2.8030 | |
| REMean Brand PHse | 20000 | -3.2595 | 0.9194 | -5.0725 | -1.4761 | |
| REMean Brand PSS | 20000 | 0.0915 | 1.2127 | -2.3015 | 2.4981 | |
| REMean LogPrice | 20000 | -3.4148 | 0.8359 | -5.0397 | -1.7620 | |
| REMean Brand PBB LogInc | 20000 | 0.0529 | 0.2114 | -0.3485 | 0.4811 | |
| REMean Brand PFl LogInc | 20000 | 0.7596 | 0.6208 | -0.4726 | 1.9749 | |
| REMean Brand PGen LogInc | 20000 | -0.5079 | 0.4019 | -1.2977 | 0.2698 | |
| REMean Brand PHse LogInc | 20000 | 0.0315 | 0.3029 | -0.5949 | 0.5931 | |
| REMean Brand PSS LogInc | 20000 | -0.6315 | 0.4131 | -1.4645 | 0.1555 | |
| REMean LogPrice LogInc | 20000 | -0.2837 | 0.2817 | -0.8434 | 0.2631 | |
| REMean Brand PBB FamSize | 20000 | -0.0274 | 0.0959 | -0.2180 | 0.1572 | |
| REMean Brand PFl FamSize | 20000 | -0.7357 | 0.3059 | -1.3283 | -0.1267 | |
| REMean Brand PGen FamSize | 20000 | 0.5775 | 0.1824 | 0.2269 | 0.9428 | |
| REMean Brand PHse FamSize | 20000 | 0.2365 | 0.1357 | -0.0291 | 0.4997 | |
| REMean Brand PSS FamSize | 20000 | 0.0528 | 0.1974 | -0.3347 | 0.4425 | |
| REMean LogPrice FamSize | 20000 | 0.1010 | 0.1273 | -0.1542 | 0.3424 | |
| RECov Brand PBB, Brand PBB | 20000 | 2.2081 | 0.3730 | 1.5261 | 2.9615 | |
| RECov Brand PFl, Brand PBB | 20000 | 1.8598 | 0.9106 | 0.1374 | 3.6776 | |
| RECov Brand PFl, Brand PFl | 20000 | 12.0894 | 3.9050 | 5.5544 | 20.0864 | |
| RECov Brand PGen, Brand PBB | 20000 | 1.9842 | 0.5697 | 0.8563 | 3.0829 | |
| RECov Brand PGen, Brand PFl | 20000 | 1.3300 | 1.9065 | -2.4622 | 5.1401 | |
| RECov Brand PGen, Brand PGen | 20000 | 8.3897 | 1.4835 | 5.5924 | 11.3433 | |
| RECov Brand PHse, Brand PBB | 20000 | 1.5148 | 0.4402 | 0.6799 | 2.3928 | |
| RECov Brand PHse, Brand PFl | 20000 | 2.1554 | 1.3869 | -0.5797 | 4.9030 | |
| RECov Brand PHse, Brand PGen | 20000 | 5.7576 | 0.9570 | 3.8799 | 7.6015 | |
| RECov Brand PHse, Brand PHse | 20000 | 5.4834 | 0.8441 | 3.9355 | 7.1970 | |
| RECov Brand PSS, Brand PBB | 20000 | 1.1860 | 0.6287 | -0.0412 | 2.4223 | |
| RECov Brand PSS, Brand PFl | 20000 | 0.6096 | 1.9471 | -3.0709 | 4.6460 | |
| RECov Brand PSS, Brand PGen | 20000 | 4.8189 | 1.1738 | 2.5960 | 7.1020 | |
| RECov Brand PSS, Brand PHse | 20000 | 3.4484 | 0.8805 | 1.7068 | 5.1649 | |
| RECov Brand PSS, Brand PSS | 20000 | 8.7098 | 1.8047 | 5.4222 | 12.2276 | |
| RECov LogPrice, Brand PBB | 20000 | -0.2260 | 0.3462 | -0.8764 | 0.4813 | |
| RECov LogPrice, Brand PFl | 20000 | 2.1909 | 0.9010 | 0.5220 | 4.0796 | |
| RECov LogPrice, Brand PGen | 20000 | -0.9989 | 0.6371 | -2.2175 | 0.2793 | |
| RECov LogPrice, Brand PHse | 20000 | -0.4254 | 0.5043 | -1.3751 | 0.6150 | |
| RECov LogPrice, Brand PSS | 20000 | 0.1734 | 0.6757 | -1.1897 | 1.4765 | |
| RECov LogPrice, LogPrice | 20000 | 2.1279 | 0.5373 | 1.1697 | 3.2261 | |
| Brand PBB | HouseID 2100016 | 20000 | -2.3546 | 1.0548 | -4.4528 | -0.3948 |
| Brand PFl | HouseID 2100016 | 20000 | -3.9792 | 2.7840 | -9.4491 | 0.9694 |
| Brand PGen | HouseID 2100016 | 20000 | -6.5984 | 1.6472 | -9.8601 | -3.4056 |
| Brand PHse | HouseID 2100016 | 20000 | -2.9722 | 1.2014 | -5.5148 | -0.8522 |
| Brand PSS | HouseID 2100016 | 20000 | -3.3807 | 2.1701 | -7.4577 | 0.7600 |
| LogPrice | HouseID 2100016 | 20000 | -4.6129 | 1.2361 | -6.9996 | -2.1437 |
Table 27.11 collects the posterior means and standard deviations of 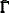 that are shown in Output 27.5.2. The first column corresponds to the parameters that are specified in the model, namely the brands and price. The second
column shows the average part-worths of each brand (versus the brand, Parkay stick) and the price at
that are shown in Output 27.5.2. The first column corresponds to the parameters that are specified in the model, namely the brands and price. The second
column shows the average part-worths of each brand (versus the brand, Parkay stick) and the price at LogInc=0 and FamSize=0. The LogInc and FamSize columns list the modifying effects on the preference for each brand and price by household income
and family size, respectively. Larger families show more interest in the generic and house brands and tend to stay away from
the Fleischmann’s brand. For example, consider the part-worth estimates for Fleischmann’s. The posterior mean for REMean Brand PFI FamSize (the Fleischmann’s row and the Famsize column) is –0.74 with a standard deviation of 0.31, meaning that an additional unit increase in family size is associated
with a reduction of 0.74 in the estimated part-worth for Fleischmann’s. In general, the demographics of households are only
weakly associated with preference for brand and price. These results are in good agreement with those of Rossi, Allenby, and
McCulloch (2005).
Table 27.11: Posterior Mean and Standard Deviation of 
|
Parameter |
Intercept |
LogInc |
FamSize |
|
|---|---|---|---|---|
|
Blue |
REMean Brand PBB |
REMean Brand PBB LogInc |
REMean Brand PBB FamSize |
|
|
Bonnet |
–1.21 |
0.05 |
–0.03 |
|
|
0.64 |
0.21 |
0.10 |
||
|
Fleisch- |
REMean Brand PFI |
REMean Brand PFI LogInc |
REMean Brand PFI FamSize |
|
|
mann’s |
–3.25 |
0.76 |
–0.74 |
|
|
1.93 |
0.62 |
0.31 |
||
|
REMean Brand PGen |
REMean Brand PGen LogInc |
REMean Brand PGen FamSize |
||
|
Generic |
–5.11 |
–0.51 |
0.58 |
|
|
1.23 |
0.40 |
0.18 |
||
|
REMean Brand PHse |
REMean Brand PHse LogInc |
REMean Brand PHse FamSize |
||
|
House |
–3.26 |
0.03 |
0.24 |
|
|
0.92 |
0.30 |
0.14 |
||
|
Shedd’s |
REMean Brand PSS |
REMean Brand PSS LogInc |
REMean Brand PSS FamSize |
|
|
Spread |
0.09 |
–0.63 |
–0.05 |
|
|
1.21 |
0.41 |
0.20 |
||
|
REMean LogPrice |
REMean LogPrice LogInc |
REMean LogPrice FamSize |
||
|
LogPrice |
–3.41 |
–0.28 |
0.10 |
|
|
0.84 |
0.28 |
0.13 |
Because the demographic variables are not zero-centered, the Intercept column shows the average part-worths of each brand
and price for households with LogInc=0 and FamSize=0, which are not very meaningful. It is better to center demographic variables by their means, so that the posterior means
listed in the Intercept column can be interpreted as the part-worths of a household that has an average income and average
size.
Nevertheless, you can obtain the utilities of households that have any income levels and sizes. For example, the average part-worth
of the Fleischmann’s brand for a household with average income (LogInc=3.1) and family size (FamSize=3) would be as follows, because the estimated LogInc coefficient is 0.76 and the estimated FamSize coefficient is –0.74 for Fleischmann’s:
![\[ -3.25+0.76\times 3.1-0.74\times 3=-3.11 \]](images/statug_bchoice0216.png)
You can obtain part-worths for all other brands and compare their popularity among average households.
The posterior means and standard deviations of the covariance matrix of the random coefficients (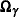 ) are displayed by parameters that are labeled "RECov Brand PBB, Brand PBB," "RECov Brand PFI, Brand PBB," and so on. Some
of the diagonal terms are fairly large, indicating that there is quite a bit of heterogeneity between households in margarine
brand preference and price sensitivity. The covariance between the generic and house brands, "RECov Brand PHse, Brand PGen,"
is fairly large, suggesting that household preferences for these two brands are highly correlated.
) are displayed by parameters that are labeled "RECov Brand PBB, Brand PBB," "RECov Brand PFI, Brand PBB," and so on. Some
of the diagonal terms are fairly large, indicating that there is quite a bit of heterogeneity between households in margarine
brand preference and price sensitivity. The covariance between the generic and house brands, "RECov Brand PHse, Brand PGen,"
is fairly large, suggesting that household preferences for these two brands are highly correlated.
The next set of parameters, which are displayed in Output 27.5.2, contain the estimates for the random effects for the first household.
