The BCHOICE Procedure

Tuning the Random Walk Metropolis in Logit Models

Subsections:

When you use a random walk Metropolis for a logit model, you want to find a good proposal distribution for each sampling block (for a fixed-effects block or for each individual random-effects block). This process is called tuning. The tuning phase consists of a number of loops. The minimum number of loops is controlled by the MINTUNE= option, which has a default value of 2. The MAXTUNE= option controls the maximum number of tuning loops, and it has a default value of 6. The number of iterations in each loop is controlled by the NTU= option, which has a default value of 500. At the end of every loop, PROC BCHOICE examines the acceptance probability for each block. The acceptance probability is the percentage of proposals (one from each iteration) that have been accepted. If the probability falls within the acceptance tolerance range (see the section Scale Tuning), the current configuration of the scale and covariance matrix is kept. Otherwise, the scale and covariance matrix are modified before the next tuning loop.

A good proposal distribution should resemble the actual posterior distribution of the parameters. Large-sample theory states that the posterior distribution of the parameters approaches a multivariate normal distribution (Gelman et al.; 2004, Appendix B; Schervish; 1995, Section 7.4). That is why a normal proposal distribution often works well in practice. The default proposal distribution in PROC BCHOICE is the normal distribution:

\[ q_ j(\theta _{\mbox{new}} | \theta ^ t) = \mbox{MVN} (\theta _{\mbox{new}} | \theta ^ t, c^2 \bSigma ) \]

Scale Tuning

The acceptance rate is closely related to the sampling efficiency of a Metropolis chain. For a random walk Metropolis, a high acceptance rate means that most new samples occur very close to the current data point. Their frequent acceptance means that the Markov chain is moving rather slowly and not exploring the parameter space fully. On the other hand, a low acceptance rate means that the proposed samples are often rejected; hence the chain is not moving much. An efficient Metropolis sampler has an acceptance rate that is neither too high nor too low. The scale c in the proposal distribution 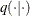$q(\cdot | \cdot )$ effectively controls this acceptance probability. Roberts, Gelman, and Gilks (1997) showed that if both the target and proposal densities are normal, the optimal acceptance probability for the Markov chain should be around 0.45 in a single-dimensional problem, and asymptotically approaches 0.234 in higher dimensions.

The nature of stochastic simulations makes it impossible to fine-tune a set of variables such that the Metropolis chain has the exact desired acceptance rate. In addition, Roberts and Rosenthal (2001) empirically demonstrate that an acceptance rate between 0.15 and 0.5 is at least 80% efficient, so there is really no need to fine-tune the algorithms to reach an acceptance probability that is within small tolerance of the optimal values. PROC BCHOICE works with a probability range, which is 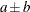$a\pm b$, where a and b are the values of the TARGACCEPT and ACCEPTTOL options, respectively, in the BCHOICE statement. The default value of TARGACCEPT is a function of the number of parameters in the model, as outlined in Roberts, Gelman, and Gilks (1997). By default, ACCEPTTOL= 0.075. If the observed acceptance rate in a particular tuning loop is less than the lower bound of the range, the scale is reduced; if the observed acceptance rate is greater than the upper bound of the range, the scale is increased. During the tuning phase, a scale parameter in the normal distribution is adjusted as a function of the observed acceptance rate and the target acceptance rate. PROC BCHOICE uses the updating scheme

\[ c_{\mbox{new}} =\frac{ c_{\mbox{cur}} \cdot \Phi ^{-1}( p_{\mbox{opt}}/2) }{ \Phi ^{-1}( p_{ \mbox{cur}}/2) } \]

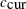where $c_{\mbox{cur}}$ is the current scale, 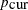$p_{\mbox{cur}}$ is the current acceptance rate, and 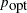$p_{\mbox{opt}}$ is the optimal acceptance probability.[24]

Covariance Tuning

To tune a covariance matrix, PROC BCHOICE takes a weighted average of the old proposal covariance matrix and the recently observed covariance matrix, based on a number of samples in the current loop that is specified in NTU= option. The TUNEWT=w option determines how much weight is put on the recently observed covariance matrix. The following formula is used to update the covariance matrix:

\[ \mbox{COV}_{\mbox{new}} = {\Argument{w}} ~ \mbox{COV}_{\mbox{cur}} + (1 - {\Argument{w}}) \mbox{COV}_{\mbox{old}} \]

For fixed effects:

  • By default, PROC BCHOICE uses the mode of the posterior density as the initial value of the fixed parameter and uses a numerical optimization routine (such as the quasi-Newton method) to find a starting covariance matrix. The optimization is performed on the joint posterior distribution, and the covariance matrix is a quadratic approximation at the posterior mode. In some cases, this is a better and more efficient way of initializing the covariance matrix. However, there are cases (such as when the number of parameters is large) where the optimization could fail to find a matrix that is positive definite. In that case, the tuning covariance matrix is reset to the identity matrix.

  • If you specify INIT=PRIORMODE or INIT=(LIST=numeric-list) to assign some initial values for the fixed effects in the MODEL statement, no numerical optimization is carried out and the proposal covariance matrix is set to the identity matrix divided by the number of parameters in the fixed effects sampling block. It can take a number of tuning phases before the proposal distribution is tuned to its optimal stage, because the Markov chain needs to spend time learning about the posterior covariance structure. If the posterior variances of your parameters vary by more than a few orders of magnitude, if the variances of your parameters are much different from 1, or if the posterior correlations are high, then the proposal tuning algorithm might have difficulty with forming an acceptable proposal distribution.

For random effects, the initial values are set to 0 and the proposal covariance matrix is set to the identity matrix divided by the number of parameters in each individual-level random-effects sampling block.


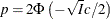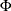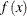[24] Roberts, Gelman, and Gilks (1997) and Roberts and Rosenthal (2001) demonstrate that the relationship between acceptance probability and scale in a random walk Metropolis is $p =2\Phi \left( -\sqrt {I} c /2\right)$, where $c $ is the scale, p is the acceptance rate, $\Phi $ is the CDF of a standard normal, and $I\equiv E_{f}[ ( f^{\prime } (x) /f (x) ) ^{2} ] $, $ f\left( x\right) $ is the density function of samples. This relationship determines the updating scheme, with I being replaced by the identity matrix to simplify calculation.