The MIXED Procedure
Example 58.5 Random Coefficients
This example comes from a pharmaceutical stability data simulation performed by Obenchain (1990). The observed responses are replicate assay results, expressed in percent of label claim, at various shelf ages, expressed in months. The desired mixed model involves three batches of product that differ randomly in intercept (initial potency) and slope (degradation rate). This type of model is also known as a hierarchical or multilevel model (Singer 1998; Sullivan, Dukes, and Losina 1999).
The SAS statements are as follows:
data rc;
input Batch Month @@;
Monthc = Month;
do i = 1 to 6;
input Y @@;
output;
end;
datalines;
1 0 101.2 103.3 103.3 102.1 104.4 102.4
1 1 98.8 99.4 99.7 99.5 . .
1 3 98.4 99.0 97.3 99.8 . .
1 6 101.5 100.2 101.7 102.7 . .
1 9 96.3 97.2 97.2 96.3 . .
1 12 97.3 97.9 96.8 97.7 97.7 96.7
2 0 102.6 102.7 102.4 102.1 102.9 102.6
2 1 99.1 99.0 99.9 100.6 . .
2 3 105.7 103.3 103.4 104.0 . .
2 6 101.3 101.5 100.9 101.4 . .
2 9 94.1 96.5 97.2 95.6 . .
2 12 93.1 92.8 95.4 92.2 92.2 93.0
3 0 105.1 103.9 106.1 104.1 103.7 104.6
3 1 102.2 102.0 100.8 99.8 . .
3 3 101.2 101.8 100.8 102.6 . .
3 6 101.1 102.0 100.1 100.2 . .
3 9 100.9 99.5 102.2 100.8 . .
3 12 97.8 98.3 96.9 98.4 96.9 96.5
;
proc mixed data=rc; class Batch; model Y = Month / s; random Int Month / type=un sub=Batch s; run;
In the DATA step, Monthc is created as a duplicate of Month in order to enable both a continuous and a classification version of the same variable. The variable Monthc is used in a subsequent analysis
In the PROC MIXED statements, Batch is listed as the only classification variable. The fixed effect Month in the MODEL statement is not declared as a classification variable; thus it models a linear trend in time. An intercept is included as a fixed effect by default, and the S option requests that the fixed-effects parameter estimates be produced.
The two random effects are Int and Month, modeling random intercepts and slopes, respectively. Note that Intercept and Month are used as both fixed and random effects. The TYPE=UN option in the RANDOM statement specifies an unstructured covariance matrix for the random intercept and slope effects. In mixed model notation, 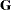 is block diagonal with unstructured 2
is block diagonal with unstructured 2 2 blocks. Each block corresponds to a different level of Batch, which is the SUBJECT= effect. The unstructured type provides a mechanism for estimating the correlation between the random coefficients. The S option requests the production of the random-effects parameter estimates.
2 blocks. Each block corresponds to a different level of Batch, which is the SUBJECT= effect. The unstructured type provides a mechanism for estimating the correlation between the random coefficients. The S option requests the production of the random-effects parameter estimates.
The results from this analysis are shown in Output 58.5.1–Output 58.5.9. The "Unstructured" covariance structure in Output 58.5.1 applies to  here.
here.
| Model Information | |
|---|---|
| Data Set | WORK.RC |
| Dependent Variable | Y |
| Covariance Structure | Unstructured |
| Subject Effect | Batch |
| Estimation Method | REML |
| Residual Variance Method | Profile |
| Fixed Effects SE Method | Model-Based |
| Degrees of Freedom Method | Containment |
Batch is the only classification variable in this analysis, and it has three levels (Output 58.5.2).
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| Batch | 3 | 1 2 3 |
The "Dimensions" table in Output 58.5.3 indicates that there are three subjects (corresponding to batches). The 24 observations not used correspond to the missing values of Y in the input data set.
| Dimensions | |
|---|---|
| Covariance Parameters | 4 |
| Columns in X | 2 |
| Columns in Z Per Subject | 2 |
| Subjects | 3 |
| Max Obs Per Subject | 36 |
| Number of Observations | |
|---|---|
| Number of Observations Read | 108 |
| Number of Observations Used | 84 |
| Number of Observations Not Used | 24 |
As Output 58.5.4 shows, only one iteration is required for convergence.
| Iteration History | |||
|---|---|---|---|
| Iteration | Evaluations | -2 Res Log Like | Criterion |
| 0 | 1 | 367.02768461 | |
| 1 | 1 | 350.32813577 | 0.00000000 |
| Convergence criteria met. |
The Estimate column in Output 58.5.5 lists the estimated elements of the unstructured 2 2 matrix comprising the blocks of
2 matrix comprising the blocks of 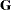 . Note that the random coefficients are negatively correlated.
. Note that the random coefficients are negatively correlated.
| Covariance Parameter Estimates | ||
|---|---|---|
| Cov Parm | Subject | Estimate |
| UN(1,1) | Batch | 0.9768 |
| UN(2,1) | Batch | -0.1045 |
| UN(2,2) | Batch | 0.03717 |
| Residual | 3.2932 | |
The null model likelihood ratio test indicates a significant improvement over the null model consisting of no random effects and a homogeneous residual error (Output 58.5.6).
| Fit Statistics | |
|---|---|
| -2 Res Log Likelihood | 350.3 |
| AIC (smaller is better) | 358.3 |
| AICC (smaller is better) | 358.8 |
| BIC (smaller is better) | 354.7 |
| Null Model Likelihood Ratio Test | ||
|---|---|---|
| DF | Chi-Square | Pr > ChiSq |
| 3 | 16.70 | 0.0008 |
The fixed-effects estimates represent the estimated means for the random intercept and slope, respectively (Output 58.5.7).
| Solution for Fixed Effects | |||||
|---|---|---|---|---|---|
| Effect | Estimate | Standard Error | DF | t Value | Pr > |t| |
| Intercept | 102.70 | 0.6456 | 2 | 159.08 | <.0001 |
| Month | -0.5259 | 0.1194 | 2 | -4.41 | 0.0478 |
The random-effects estimates represent the estimated deviation from the mean intercept and slope for each batch (Output 58.5.8). Therefore, the intercept for the first batch is close to 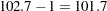 , while the intercepts for the other two batches are greater than 102.7. The second batch has a slope less than the mean slope of
, while the intercepts for the other two batches are greater than 102.7. The second batch has a slope less than the mean slope of 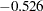 , while the other two batches have slopes greater than
, while the other two batches have slopes greater than 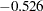 .
.
| Solution for Random Effects | ||||||
|---|---|---|---|---|---|---|
| Effect | Batch | Estimate | Std Err Pred | DF | t Value | Pr > |t| |
| Intercept | 1 | -1.0010 | 0.6842 | 78 | -1.46 | 0.1474 |
| Month | 1 | 0.1287 | 0.1245 | 78 | 1.03 | 0.3047 |
| Intercept | 2 | 0.3934 | 0.6842 | 78 | 0.58 | 0.5669 |
| Month | 2 | -0.2060 | 0.1245 | 78 | -1.65 | 0.1021 |
| Intercept | 3 | 0.6076 | 0.6842 | 78 | 0.89 | 0.3772 |
| Month | 3 | 0.07731 | 0.1245 | 78 | 0.62 | 0.5365 |
The F statistic in the "Type 3 Tests of Fixed Effects" table in Output 58.5.9 is the square of the t statistic used in the test of Month in the preceding "Solution for Fixed Effects" table (compare Output 58.5.7 and Output 58.5.9). Both statistics test the null hypothesis that the slope assigned to Month equals 0, and this hypothesis can barely be rejected at the 5% level.
| Type 3 Tests of Fixed Effects | ||||
|---|---|---|---|---|
| Effect | Num DF | Den DF | F Value | Pr > F |
| Month | 1 | 2 | 19.41 | 0.0478 |
It is also possible to fit a random coefficients model with error terms that follow a nested structure (Fuller and Battese 1973). The following SAS statements represent one way of doing this:
proc mixed data=rc; class Batch Monthc; model Y = Month / s; random Int Month Monthc / sub=Batch s; run;
The variable Monthc is added to the CLASS and RANDOM statements, and it models the nested errors. Note that Month and Monthc are continuous and classification versions of the same variable. Also, the TYPE=UN option is dropped from the RANDOM statement, resulting in the default variance components model instead of correlated random coefficients. The results from this analysis are shown in Output 58.5.10.
| Model Information | |
|---|---|
| Data Set | WORK.RC |
| Dependent Variable | Y |
| Covariance Structure | Variance Components |
| Subject Effect | Batch |
| Estimation Method | REML |
| Residual Variance Method | Profile |
| Fixed Effects SE Method | Model-Based |
| Degrees of Freedom Method | Containment |
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| Batch | 3 | 1 2 3 |
| Monthc | 6 | 0 1 3 6 9 12 |
| Dimensions | |
|---|---|
| Covariance Parameters | 4 |
| Columns in X | 2 |
| Columns in Z Per Subject | 8 |
| Subjects | 3 |
| Max Obs Per Subject | 36 |
| Number of Observations | |
|---|---|
| Number of Observations Read | 108 |
| Number of Observations Used | 84 |
| Number of Observations Not Used | 24 |
| Iteration History | |||
|---|---|---|---|
| Iteration | Evaluations | -2 Res Log Like | Criterion |
| 0 | 1 | 367.02768461 | |
| 1 | 4 | 277.51945360 | . |
| 2 | 1 | 276.97551718 | 0.00104208 |
| 3 | 1 | 276.90304909 | 0.00003174 |
| 4 | 1 | 276.90100316 | 0.00000004 |
| 5 | 1 | 276.90100092 | 0.00000000 |
| Convergence criteria met. |
| Covariance Parameter Estimates | ||
|---|---|---|
| Cov Parm | Subject | Estimate |
| Intercept | Batch | 0 |
| Month | Batch | 0.01243 |
| Monthc | Batch | 3.7411 |
| Residual | 0.7969 | |
For this analysis, the Newton-Raphson algorithm requires five iterations and nine likelihood evaluations to achieve convergence. The missing value in the Criterion column in iteration 1 indicates that a boundary constraint has been dropped.
The estimate for the Intercept variance component equals 0. This occurs frequently in practice and indicates that the restricted likelihood is maximized by setting this variance component equal to 0. Whenever a zero variance component estimate occurs, the following note appears in the SAS log:
NOTE: Estimated G matrix is not positive definite.
The remaining variance component estimates are positive, and the estimate corresponding to the nested errors (MONTHC) is much larger than the other two.
A comparison of AIC and BIC for this model with those of the previous model favors the nested error model (compare Output 58.5.11 and Output 58.5.6). Strictly speaking, a likelihood ratio test cannot be carried out between the two models because one is not contained in the other; however, a cautious comparison of likelihoods can be informative.
| Fit Statistics | |
|---|---|
| -2 Res Log Likelihood | 276.9 |
| AIC (smaller is better) | 282.9 |
| AICC (smaller is better) | 283.2 |
| BIC (smaller is better) | 280.2 |
The better-fitting covariance model affects the standard errors of the fixed-effects parameter estimates more than the estimates themselves (Output 58.5.12).
| Solution for Fixed Effects | |||||
|---|---|---|---|---|---|
| Effect | Estimate | Standard Error | DF | t Value | Pr > |t| |
| Intercept | 102.56 | 0.7287 | 2 | 140.74 | <.0001 |
| Month | -0.5003 | 0.1259 | 2 | -3.97 | 0.0579 |
The random-effects solution provides the empirical best linear unbiased predictions (EBLUPs) for the realizations of the random intercept, slope, and nested errors (Output 58.5.13). You can use these values to compare batches and months.
| Solution for Random Effects | |||||||
|---|---|---|---|---|---|---|---|
| Effect | Batch | Monthc | Estimate | Std Err Pred | DF | t Value | Pr > |t| |
| Intercept | 1 | 0 | . | . | . | . | |
| Month | 1 | -0.00028 | 0.09268 | 66 | -0.00 | 0.9976 | |
| Monthc | 1 | 0 | 0.2191 | 0.7896 | 66 | 0.28 | 0.7823 |
| Monthc | 1 | 1 | -2.5690 | 0.7571 | 66 | -3.39 | 0.0012 |
| Monthc | 1 | 3 | -2.3067 | 0.6865 | 66 | -3.36 | 0.0013 |
| Monthc | 1 | 6 | 1.8726 | 0.7328 | 66 | 2.56 | 0.0129 |
| Monthc | 1 | 9 | -1.2350 | 0.9300 | 66 | -1.33 | 0.1888 |
| Monthc | 1 | 12 | 0.7736 | 1.1992 | 66 | 0.65 | 0.5211 |
| Intercept | 2 | 0 | . | . | . | . | |
| Month | 2 | -0.07571 | 0.09268 | 66 | -0.82 | 0.4169 | |
| Monthc | 2 | 0 | -0.00621 | 0.7896 | 66 | -0.01 | 0.9938 |
| Monthc | 2 | 1 | -2.2126 | 0.7571 | 66 | -2.92 | 0.0048 |
| Monthc | 2 | 3 | 3.1063 | 0.6865 | 66 | 4.53 | <.0001 |
| Monthc | 2 | 6 | 2.0649 | 0.7328 | 66 | 2.82 | 0.0064 |
| Monthc | 2 | 9 | -1.4450 | 0.9300 | 66 | -1.55 | 0.1250 |
| Monthc | 2 | 12 | -2.4405 | 1.1992 | 66 | -2.04 | 0.0459 |
| Intercept | 3 | 0 | . | . | . | . | |
| Month | 3 | 0.07600 | 0.09268 | 66 | 0.82 | 0.4152 | |
| Monthc | 3 | 0 | 1.9574 | 0.7896 | 66 | 2.48 | 0.0157 |
| Monthc | 3 | 1 | -0.8850 | 0.7571 | 66 | -1.17 | 0.2466 |
| Monthc | 3 | 3 | 0.3006 | 0.6865 | 66 | 0.44 | 0.6629 |
| Monthc | 3 | 6 | 0.7972 | 0.7328 | 66 | 1.09 | 0.2806 |
| Monthc | 3 | 9 | 2.0059 | 0.9300 | 66 | 2.16 | 0.0347 |
| Monthc | 3 | 12 | 0.002293 | 1.1992 | 66 | 0.00 | 0.9985 |
| Type 3 Tests of Fixed Effects | ||||
|---|---|---|---|---|
| Effect | Num DF | Den DF | F Value | Pr > F |
| Month | 1 | 2 | 15.78 | 0.0579 |
The test of Month is similar to that from the previous model, although it is no longer significant at the 5% level (Output 58.5.14).
