The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD Statement ASSESS Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement DEVIANCE Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement FWDLINK Statement INVLINK Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements REPEATED Statement SLICE Statement STORE Statement STRATA Statement VARIANCE Statement WEIGHT Statement ZEROMODEL Statement
PROC GENMOD Statement ASSESS Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement DEVIANCE Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement FWDLINK Statement INVLINK Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements REPEATED Statement SLICE Statement STORE Statement STRATA Statement VARIANCE Statement WEIGHT Statement ZEROMODEL Statement -
Details
 Generalized Linear Models Theory Specification of Effects Parameterization Used in PROC GENMOD Type 1 Analysis Type 3 Analysis Confidence Intervals for Parameters F Statistics Lagrange Multiplier Statistics Predicted Values of the Mean Residuals Multinomial Models Zero-Inflated Models Generalized Estimating Equations Assessment of Models Based on Aggregates of Residuals Case Deletion Diagnostic Statistics Bayesian Analysis Exact Logistic and Exact Poisson Regression Missing Values Displayed Output for Classical Analysis Displayed Output for Bayesian Analysis Displayed Output for Exact Analysis ODS Table Names ODS Graphics
Generalized Linear Models Theory Specification of Effects Parameterization Used in PROC GENMOD Type 1 Analysis Type 3 Analysis Confidence Intervals for Parameters F Statistics Lagrange Multiplier Statistics Predicted Values of the Mean Residuals Multinomial Models Zero-Inflated Models Generalized Estimating Equations Assessment of Models Based on Aggregates of Residuals Case Deletion Diagnostic Statistics Bayesian Analysis Exact Logistic and Exact Poisson Regression Missing Values Displayed Output for Classical Analysis Displayed Output for Bayesian Analysis Displayed Output for Exact Analysis ODS Table Names ODS Graphics -
Examples
 Logistic Regression Normal Regression, Log Link Gamma Distribution Applied to Life Data Ordinal Model for Multinomial Data GEE for Binary Data with Logit Link Function Log Odds Ratios and the ALR Algorithm Log-Linear Model for Count Data Model Assessment of Multiple Regression Using Aggregates of Residuals Assessment of a Marginal Model for Dependent Data Bayesian Analysis of a Poisson Regression Model Exact Poisson Regression
Logistic Regression Normal Regression, Log Link Gamma Distribution Applied to Life Data Ordinal Model for Multinomial Data GEE for Binary Data with Logit Link Function Log Odds Ratios and the ALR Algorithm Log-Linear Model for Count Data Model Assessment of Multiple Regression Using Aggregates of Residuals Assessment of a Marginal Model for Dependent Data Bayesian Analysis of a Poisson Regression Model Exact Poisson Regression - References
Example 39.11 Exact Poisson Regression
The following data, taken from Cox and Snell (1989, pp. 10–11), consists of the number, Notready, of ingots that are not ready for rolling, out of Total tested, for several combinations of heating time and soaking time:
data ingots; input Heat Soak Notready Total @@; lnTotal= log(Total); datalines; 7 1.0 0 10 14 1.0 0 31 27 1.0 1 56 51 1.0 3 13 7 1.7 0 17 14 1.7 0 43 27 1.7 4 44 51 1.7 0 1 7 2.2 0 7 14 2.2 2 33 27 2.2 0 21 51 2.2 0 1 7 2.8 0 12 14 2.8 0 31 27 2.8 1 22 51 4.0 0 1 7 4.0 0 9 14 4.0 0 19 27 4.0 1 16 ;
The following invocation of PROC GENMOD fits an asymptotic (unconditional) Poisson regression model to the data. The variable Notready is specified as the response variable, and the continuous predictors Heat and Soak are defined in the CLASS statement as categorical predictors that use reference coding. Specifying the offset variable as lnTotal enables you to model the ratio Notready/Total.
proc genmod data=ingots; class Heat Soak / param=ref; model Notready=Heat Soak / offset=lnTotal dist=poisson link=log; exact Heat Soak / joint estimate; exactoptions statustime=10; run;
The EXACT statement is specified to additionally fit an exact conditional Poisson regression model. Specifying the lnTotal offset variable models the ratio Notready/Total; in this case, the Total variable contains the largest possible response value for each observation. The JOINT option produces a joint test for the significance of the covariates, along with the usual marginal tests. The ESTIMATE option produces exact parameter estimates for the covariates. The STATUSTIME=10 option is specified in the EXACTOPTIONS statement for monitoring the progress of the results; this example can take several minutes to complete due to the JOINT option. If you run out of memory, see the SAS Companion for your system for information about how to increase the available memory.
The "Criteria For Assessing Goodness Of Fit" table is displayed in Output 39.11.1. Comparing the deviance of 10.9363 with its asymptotic chi-square with 11 degrees of freedom distribution, you find that the 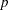 -value is 0.084. This indicates that the specified model fits the data reasonably well.
-value is 0.084. This indicates that the specified model fits the data reasonably well.
| Criteria For Assessing Goodness Of Fit | |||
|---|---|---|---|
| Criterion | DF | Value | Value/DF |
| Deviance | 11 | 10.9363 | 0.9942 |
| Scaled Deviance | 11 | 10.9363 | 0.9942 |
| Pearson Chi-Square | 11 | 9.3722 | 0.8520 |
| Scaled Pearson X2 | 11 | 9.3722 | 0.8520 |
| Log Likelihood | -7.2408 | ||
| Full Log Likelihood | -12.9038 | ||
| AIC (smaller is better) | 41.8076 | ||
| AICC (smaller is better) | 56.2076 | ||
| BIC (smaller is better) | 49.3631 | ||
| Analysis Of Maximum Likelihood Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | ||
| Intercept | 1 | -1.5700 | 1.1657 | -3.8548 | 0.7147 | 1.81 | 0.1780 | |
| Heat | 7 | 1 | -27.6129 | 264324.6 | -518094 | 518039.0 | 0.00 | 0.9999 |
| Heat | 14 | 1 | -3.0107 | 1.0025 | -4.9756 | -1.0458 | 9.02 | 0.0027 |
| Heat | 27 | 1 | -1.7180 | 0.7691 | -3.2253 | -0.2106 | 4.99 | 0.0255 |
| Soak | 1 | 1 | -0.2454 | 1.1455 | -2.4906 | 1.9998 | 0.05 | 0.8304 |
| Soak | 1.7 | 1 | 0.5572 | 1.1217 | -1.6412 | 2.7557 | 0.25 | 0.6193 |
| Soak | 2.2 | 1 | 0.4079 | 1.2260 | -1.9951 | 2.8109 | 0.11 | 0.7394 |
| Soak | 2.8 | 1 | -0.1301 | 1.4234 | -2.9199 | 2.6597 | 0.01 | 0.9272 |
| Scale | 0 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | |||
| Note: | The scale parameter was held fixed. |
Following the output from the asymptotic analysis, the exact conditional Poisson regression results are displayed, as shown in Output 39.11.3.
| Conditional Exact Tests | ||||
|---|---|---|---|---|
| Effect | Test | Statistic | p-Value | |
| Exact | Mid | |||
| Joint | Score | 18.3665 | 0.0137 | 0.0137 |
| Probability | 1.294E-6 | 0.0471 | 0.0471 | |
| Heat | Score | 15.8259 | 0.0023 | 0.0022 |
| Probability | 0.000175 | 0.0063 | 0.0062 | |
| Soak | Score | 1.4612 | 0.8683 | 0.8646 |
| Probability | 0.00735 | 0.8176 | 0.8139 | |
The Joint test in the "Conditional Exact Tests" table in Output 39.11.3 is produced by specifying the JOINT option in the EXACT statement. The 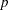 -values for this test indicate that the parameters for Heat and Soak are jointly significant as explanatory effects in the model. If the Heat variable is the only explanatory variable in your model, then the rows of this table labeled as "Heat" show the joint significance of all the Heat effect parameters in that reduced model. In this case, a model that contains only the Heat parameters still explains a significant amount of the variability; however, you can see that a model that contains only the Soak parameters would not be significant.
-values for this test indicate that the parameters for Heat and Soak are jointly significant as explanatory effects in the model. If the Heat variable is the only explanatory variable in your model, then the rows of this table labeled as "Heat" show the joint significance of all the Heat effect parameters in that reduced model. In this case, a model that contains only the Heat parameters still explains a significant amount of the variability; however, you can see that a model that contains only the Soak parameters would not be significant.
The "Exact Parameter Estimates" table in Output 39.11.4 displays parameter estimates and tests of significance for the levels of the CLASS variables. Again, the Heat=7 parameter has some difficulties; however, in the exact analysis, a median unbiased estimate is computed for the parameter instead of a maximum likelihood estimate. The confidence limits show that the Heat variable contains some explanatory power, while the categorical Soak variable is insignificant and can be dropped from the model.
| Exact Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | Estimate | Standard Error | 95% Confidence Limits | Two-sided p-Value | |||
| Heat | 7 | -2.7552 | * | . | -Infinity | -0.7864 | 0.0199 |
| Heat | 14 | -3.0255 | 1.0128 | -5.7450 | -0.6194 | 0.0113 | |
| Heat | 27 | -1.7846 | 0.8065 | -3.6779 | 0.2260 | 0.0844 | |
| Soak | 1 | -0.3231 | 1.1717 | -2.8673 | 3.6754 | 1.0000 | |
| Soak | 1.7 | 0.5375 | 1.1284 | -1.8056 | 4.4588 | 1.0000 | |
| Soak | 2.2 | 0.4035 | 1.2347 | -2.5785 | 4.5054 | 1.0000 | |
| Soak | 2.8 | -0.1661 | 1.4214 | -4.5490 | 4.2168 | 1.0000 | |
| Note: | * indicates a median unbiased estimate. |
Note: If you want to make predictions from the exact results, you can obtain an estimate for the intercept parameter by specifying the INTERCEPT keyword in the EXACT statement. You should also remove the JOINT option to reduce the amount of time and memory consumed.