The GENMOD Procedure
-
Overview
-
Getting Started
-
Syntax
PROC GENMOD Statement ASSESS Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement DEVIANCE Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement FWDLINK Statement INVLINK Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements REPEATED Statement SLICE Statement STORE Statement STRATA Statement VARIANCE Statement WEIGHT Statement ZEROMODEL Statement
-
Details
Generalized Linear Models Theory Specification of Effects Parameterization Used in PROC GENMOD Type 1 Analysis Type 3 Analysis Confidence Intervals for Parameters F Statistics Lagrange Multiplier Statistics Predicted Values of the Mean Residuals Multinomial Models Zero-Inflated Models Generalized Estimating Equations Assessment of Models Based on Aggregates of Residuals Case Deletion Diagnostic Statistics Bayesian Analysis Exact Logistic and Exact Poisson Regression Missing Values Displayed Output for Classical Analysis Displayed Output for Bayesian Analysis Displayed Output for Exact Analysis ODS Table Names ODS Graphics
-
Examples
Logistic Regression Normal Regression, Log Link Gamma Distribution Applied to Life Data Ordinal Model for Multinomial Data GEE for Binary Data with Logit Link Function Log Odds Ratios and the ALR Algorithm Log-Linear Model for Count Data Model Assessment of Multiple Regression Using Aggregates of Residuals Assessment of a Marginal Model for Dependent Data Bayesian Analysis of a Poisson Regression Model Exact Poisson Regression
- References
| F Statistics |
Suppose that 
is the deviance resulting from fitting a generalized linear model and that 
is the deviance from fitting a submodel. Then, under appropriate regularity conditions, the asymptotic distribution of 
is chi-square with 
degrees of freedom, where is the difference in the number of parameters between the two models and 
is the dispersion parameter. If is unknown, and 
is an estimate of based on the deviance or Pearson’s chi-square divided by degrees of freedom, then, under regularity conditions, 
has an asymptotic chi-square distribution with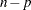 
degrees of freedom. Here, 
is the number of observations and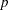 
is the number of parameters in the model that is used to estimate . Thus, the asymptotic distribution of
 |
is the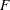 
distribution with and 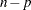degrees of freedom, assuming that and are approximately independent.
This 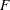statistic is computed for the Type 1 analysis, Type 3 analysis, and hypothesis tests specified in CONTRAST statements when the dispersion parameter is estimated by either the deviance or Pearson’s chi-square divided by degrees of freedom, as specified by the DSCALE or PSCALE option in the MODEL statement. In the case of a Type 1 analysis, model 0 is the higher-order model obtained by including one additional effect in model 1. For a Type 3 analysis and hypothesis tests, model 0 is the full specified model and model 1 is the submodel obtained from constraining the Type III contrast or the user-specified contrast to be 0.