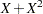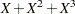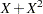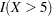The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD Statement ASSESS Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement DEVIANCE Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement FWDLINK Statement INVLINK Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements REPEATED Statement SLICE Statement STORE Statement STRATA Statement VARIANCE Statement WEIGHT Statement ZEROMODEL Statement
PROC GENMOD Statement ASSESS Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement DEVIANCE Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement FWDLINK Statement INVLINK Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements REPEATED Statement SLICE Statement STORE Statement STRATA Statement VARIANCE Statement WEIGHT Statement ZEROMODEL Statement -
Details
 Generalized Linear Models Theory Specification of Effects Parameterization Used in PROC GENMOD Type 1 Analysis Type 3 Analysis Confidence Intervals for Parameters F Statistics Lagrange Multiplier Statistics Predicted Values of the Mean Residuals Multinomial Models Zero-Inflated Models Generalized Estimating Equations Assessment of Models Based on Aggregates of Residuals Case Deletion Diagnostic Statistics Bayesian Analysis Exact Logistic and Exact Poisson Regression Missing Values Displayed Output for Classical Analysis Displayed Output for Bayesian Analysis Displayed Output for Exact Analysis ODS Table Names ODS Graphics
Generalized Linear Models Theory Specification of Effects Parameterization Used in PROC GENMOD Type 1 Analysis Type 3 Analysis Confidence Intervals for Parameters F Statistics Lagrange Multiplier Statistics Predicted Values of the Mean Residuals Multinomial Models Zero-Inflated Models Generalized Estimating Equations Assessment of Models Based on Aggregates of Residuals Case Deletion Diagnostic Statistics Bayesian Analysis Exact Logistic and Exact Poisson Regression Missing Values Displayed Output for Classical Analysis Displayed Output for Bayesian Analysis Displayed Output for Exact Analysis ODS Table Names ODS Graphics -
Examples
 Logistic Regression Normal Regression, Log Link Gamma Distribution Applied to Life Data Ordinal Model for Multinomial Data GEE for Binary Data with Logit Link Function Log Odds Ratios and the ALR Algorithm Log-Linear Model for Count Data Model Assessment of Multiple Regression Using Aggregates of Residuals Assessment of a Marginal Model for Dependent Data Bayesian Analysis of a Poisson Regression Model Exact Poisson Regression
Logistic Regression Normal Regression, Log Link Gamma Distribution Applied to Life Data Ordinal Model for Multinomial Data GEE for Binary Data with Logit Link Function Log Odds Ratios and the ALR Algorithm Log-Linear Model for Count Data Model Assessment of Multiple Regression Using Aggregates of Residuals Assessment of a Marginal Model for Dependent Data Bayesian Analysis of a Poisson Regression Model Exact Poisson Regression - References
Example 39.8 Model Assessment of Multiple Regression Using Aggregates of Residuals
This example illustrates the use of cumulative residuals to assess the adequacy of a normal linear regression model. Neter et al. (1996, Section 8.2) describe a study of 54 patients undergoing a certain kind of liver operation in a surgical unit. The data consist of the survival time and certain covariates. After a model selection procedure, they arrived at the following model:
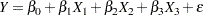 |
where 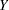 is the logarithm (base 10) of the survival time;
is the logarithm (base 10) of the survival time; 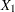 ,
, 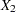 ,
, 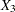 are blood-clotting score, prognostic index, and enzyme function, respectively; and
are blood-clotting score, prognostic index, and enzyme function, respectively; and  is a normal error term. A listing of the SAS data set containing the data is shown in Output 39.8.1. The variables Y, X1, X2, and X3 correspond to
is a normal error term. A listing of the SAS data set containing the data is shown in Output 39.8.1. The variables Y, X1, X2, and X3 correspond to 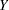 ,
, 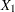 ,
, 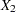 , and
, and 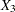 , and LogX1 is log(
, and LogX1 is log(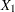 ). The PROC GENMOD fit of the model is shown in Output 39.8.2. The analysis first focuses on the adequacy of the functional form of
). The PROC GENMOD fit of the model is shown in Output 39.8.2. The analysis first focuses on the adequacy of the functional form of 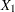 , blood-clotting score.
, blood-clotting score.
| Obs | Y | X1 | X2 | X3 | LogX1 |
|---|---|---|---|---|---|
| 1 | 2.3010 | 6.7 | 62 | 81 | 0.82607 |
| 2 | 2.0043 | 5.1 | 59 | 66 | 0.70757 |
| 3 | 2.3096 | 7.4 | 57 | 83 | 0.86923 |
| 4 | 2.0043 | 6.5 | 73 | 41 | 0.81291 |
| 5 | 2.7067 | 7.8 | 65 | 115 | 0.89209 |
| 6 | 1.9031 | 5.8 | 38 | 72 | 0.76343 |
| 7 | 1.9031 | 5.7 | 46 | 63 | 0.75587 |
| 8 | 2.1038 | 3.7 | 68 | 81 | 0.56820 |
| 9 | 2.3054 | 6.0 | 67 | 93 | 0.77815 |
| 10 | 2.3075 | 3.7 | 76 | 94 | 0.56820 |
| 11 | 2.5172 | 6.3 | 84 | 83 | 0.79934 |
| 12 | 1.8129 | 6.7 | 51 | 43 | 0.82607 |
| 13 | 2.9191 | 5.8 | 96 | 114 | 0.76343 |
| 14 | 2.5185 | 5.8 | 83 | 88 | 0.76343 |
| 15 | 2.2253 | 7.7 | 62 | 67 | 0.88649 |
| 16 | 2.3365 | 7.4 | 74 | 68 | 0.86923 |
| 17 | 1.9395 | 6.0 | 85 | 28 | 0.77815 |
| 18 | 1.5315 | 3.7 | 51 | 41 | 0.56820 |
| 19 | 2.3324 | 7.3 | 68 | 74 | 0.86332 |
| 20 | 2.2355 | 5.6 | 57 | 87 | 0.74819 |
| 21 | 2.0374 | 5.2 | 52 | 76 | 0.71600 |
| 22 | 2.1335 | 3.4 | 83 | 53 | 0.53148 |
| 23 | 1.8451 | 6.7 | 26 | 68 | 0.82607 |
| 24 | 2.3424 | 5.8 | 67 | 86 | 0.76343 |
| 25 | 2.4409 | 6.3 | 59 | 100 | 0.79934 |
| 26 | 2.1584 | 5.8 | 61 | 73 | 0.76343 |
| 27 | 2.2577 | 5.2 | 52 | 86 | 0.71600 |
| 28 | 2.7589 | 11.2 | 76 | 90 | 1.04922 |
| 29 | 1.8573 | 5.2 | 54 | 56 | 0.71600 |
| 30 | 2.2504 | 5.8 | 76 | 59 | 0.76343 |
| 31 | 1.8513 | 3.2 | 64 | 65 | 0.50515 |
| 32 | 1.7634 | 8.7 | 45 | 23 | 0.93952 |
| 33 | 2.0645 | 5.0 | 59 | 73 | 0.69897 |
| 34 | 2.4698 | 5.8 | 72 | 93 | 0.76343 |
| 35 | 2.0607 | 5.4 | 58 | 70 | 0.73239 |
| 36 | 2.2648 | 5.3 | 51 | 99 | 0.72428 |
| 37 | 2.0719 | 2.6 | 74 | 86 | 0.41497 |
| 38 | 2.0792 | 4.3 | 8 | 119 | 0.63347 |
| 39 | 2.1790 | 4.8 | 61 | 76 | 0.68124 |
| 40 | 2.1703 | 5.4 | 52 | 88 | 0.73239 |
| 41 | 1.9777 | 5.2 | 49 | 72 | 0.71600 |
| 42 | 1.8751 | 3.6 | 28 | 99 | 0.55630 |
| 43 | 2.6840 | 8.8 | 86 | 88 | 0.94448 |
| 44 | 2.1847 | 6.5 | 56 | 77 | 0.81291 |
| 45 | 2.2810 | 3.4 | 77 | 93 | 0.53148 |
| 46 | 2.0899 | 6.5 | 40 | 84 | 0.81291 |
| 47 | 2.4928 | 4.5 | 73 | 106 | 0.65321 |
| 48 | 2.5999 | 4.8 | 86 | 101 | 0.68124 |
| 49 | 2.1987 | 5.1 | 67 | 77 | 0.70757 |
| 50 | 2.4914 | 3.9 | 82 | 103 | 0.59106 |
| 51 | 2.0934 | 6.6 | 77 | 46 | 0.81954 |
| 52 | 2.0969 | 6.4 | 85 | 40 | 0.80618 |
| 53 | 2.2967 | 6.4 | 59 | 85 | 0.80618 |
| 54 | 2.4955 | 8.8 | 78 | 72 | 0.94448 |
In order to assess the adequacy of the fitted multiple regression model, the ASSESS statement in the following SAS statements is used to create the plots of cumulative residuals against X1 shown in Output 39.8.3 and Output 39.8.4 and the summary table in Output 39.8.5:
ods graphics on;
proc genmod data=Surg;
model Y = X1 X2 X3 / scale=Pearson;
assess var=(X1) / resample=10000
seed=603708000
crpanel ;
run;
| Analysis Of Maximum Likelihood Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | |
| Intercept | 1 | 0.4836 | 0.0426 | 0.4001 | 0.5672 | 128.71 | <.0001 |
| X1 | 1 | 0.0692 | 0.0041 | 0.0612 | 0.0772 | 288.17 | <.0001 |
| X2 | 1 | 0.0093 | 0.0004 | 0.0085 | 0.0100 | 590.45 | <.0001 |
| X3 | 1 | 0.0095 | 0.0003 | 0.0089 | 0.0101 | 966.07 | <.0001 |
| Scale | 0 | 0.0469 | 0.0000 | 0.0469 | 0.0469 | ||
| Note: | The scale parameter was estimated by the square root of Pearson's Chi-Square/DOF. |
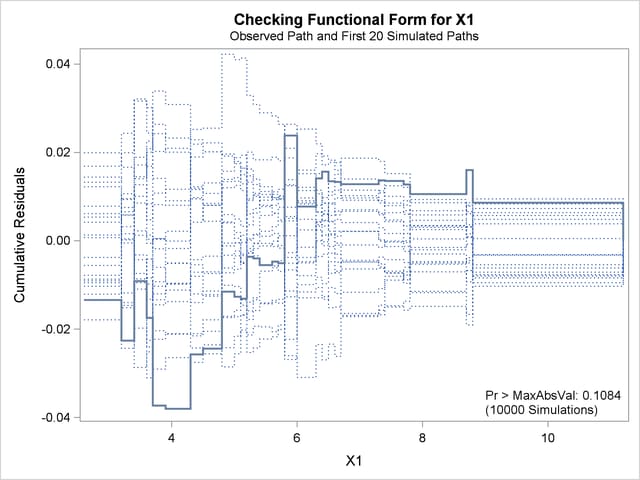
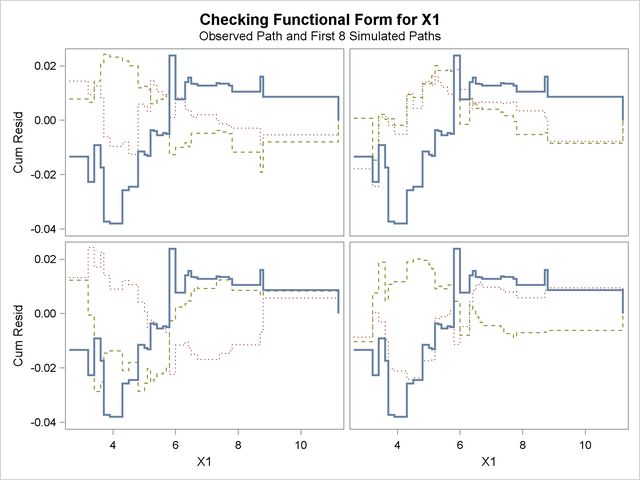
See Lin, Wei, and Ying (2002) for details about model assessment that uses cumulative residual plots. The RESAMPLE= keyword specifies that a 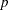 -value be computed based on a sample of 10,000 simulated residual paths. A random number seed is specified by the SEED= keyword for reproducibility. If you do not specify the seed, one is derived from the time of day. The keyword CRPANEL specifies that the panel of four cumulative residual plots shown in Output 39.8.4 be created, each with two simulated paths. The single residual plot with 20 simulated paths in Output 39.8.3 is created by default.
-value be computed based on a sample of 10,000 simulated residual paths. A random number seed is specified by the SEED= keyword for reproducibility. If you do not specify the seed, one is derived from the time of day. The keyword CRPANEL specifies that the panel of four cumulative residual plots shown in Output 39.8.4 be created, each with two simulated paths. The single residual plot with 20 simulated paths in Output 39.8.3 is created by default.
To request these graphs, ODS Graphics must be enabled and you must specify the ASSESS statement. For general information about ODS Graphics, see Chapter 21, Statistical Graphics Using ODS. For specific information about the graphics available in the GENMOD procedure, see the section ODS Graphics.
| Assessment Summary | ||||
|---|---|---|---|---|
| Assessment Variable |
Maximum Absolute Value |
Replications | Seed | Pr > MaxAbsVal |
| X1 | 0.0380 | 10000 | 603708000 | 0.1084 |
The 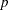 -value of 0.1084 reported on Output 39.8.3 and Output 39.8.5 suggests that a more adequate model might be possible. The observed cumulative residuals in Output 39.8.3 and Output 39.8.4, represented by the heavy lines, seem atypical of the simulated curves, represented by the light lines, reinforcing the conclusion that a more appropriate functional form for X1 is possible.
-value of 0.1084 reported on Output 39.8.3 and Output 39.8.5 suggests that a more adequate model might be possible. The observed cumulative residuals in Output 39.8.3 and Output 39.8.4, represented by the heavy lines, seem atypical of the simulated curves, represented by the light lines, reinforcing the conclusion that a more appropriate functional form for X1 is possible.
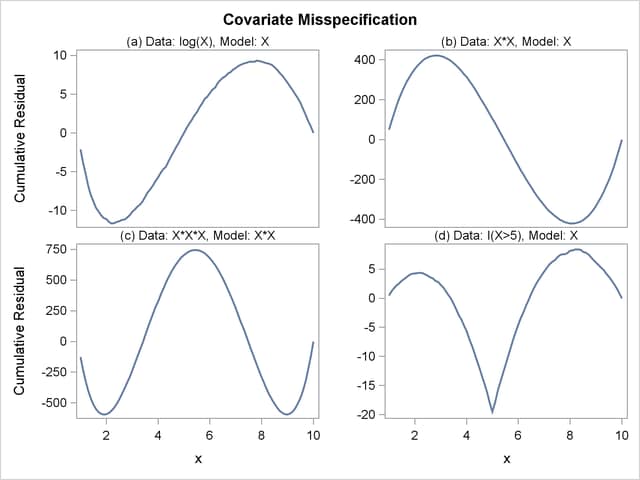
The cumulative residual plots in Output 39.8.6 provide guidance in determining a more appropriate functional form. The four curves were created from simple forms of model misspecification by using simulated data. The mean models of the data and the fitted model are shown in Table 39.15.
Plot |
Data E( |
Fitted Model E( |
|---|---|---|
(a) |
log( |
|
(b) |
|
|
(c) |
|
|
(d) |
|
|
The observed cumulative residual pattern in Output 39.8.3 and Output 39.8.4 most resembles the behavior of the curve in plot (a) of Output 39.8.6, indicating that log(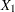 ) might be a more appropriate term in the model than
) might be a more appropriate term in the model than 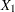 .
.
The following SAS statements fit a model with LogX1 in place of X1 and request a model assessment:
proc genmod data=Surg;
model Y = LogX1 X2 X3 / scale=Pearson;
assess var=(LogX1) / resample=10000
seed=603708000;
run;
ods graphics off;
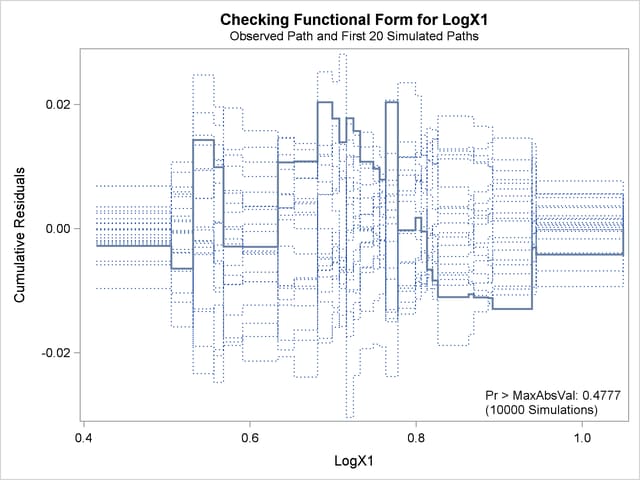
The revised model fit is shown in Output 39.8.7, the 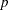 -value from the simulation is 0.4777, and the cumulative residuals plotted in Output 39.8.8 show no systematic trend. The log transformation for X1 is more appropriate. Under the revised model, the
-value from the simulation is 0.4777, and the cumulative residuals plotted in Output 39.8.8 show no systematic trend. The log transformation for X1 is more appropriate. Under the revised model, the 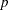 -values for testing the functional forms of X2 and X3 are 0.20 and 0.63, respectively; and the
-values for testing the functional forms of X2 and X3 are 0.20 and 0.63, respectively; and the 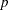 -value for testing the linearity of the model is 0.65. Thus, the revised model seems reasonable.
-value for testing the linearity of the model is 0.65. Thus, the revised model seems reasonable.
| Analysis Of Maximum Likelihood Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | |
| Intercept | 1 | 0.1844 | 0.0504 | 0.0857 | 0.2832 | 13.41 | 0.0003 |
| LogX1 | 1 | 0.9121 | 0.0491 | 0.8158 | 1.0083 | 345.05 | <.0001 |
| X2 | 1 | 0.0095 | 0.0004 | 0.0088 | 0.0102 | 728.62 | <.0001 |
| X3 | 1 | 0.0096 | 0.0003 | 0.0090 | 0.0101 | 1139.73 | <.0001 |
| Scale | 0 | 0.0434 | 0.0000 | 0.0434 | 0.0434 | ||
| Note: | The scale parameter was estimated by the square root of Pearson's Chi-Square/DOF. |
 )
)