The UNIVARIATE Procedure

PROC UNIVARIATE Statement

PROC UNIVARIATE <options> ;

The PROC UNIVARIATE statement is required to invoke the UNIVARIATE procedure. You can use the PROC UNIVARIATE statement by itself to request a variety of statistics for summarizing the data distribution of each analysis variable:

sample moments
basic measures of location and variability
confidence intervals for the mean, standard deviation, and variance
tests for location
tests for normality
trimmed and Winsorized means
robust estimates of scale
quantiles and related confidence intervals
extreme observations and extreme values
frequency counts for observations
missing values

In addition, you can use options in the PROC UNIVARIATE statement to do the following:

specify the input data set to be analyzed
specify a graphics catalog for saving traditional graphics output
specify rounding units for variable values
specify the definition used to calculate percentiles
specify the divisor used to calculate variances and standard deviations
request that plots be produced on line printers and define special printing characters used for features
suppress tables
save statistics in an output data set

The following are the options that can be used with the PROC UNIVARIATE statement:

ALL

requests all statistics and tables that the FREQ, MODES, NEXTRVAL=5, PLOT, and CIBASIC options generate. If the analysis variables are not weighted, this option also requests the statistics and tables generated by the CIPCTLDF, CIPCTLNORMAL, LOCCOUNT, NORMAL, ROBUSTSCALE, TRIMMED=.25, and WINSORIZED=.25 options. PROC UNIVARIATE also uses any values that you specify for ALPHA=, MU0=, NEXTRVAL=, CIBASIC, CIPCTLDF, CIPCTLNORMAL, TRIMMED=, or WINSORIZED= to produce the output.

ALPHA= $\alpha$

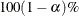specifies the level of significance $\alpha$ for $100(1-\alpha )\%$ confidence intervals. The value $\alpha$ must be between 0 and 1; the default value is 0.05, which results in 95% confidence intervals.

Note that specialized ALPHA= options are available for a number of confidence interval options. For example, you can specify CIBASIC(ALPHA=0.10) to request a table of basic confidence limits at the 90% level. The default value of these options is the value of the ALPHA= option in the PROC statement.

ANNOTATE=SAS-data-set ANNO=SAS-data-set

specifies an input data set that contains annotate variables as described in SAS/GRAPH: Reference. You can use this data set to add features to your traditional graphics. PROC UNIVARIATE adds the features in this data set to every graph that is produced in the procedure. PROC UNIVARIATE does not use the ANNOTATE= data set unless you create a traditional graph with a plot statement. The option does not apply to ODS Graphics output. Use the ANNOTATE= option in the plot statement if you want to add a feature to a specific graph produced by that statement.

CIBASIC <(<TYPE=keyword> <ALPHA= $\alpha$ >)>

requests confidence limits for the mean, standard deviation, and variance based on the assumption that the data are normally distributed. If you use the CIBASIC option, you must use the default value of VARDEF=, which is DF.

TYPE=keyword: specifies the type of confidence limit, where keyword is LOWER, UPPER, or TWOSIDED. The default value is TWOSIDED.
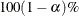ALPHA= $\alpha$: specifies the level of significance $\alpha$ for $100(1-\alpha )\%$ confidence intervals. The value $\alpha$ must be between 0 and 1; the default value is 0.05, which results in 95% confidence intervals. The default value is the value of ALPHA= given in the PROC statement.

CIPCTLDF <(<TYPE=keyword> <ALPHA= $\alpha$ >)> CIQUANTDF <(<TYPE=keyword> <ALPHA= $\alpha$ >)>

requests confidence limits for quantiles based on a method that is distribution-free. In other words, no specific parametric distribution such as the normal is assumed for the data. PROC UNIVARIATE uses order statistics (ranks) to compute the confidence limits as described by Hahn and Meeker (1991). This option does not apply if you use a WEIGHT statement.

TYPE=keyword: specifies the type of confidence limit, where keyword is LOWER, UPPER, SYMMETRIC, or ASYMMETRIC. The default value is SYMMETRIC.
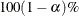ALPHA= $\alpha$: specifies the level of significance $\alpha$ for $100(1-\alpha )\%$ confidence intervals. The value $\alpha$ must be between 0 and 1; the default value is 0.05, which results in 95% confidence intervals. The default value is the value of ALPHA= given in the PROC statement.

CIPCTLNORMAL <(<TYPE=keyword> <ALPHA= $\alpha$ >)> CIQUANTNORMAL <(<TYPE=keyword> <ALPHA= $\alpha$ >)>

requests confidence limits for quantiles based on the assumption that the data are normally distributed. The computational method is described in Section 4.4.1 of Hahn and Meeker (1991) and uses the noncentral distribution as given by Odeh and Owen (1980). This option does not apply if you use a WEIGHT statement

TYPE=keyword: specifies the type of confidence limit, where keyword is LOWER, UPPER, or TWOSIDED. The default is TWOSIDED.
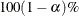ALPHA= $\alpha$: specifies the level of significance $\alpha$ for $100(1-\alpha )\%$ confidence intervals. The value $\alpha$ must be between 0 and 1; the default value is 0.05, which results in 95% confidence intervals. The default value is the value of ALPHA= given in the PROC statement.

DATA=SAS-data-set

specifies the input SAS data set to be analyzed. If the DATA= option is omitted, the procedure uses the most recently created SAS data set.

EXCLNPWGT EXCLNPWGTS

excludes observations with nonpositive weight values (zero or negative) from the analysis. By default, PROC UNIVARIATE counts observations with negative or zero weights in the total number of observations. This option applies only when you use a WEIGHT statement.

FREQ

requests a frequency table that consists of the variable values, frequencies, cell percentages, and cumulative percentages.

If you specify the WEIGHT statement, PROC UNIVARIATE includes the weighted count in the table and uses this value to compute the percentages.

GOUT=graphics-catalog

specifies the SAS catalog that PROC UNIVARIATE uses to save traditional graphics output. If you omit the libref in the name of the graphics-catalog, PROC UNIVARIATE looks for the catalog in the temporary library called WORK and creates the catalog if it does not exist. The option does not apply to ODS Graphics output.

IDOUT

includes ID variables in the output data set created by an OUTPUT statement. The value of an ID variable in the output data set is its first value from the input data set or BY group. By default, ID variables are not included in OUTPUT statement data sets.

LOCCOUNT

requests a table that shows the number of observations greater than, not equal to, and less than the value of MU0=. PROC UNIVARIATE uses these values to construct the sign test and the signed rank test. This option does not apply if you use a WEIGHT statement.

MODES|MODE

requests a table of all possible modes. By default, when the data contain multiple modes, PROC UNIVARIATE displays the lowest mode in the table of basic statistical measures. When all the values are unique, PROC UNIVARIATE does not produce a table of modes.

MU0=values LOCATION=values

specifies the value of the mean or location parameter ( 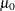$\mu _0$ ) in the null hypothesis for tests of location summarized in the table labeled “Tests for Location: Mu0=value.” If you specify one value, PROC UNIVARIATE tests the same null hypothesis for all analysis variables. If you specify multiple values, a VAR statement is required, and PROC UNIVARIATE tests a different null hypothesis for each analysis variable, matching variables and location values by their order in the two lists. The default value is 0.

The following statement tests the hypothesis 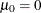$\mu _0=0$ for the first variable and the hypothesis $\mu _0=0.5$ for the second variable.

proc univariate mu0=0 0.5;

NEXTROBS=n

specifies the number of extreme observations that PROC UNIVARIATE lists in the table of extreme observations. The table lists the lowest observations and the highest observations. The default value is 5. You can specify NEXTROBS=0 to suppress the table of extreme observations.

NEXTRVAL=n

specifies the number of extreme values that PROC UNIVARIATE lists in the table of extreme values. The table lists the lowest unique values and the highest unique values. By default, and no table is displayed.

NOBYPLOT

suppresses side-by-side line printer box plots that are created by default when you use the BY statement and either the ALL option or the PLOT option in the PROC statement.

NOPRINT

suppresses all the tables of descriptive statistics that the PROC UNIVARIATE statement creates. NOPRINT does not suppress the tables that the HISTOGRAM statement creates. You can use the NOPRINT option in the HISTOGRAM statement to suppress the creation of its tables. Use NOPRINT when you want to create an OUT= or OUTTABLE= output data set only.

NORMAL NORMALTEST

requests tests for normality that include a series of goodness-of-fit tests based on the empirical distribution function. The table provides test statistics and 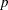-values for the Shapiro-Wilk test (provided the sample size is less than or equal to 2000), the Kolmogorov-Smirnov test, the Anderson-Darling test, and the Cramér–von Mises test. This option does not apply if you use a WEIGHT statement.

NOTABCONTENTS

suppresses the table of contents entries for tables of summary statistics produced by the PROC UNIVARIATE statement.

NOVARCONTENTS

suppresses grouping entries associated with analysis variables in the table of contents. By default, the table of contents lists results associated with an analysis variable in a group with the variable name.

OUTTABLE=SAS-data-set

creates an output data set that contains univariate statistics arranged in tabular form, with one observation per analysis variable. See the section OUTTABLE= Output Data Set for details.

PCTLDEF=value DEF=value

specifies the definition that PROC UNIVARIATE uses to calculate quantiles. The default value is 5. Values can be 1, 2, 3, 4, or 5. You cannot use PCTLDEF= when you compute weighted quantiles. See the section Calculating Percentiles for details on quantile definitions.

PLOTS | PLOT< ( <plot-options> <SSPLOT(plot-options)> ) >

produces a panel of plots for each analysis variable. If ODS Graphics is enabled, the panel contains a horizontal histogram, a box plot, and a normal probability plot. Otherwise, the procedure produces a stem-and-leaf plot (or a horizontal bar chart), a box plot, and a normal probability plot by using line printer output. If you specify a BY statement, side-by-side box plots of the data from the BY groups are displayed following the univariate output for the last BY group.

You can specify the following plot options to produce titles and footnotes for the plots when ODS Graphics is enabled. Plot options that are specified within the SSPLOT suboption apply to the side-by-side box plots of BY-group data.

ODSFOOTNOTE=FOOTNOTE | FOOTNOTE1 | 'string'

adds a footnote to ODS Graphics output. If you specify the FOOTNOTE (or FOOTNOTE1) keyword, the value of the SAS FOOTNOTE statement is used as the graph footnote. If you specify a quoted string, that is used as the footnote. The quoted string can contain either of the following escaped characters, which are replaced with the appropriate values from the analysis:

$\backslash$ n: is replaced by the analysis variable name.
$\backslash$ l: is replaced by the analysis variable label (or name if the analysis variable has no label).

ODSFOOTNOTE2=FOOTNOTE2 | 'string'

adds a secondary footnote to ODS Graphics output. If you specify the FOOTNOTE2 keyword, the value of the SAS FOOTNOTE2 statement is used as the secondary graph footnote. If you specify a quoted string, that is used as the secondary footnote. The quoted string can contain any of the following escaped characters, which are replaced with the appropriate values from the analysis:

$\backslash$ n: is replaced by the analysis variable name.
$\backslash$ l: is replaced by the analysis variable label (or name if the analysis variable has no label).

specifies a title for ODS Graphics output.

TITLE (or TITLE1): uses the value of SAS TITLE statement as the graph title.
NONE: suppresses all titles from the graph.
DEFAULT: uses the default ODS Graphics title (a descriptive title that consists of the plot type and the analysis variable name).
LABELFMT: uses the default ODS Graphics title with the variable label instead of the variable name.

If you specify a quoted string, that is used as the graph title. The quoted string can contain the following escaped characters, which are replaced with the appropriate values from the analysis:

$\backslash$ n: is replaced by the analysis variable name.
$\backslash$ l: is replaced by the analysis variable label (or name if the analysis variable has no label).

ODSTITLE2=TITLE2 | 'string'

specifies a secondary title for ODS Graphics output. If you specify the TITLE2 keyword, the value of the SAS TITLE2 statement is used as the secondary graph title. If you specify a quoted string, that is used as the secondary title. The quoted string can contain the following escaped characters, which are replaced with the appropriate values from the analysis:

$\backslash$ n: is replaced by the analysis variable name.
$\backslash$ l: is replaced by the analysis variable label (or name if the analysis variable has no label).

Note: ODSTITLE=LABELFMT and the substitution of analysis variable names and labels are not supported for plot options specified within the SSPLOT suboption.

PLOTSIZE=n

specifies the approximate number of rows used in line-printer plots requested with the PLOTS option. If is larger than the value of the SAS system option PAGESIZE=, PROC UNIVARIATE uses the value of PAGESIZE=. If is less than 8, PROC UNIVARIATE uses eight rows to draw the plots.

ROBUSTSCALE

produces a table with robust estimates of scale. The statistics include the interquartile range, Gini’s mean difference, the median absolute deviation about the median (MAD), and two statistics proposed by Rousseeuw and Croux (1993), 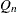, and 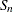. See the section Robust Estimates of Scale for details. This option does not apply if you use a WEIGHT statement.

ROUND=units

specifies the units to use to round the analysis variables prior to computing statistics. If you specify one unit, PROC UNIVARIATE uses this unit to round all analysis variables. If you specify multiple units, a VAR statement is required, and each unit rounds the values of the corresponding analysis variable. If ROUND=0, no rounding occurs. The ROUND= option reduces the number of unique variable values, thereby reducing memory requirements for the procedure. For example, to make the rounding unit 1 for the first analysis variable and 0.5 for the second analysis variable, submit the statement

proc univariate round=1 0.5;
   var Yieldstrength tenstren;
run;

When a variable value is midway between the two nearest rounded points, the value is rounded to the nearest even multiple of the roundoff value. For example, with a roundoff value of 1, the variable values of 2.5, 2.2, and 1.5 are rounded to 2; the values of 0.5, 0.2, and 0.5 are rounded to 0; and the values of 0.6, 1.2, and 1.4 are rounded to 1.

SUMMARYCONTENTS=’string’

specifies the table of contents entry used for grouping the summary statistics produced by the PROC UNIVARIATE statement. You can specify SUMMARYCONTENTS='' to suppress the grouping entry.

TRIMMED=values <(<TYPE=keyword> <ALPHA= $\alpha$ >)> TRIM=values <(<TYPE=keyword> <ALPHA= $\alpha$ >)>

requests a table of trimmed means, where value specifies the number or the proportion of observations that PROC UNIVARIATE trims. If the value is the number of trimmed observations, must be between 0 and half the number of nonmissing observations. If value is a proportion 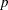between 0 and ½, the number of observations that PROC UNIVARIATE trims is the smallest integer that is greater than or equal to 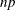, where is the number of observations. To include confidence limits for the mean and the Student’s test in the table, you must use the default value of VARDEF=, which is DF. For details concerning the computation of trimmed means, see the section Trimmed Means. The TRIMMED= option does not apply if you use a WEIGHT statement.

TYPE=keyword: specifies the type of confidence limit for the mean, where keyword is LOWER, UPPER, or TWOSIDED. The default value is TWOSIDED.
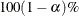ALPHA= $\alpha$: specifies the level of significance $\alpha$ for $100(1-\alpha )\%$ confidence intervals. The value $\alpha$ must be between 0 and 1; the default value is 0.05, which results in 95% confidence intervals.

VARDEF=divisor

specifies the divisor to use in the calculation of variances and standard deviation. By default, VARDEF=DF. Table 4.1 shows the possible values for divisor and associated divisors.

Table 4.1: Possible Values for VARDEF=

Value	Divisor	Formula for Divisor
DF	degrees of freedom
N	number of observations
WDF	sum of weights minus one	$(\Sigma _ i w_ i) - 1$
WEIGHT \| WGT	sum of weights	$\Sigma _ i w_ i$

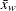The procedure computes the variance as $\frac{CSS}{\mr {divisor}}$ where is the corrected sums of squares and equals $\sum _{i=1}^ n (x_ i-\bar{x})^2$ . When you weight the analysis variables, $CSS = \sum _{i=1}^ n w_ i(x_ i - \bar{x}_ w)^2$ where $\bar{x}_ w$ is the weighted mean.

The default value is DF. To compute the standard error of the mean, confidence limits, and Student’s test, use the default value of VARDEF=.

When you use the WEIGHT statement and VARDEF=DF, the variance is an estimate of where the variance of the 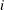th observation is $var(x_ i) = \frac{s^2}{w_ i}$ and 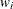is the weight for the 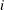th observation. This yields an estimate of the variance of an observation with unit weight.

When you use the WEIGHT statement and VARDEF=WGT, the computed variance is asymptotically (for large ) an estimate of $\frac{s^2}{\bar{w}}$ where $\bar{w}$ is the average weight. This yields an asymptotic estimate of the variance of an observation with average weight.

WINSORIZED=values <(<TYPE=keyword> <ALPHA= $\alpha$ >)> WINSOR=values <(<TYPE=keyword> <ALPHA= $\alpha$ >)>

requests of a table of Winsorized means, where value is the number or the proportion of observations that PROC UNIVARIATE uses to compute the Winsorized mean. If the value is the number of Winsorized observations, must be between 0 and half the number of nonmissing observations. If value is a proportion 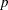between 0 and ½, the number of observations that PROC UNIVARIATE uses is equal to the smallest integer that is greater than or equal to 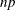, where is the number of observations. To include confidence limits for the mean and the Student test in the table, you must use the default value of VARDEF=, which is DF. For details concerning the computation of Winsorized means, see the section Winsorized Means. The WINSORIZED= option does not apply if you use a WEIGHT statement.

TYPE=keyword: specifies the type of confidence limit for the mean, where keyword is LOWER, UPPER, or TWOSIDED. The default is TWOSIDED.
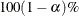ALPHA= $\alpha$: specifies the level of significance $\alpha$ for $100(1-\alpha )\%$ confidence intervals. The value $\alpha$ must be between 0 and 1; the default value is 0.05, which results in 95% confidence intervals.