The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources
Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources -
Examples
 Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Plots for Line Printer OutputAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot
Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Plots for Line Printer OutputAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot - References
Example 4.21 Fitting a Beta Curve
You can use a beta distribution to model the distribution of a variable that is known to vary between lower and upper bounds.
In this example, a manufacturing company uses a robotic arm to attach hinges on metal sheets. The attachment point should
be offset 10.1 mm from the left edge of the sheet. The actual offset varies between 10.0 and 10.5 mm due to variation in the
arm. The following statements save the offsets for 50 attachment points as the values of the variable Length in the data set Robots:
data Robots; input Length @@; label Length = 'Attachment Point Offset (in mm)'; datalines; 10.147 10.070 10.032 10.042 10.102 10.034 10.143 10.278 10.114 10.127 10.122 10.018 10.271 10.293 10.136 10.240 10.205 10.186 10.186 10.080 10.158 10.114 10.018 10.201 10.065 10.061 10.133 10.153 10.201 10.109 10.122 10.139 10.090 10.136 10.066 10.074 10.175 10.052 10.059 10.077 10.211 10.122 10.031 10.322 10.187 10.094 10.067 10.094 10.051 10.174 ;
The following statements create a histogram with a fitted beta density curve, shown in Output 4.21.1:
title 'Fitted Beta Distribution of Offsets';
ods graphics off;
ods select ParameterEstimates FitQuantiles MyHist;
proc univariate data=Robots;
histogram Length /
beta(theta=10 scale=0.5 color=red fill)
href = 10
hreflabel = 'Lower Bound'
lhref = 2
vaxis = axis1
name = 'MyHist';
axis1 label=(a=90 r=0);
inset n = 'Sample Size'
beta / pos=ne cfill=blank;
run;
The ODS SELECT statement restricts the output to the “ParameterEstimates” and “FitQuantiles” tables; see the section ODS Table Names. The BETA primary option requests a fitted beta distribution. The THETA= secondary option specifies the lower threshold. The SCALE= secondary option specifies the range between the lower threshold and the upper threshold. Note that the default THETA= and SCALE= values are zero and one, respectively.
Output 4.21.1: Superimposing a Histogram with a Fitted Beta Curve
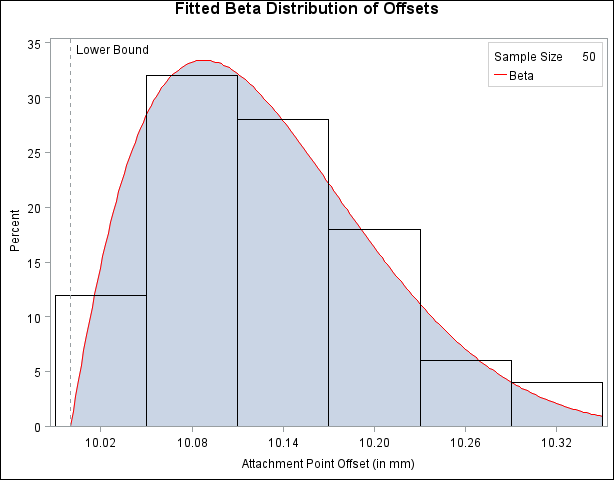
The FILL secondary option specifies that the area under the curve is to be filled with the CFILL= color. (If FILL were omitted, the CFILL= color would be used to fill the histogram bars instead.)
The HREF= option draws a reference line at the lower bound, and the HREFLABEL= option adds the label Lower Bound. The LHREF= option specifies a dashed line type for the reference line. The INSET statement adds an inset with the sample size positioned in the northeast corner of the plot.
In addition to displaying the beta curve, the BETA option requests a summary of the curve fit. This summary, which includes parameters for the curve and the observed and estimated quantiles, is shown in Output 4.21.2.
A sample program for this example, uniex12.sas, is available in the SAS Sample Library for Base SAS software.
Output 4.21.2: Summary of Fitted Beta Distribution
| Fitted Beta Distribution of Offsets |
| Parameters for Beta Distribution | ||
|---|---|---|
| Parameter | Symbol | Estimate |
| Threshold | Theta | 10 |
| Scale | Sigma | 0.5 |
| Shape | Alpha | 2.06832 |
| Shape | Beta | 6.022479 |
| Mean | 10.12782 | |
| Std Dev | 0.072339 | |
| Quantiles for Beta Distribution | ||
|---|---|---|
| Percent | Quantile | |
| Observed | Estimated | |
| 1.0 | 10.0180 | 10.0124 |
| 5.0 | 10.0310 | 10.0285 |
| 10.0 | 10.0380 | 10.0416 |
| 25.0 | 10.0670 | 10.0718 |
| 50.0 | 10.1220 | 10.1174 |
| 75.0 | 10.1750 | 10.1735 |
| 90.0 | 10.2255 | 10.2292 |
| 95.0 | 10.2780 | 10.2630 |
| 99.0 | 10.3220 | 10.3237 |