The UNIVARIATE Procedure

Kernel Density Estimates

You can use the KERNEL option to superimpose kernel density estimates on histograms. Smoothing the data distribution with a kernel density estimate can be more effective than using a histogram to identify features that might be obscured by the choice of histogram bins or sampling variation. A kernel density estimate can also be more effective than a parametric curve fit when the process distribution is multi-modal. See Example 4.23.

The general form of the kernel density estimator is

$\hat{f}_{\lambda }(x) = \frac{hv}{n\lambda } \sum ^ n_{i=1}K_{0}\left(\frac{x-x_{i}}{\lambda }\right)$

where

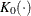$K_0 (\cdot )$ is the kernel function
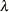$\lambda$ is the bandwidth
is the sample size
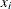is the 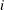th observation
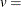vertical scaling factor

and

$v = \left\{ \begin{array}{ll} n & \mbox{for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right.$

The KERNEL option provides three kernel functions (): normal, quadratic, and triangular. You can specify the function with the K= kernel-option in parentheses after the KERNEL option. Values for the K= option are NORMAL, QUADRATIC, and TRIANGULAR (with aliases of N, Q, and T, respectively). By default, a normal kernel is used. The formulas for the kernel functions are

$\begin{array}{lll} \mbox{Normal} & K_0(t) = \frac{1}{\sqrt {2\pi }} \exp (-\frac{1}{2}t^{2}) & \mbox{for } -\infty < t < \infty \\ \mbox{Quadratic} & K_0(t) = \frac{3}{4}(1-t^2) & \mbox{for } |t| \leq 1 \\ \mbox{Triangular} & K_0(t) = 1-|t| & \mbox{for } |t| \leq 1 \end{array}$

The value of $\lambda$ , referred to as the bandwidth parameter, determines the degree of smoothness in the estimated density function. You specify $\lambda$ indirectly by specifying a standardized bandwidth with the C= kernel-option. If is the interquartile range and is the sample size, then is related to $\lambda$ by the formula

$\lambda = cQn^{-\frac{1}{5}}$

For a specific kernel function, the discrepancy between the density estimator $\hat{f}_{\lambda }(x)$ and the true density is measured by the mean integrated square error (MISE):

$\mbox{MISE}(\lambda ) = \int _{x}\{ E(\hat{f}_{\lambda }(x)) - f(x)\} ^{2}dx + \int _{x}var(\hat{f}_{\lambda }(x))dx$

The MISE is the sum of the integrated squared bias and the variance. An approximate mean integrated square error (AMISE) is:

$\mbox{AMISE}(\lambda ) = \frac{1}{4}\lambda ^{4} \left(\int _{t}t^{2}K(t)dt\right)^2 \int _ x\left(f^{\prime \prime }(x)\right)^2dx + \frac{1}{n\lambda }\int _{t}K(t)^2dt$

A bandwidth that minimizes AMISE can be derived by treating as the normal density that has parameters $\mu$ and $\sigma$ estimated by the sample mean and standard deviation. If you do not specify a bandwidth parameter or if you specify C=MISE, the bandwidth that minimizes AMISE is used. The value of AMISE can be used to compare different density estimates. You can also specify C=SJPI to select the bandwidth by using a plug-in formula of Sheather and Jones (Jones, Marron, and Sheather, 1996). For each estimate, the bandwidth parameter , the kernel function type, and the value of AMISE are reported in the SAS log.

The general kernel density estimates assume that the domain of the density to estimate can take on all values on a real line. However, sometimes the domain of a density is an interval bounded on one or both sides. For example, if a variable Y is a measurement of only positive values, then the kernel density curve should be bounded so that is zero for negative Y values. You can use the LOWER= and UPPER= kernel-options to specify the bounds.

The UNIVARIATE procedure uses a reflection technique to create the bounded kernel density curve, as described in Silverman (1986, pp. 30-31). It adds the reflections of the kernel density that are outside the boundary to the bounded kernel estimates. The general form of the bounded kernel density estimator is computed by replacing $K_{0}\left(\frac{x-x_{i}}{\lambda }\right)$ in the original equation with

$\left\{ K_0\left(\frac{x - x_ i}{\lambda }\right) + K_0\left(\frac{(x - x_ l) + (x_ i - x_ l)}{\lambda }\right) + K_0\left(\frac{(x_ u - x) + (x_ u - x_ i)}{\lambda }\right) \right\}$

where is the lower bound and is the upper bound.

Without a lower bound, $x_ l = -\infty$ and $K_0\left(\frac{(x-x_ l)+(x_ i-x_ l)}{\lambda }\right) = 0$ . Similarly, without an upper bound, $x_ u = \infty$ and $K_0\left(\frac{(x_ u-x)+(x_ u-x_ i)}{\lambda }\right) = 0$ .

When C=MISE is used with a bounded kernel density, the UNIVARIATE procedure uses a bandwidth that minimizes the AMISE for its corresponding unbounded kernel.