The UNIVARIATE Procedure
- Overview
-
Getting Started
-
Syntax
-
Details
Missing Values Rounding Descriptive Statistics Calculating the Mode Calculating Percentiles Tests for Location Confidence Limits for Parameters of the Normal Distribution Robust Estimators Creating Line Printer Plots Creating High-Resolution Graphics Using the CLASS Statement to Create Comparative Plots Positioning Insets Formulas for Fitted Continuous Distributions Goodness-of-Fit Tests Kernel Density Estimates Construction of Quantile-Quantile and Probability Plots Interpretation of Quantile-Quantile and Probability Plots Distributions for Probability and Q-Q Plots Estimating Shape Parameters Using Q-Q Plots Estimating Location and Scale Parameters Using Q-Q Plots Estimating Percentiles Using Q-Q Plots Input Data Sets OUT= Output Data Set in the OUTPUT Statement OUTHISTOGRAM= Output Data Set OUTKERNEL= Output Data Set OUTTABLE= Output Data Set Tables for Summary Statistics ODS Table Names ODS Tables for Fitted Distributions ODS Graphics Computational Resources
-
Examples
Computing Descriptive Statistics for Multiple Variables Calculating Modes Identifying Extreme Observations and Extreme Values Creating a Frequency Table Creating Plots for Line Printer Output Analyzing a Data Set With a FREQ Variable Saving Summary Statistics in an OUT= Output Data Set Saving Percentiles in an Output Data Set Computing Confidence Limits for the Mean, Standard Deviation, and Variance Computing Confidence Limits for Quantiles and Percentiles Computing Robust Estimates Testing for Location Performing a Sign Test Using Paired Data Creating a Histogram Creating a One-Way Comparative Histogram Creating a Two-Way Comparative Histogram Adding Insets with Descriptive Statistics Binning a Histogram Adding a Normal Curve to a Histogram Adding Fitted Normal Curves to a Comparative Histogram Fitting a Beta Curve Fitting Lognormal, Weibull, and Gamma Curves Computing Kernel Density Estimates Fitting a Three-Parameter Lognormal Curve Annotating a Folded Normal Curve Creating Lognormal Probability Plots Creating a Histogram to Display Lognormal Fit Creating a Normal Quantile Plot Adding a Distribution Reference Line Interpreting a Normal Quantile Plot Estimating Three Parameters from Lognormal Quantile Plots Estimating Percentiles from Lognormal Quantile Plots Estimating Parameters from Lognormal Quantile Plots Comparing Weibull Quantile Plots Creating a Cumulative Distribution Plot Creating a P-P Plot
- References
Example 4.27 Creating a Histogram to Display Lognormal Fit
This example uses the data set Aircraft from Example 4.26 to illustrate how to display a lognormal fit with a histogram. To determine whether the lognormal distribution is an appropriate model for a distribution, you should consider the graphical fit as well as conduct goodness-of-fit tests. The following statements fit a lognormal distribution and display the density curve on a histogram:
title 'Distribution of Position Deviations';
ods graphics off;
ods select Lognormal.ParameterEstimates Lognormal.GoodnessOfFit MyPlot;
proc univariate data=Aircraft;
var Deviation;
histogram / lognormal(w=3 theta=est)
vaxis = axis1
name = 'MyPlot';
inset n mean (5.3) std='Std Dev' (5.3) skewness (5.3) /
pos = ne header = 'Summary Statistics';
axis1 label=(a=90 r=0);
run;
The ODS SELECT statement restricts the output to the "ParameterEstimates" and "GoodnessOfFit" tables; see the section ODS Table Names. The LOGNORMAL primary option superimposes a fitted curve on the histogram in Output 4.27.1. The W= option specifies the line width for the curve. The INSET statement specifies that the mean, standard deviation, and skewness be displayed in an inset in the northeast corner of the plot. Note that the default value of the threshold parameter 
is zero. In applications where the threshold is not zero, you can specify with the THETA= option. The variable Deviation includes values that are less than the default threshold; therefore, the option THETA= EST is used.
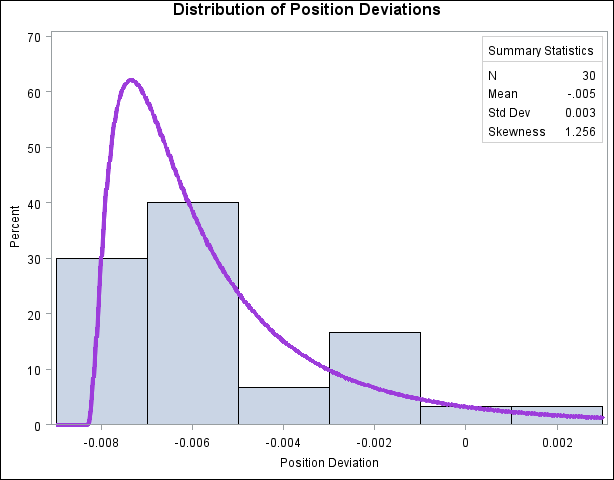
Output 4.27.2 provides three EDF goodness-of-fit tests for the lognormal distribution: the Anderson-Darling, the Cramér-von Mises, and the Kolmogorov-Smirnov tests. The null hypothesis for the three tests is that a lognormal distribution holds for the sample data.
| Distribution of Position Deviations |
| Parameters for Lognormal Distribution | ||
|---|---|---|
| Parameter | Symbol | Estimate |
| Threshold | Theta | -0.00834 |
| Scale | Zeta | -6.14382 |
| Shape | Sigma | 0.882225 |
| Mean | -0.00517 | |
| Std Dev | 0.003438 | |
| Goodness-of-Fit Tests for Lognormal Distribution | ||||
|---|---|---|---|---|
| Test | Statistic | p Value | ||
| Kolmogorov-Smirnov | D | 0.09419634 | Pr > D | >0.500 |
| Cramer-von Mises | W-Sq | 0.02919815 | Pr > W-Sq | >0.500 |
| Anderson-Darling | A-Sq | 0.21606642 | Pr > A-Sq | >0.500 |
The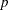 
-values for all three tests are greater than 0.5, so the null hypothesis is not rejected. The tests support the conclusion that the two-parameter lognormal distribution with scale parameter 
and shape parameter 
provides a good model for the distribution of position deviations. For further discussion of goodness-of-fit interpretation, see the section Goodness-of-Fit Tests.
A sample program for this example, uniex16.sas, is available in the SAS Sample Library for Base SAS software.