The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing Values Rounding Descriptive Statistics Calculating the Mode Calculating Percentiles Tests for Location Confidence Limits for Parameters of the Normal Distribution Robust Estimators Creating Line Printer Plots Creating High-Resolution Graphics Using the CLASS Statement to Create Comparative Plots Positioning Insets Formulas for Fitted Continuous Distributions Goodness-of-Fit Tests Kernel Density Estimates Construction of Quantile-Quantile and Probability Plots Interpretation of Quantile-Quantile and Probability Plots Distributions for Probability and Q-Q Plots Estimating Shape Parameters Using Q-Q Plots Estimating Location and Scale Parameters Using Q-Q Plots Estimating Percentiles Using Q-Q Plots Input Data Sets OUT= Output Data Set in the OUTPUT Statement OUTHISTOGRAM= Output Data Set OUTKERNEL= Output Data Set OUTTABLE= Output Data Set Tables for Summary Statistics ODS Table Names ODS Tables for Fitted Distributions ODS Graphics Computational Resources
Missing Values Rounding Descriptive Statistics Calculating the Mode Calculating Percentiles Tests for Location Confidence Limits for Parameters of the Normal Distribution Robust Estimators Creating Line Printer Plots Creating High-Resolution Graphics Using the CLASS Statement to Create Comparative Plots Positioning Insets Formulas for Fitted Continuous Distributions Goodness-of-Fit Tests Kernel Density Estimates Construction of Quantile-Quantile and Probability Plots Interpretation of Quantile-Quantile and Probability Plots Distributions for Probability and Q-Q Plots Estimating Shape Parameters Using Q-Q Plots Estimating Location and Scale Parameters Using Q-Q Plots Estimating Percentiles Using Q-Q Plots Input Data Sets OUT= Output Data Set in the OUTPUT Statement OUTHISTOGRAM= Output Data Set OUTKERNEL= Output Data Set OUTTABLE= Output Data Set Tables for Summary Statistics ODS Table Names ODS Tables for Fitted Distributions ODS Graphics Computational Resources -
Examples
 Computing Descriptive Statistics for Multiple Variables Calculating Modes Identifying Extreme Observations and Extreme Values Creating a Frequency Table Creating Plots for Line Printer Output Analyzing a Data Set With a FREQ Variable Saving Summary Statistics in an OUT= Output Data Set Saving Percentiles in an Output Data Set Computing Confidence Limits for the Mean, Standard Deviation, and Variance Computing Confidence Limits for Quantiles and Percentiles Computing Robust Estimates Testing for Location Performing a Sign Test Using Paired Data Creating a Histogram Creating a One-Way Comparative Histogram Creating a Two-Way Comparative Histogram Adding Insets with Descriptive Statistics Binning a Histogram Adding a Normal Curve to a Histogram Adding Fitted Normal Curves to a Comparative Histogram Fitting a Beta Curve Fitting Lognormal, Weibull, and Gamma Curves Computing Kernel Density Estimates Fitting a Three-Parameter Lognormal Curve Annotating a Folded Normal Curve Creating Lognormal Probability Plots Creating a Histogram to Display Lognormal Fit Creating a Normal Quantile Plot Adding a Distribution Reference Line Interpreting a Normal Quantile Plot Estimating Three Parameters from Lognormal Quantile Plots Estimating Percentiles from Lognormal Quantile Plots Estimating Parameters from Lognormal Quantile Plots Comparing Weibull Quantile Plots Creating a Cumulative Distribution Plot Creating a P-P Plot
Computing Descriptive Statistics for Multiple Variables Calculating Modes Identifying Extreme Observations and Extreme Values Creating a Frequency Table Creating Plots for Line Printer Output Analyzing a Data Set With a FREQ Variable Saving Summary Statistics in an OUT= Output Data Set Saving Percentiles in an Output Data Set Computing Confidence Limits for the Mean, Standard Deviation, and Variance Computing Confidence Limits for Quantiles and Percentiles Computing Robust Estimates Testing for Location Performing a Sign Test Using Paired Data Creating a Histogram Creating a One-Way Comparative Histogram Creating a Two-Way Comparative Histogram Adding Insets with Descriptive Statistics Binning a Histogram Adding a Normal Curve to a Histogram Adding Fitted Normal Curves to a Comparative Histogram Fitting a Beta Curve Fitting Lognormal, Weibull, and Gamma Curves Computing Kernel Density Estimates Fitting a Three-Parameter Lognormal Curve Annotating a Folded Normal Curve Creating Lognormal Probability Plots Creating a Histogram to Display Lognormal Fit Creating a Normal Quantile Plot Adding a Distribution Reference Line Interpreting a Normal Quantile Plot Estimating Three Parameters from Lognormal Quantile Plots Estimating Percentiles from Lognormal Quantile Plots Estimating Parameters from Lognormal Quantile Plots Comparing Weibull Quantile Plots Creating a Cumulative Distribution Plot Creating a P-P Plot - References
| QQPLOT Statement |
- QQPLOT <variables> < / options> ;
The QQPLOT statement creates quantile-quantile plots (Q-Q plots) and compares ordered variable values with quantiles of a specified theoretical distribution. If the data distribution matches the theoretical distribution, the points on the plot form a linear pattern. Thus, you can use a Q-Q plot to determine how well a theoretical distribution models a set of measurements.
Q-Q plots are similar to probability plots, which you can create with the PROBPLOT statement. Q-Q plots are preferable for graphical estimation of distribution parameters, whereas probability plots are preferable for graphical estimation of percentiles.
You can use any number of QQPLOT statements in the UNIVARIATE procedure. The components of the QQPLOT statement are as follows.
- variables
-
are the variables for which Q-Q plots are created. If you specify a VAR statement, the variables must also be listed in the VAR statement. Otherwise, the variables can be any numeric variables in the input data set. If you do not specify a list of variables, then by default the procedure creates a Q-Q plot for each variable listed in the VAR statement, or for each numeric variable in the DATA= data set if you do not specify a VAR statement. For example, each of the following QQPLOT statements produces two Q-Q plots, one for Length and one for Width:
proc univariate data=Measures; var Length Width; qqplot; proc univariate data=Measures; qqplot Length Width; run;
- options
-
specify the theoretical distribution for the plot or add features to the plot. If you specify more than one variable, the options apply equally to each variable. Specify all options after the slash (/) in the QQPLOT statement. You can specify only one option that names the distribution in each QQPLOT statement, but you can specify any number of other options. The distributions available are the beta, exponential, gamma, lognormal, normal, two-parameter Weibull, and three-parameter Weibull. By default, the procedure produces a plot for the normal distribution.
In the following example, the NORMAL option requests a normal Q-Q plot for each variable. The MU= and SIGMA= normal-options request a distribution reference line with intercept 10 and slope 0.3 for each plot, corresponding to a normal distribution with mean
 and standard deviation
and standard deviation  . The SQUARE option displays the plot in a square frame, and the CTEXT= option specifies the text color.
. The SQUARE option displays the plot in a square frame, and the CTEXT= option specifies the text color. proc univariate data=measures; qqplot length1 length2 / normal(mu=10 sigma=0.3) square ctext=blue; run;Table 4.93 through Table 4.106 list the QQPLOT options by function. For complete descriptions, see the sections Dictionary of Options and Dictionary of Common Options.
Options can be any of the following:
primary options
secondary options
general options
Distribution Options
Table 4.93 lists primary options for requesting a theoretical distribution. See the section Distributions for Probability and Q-Q Plots for detailed descriptions of these distributions.
Option |
Description |
|---|---|
specifies beta Q-Q plot for shape parameters |
|
specifies exponential Q-Q plot |
|
specifies gamma Q-Q plot for shape parameter |
|
specifies gumbel Q-Q plot |
|
specifies lognormal Q-Q plot for shape parameter |
|
specifies normal Q-Q plot |
|
specifies generalized Pareto Q-Q plot for shape parameter |
|
specifies power function Q-Q plot for shape parameter |
|
specifies Rayleigh Q-Q plot |
|
specifies three-parameter Weibull Q-Q plot for shape parameter |
|
specifies two-parameter Weibull Q-Q plot |
Table 4.94 through Table 4.105 list secondary options that specify distribution parameters and control the display of a distribution reference line. Specify these options in parentheses after the distribution keyword. For example, you can request a normal Q-Q plot with a distribution reference line by specifying the NORMAL option as follows:
proc univariate; qqplot Length / normal(mu=10 sigma=0.3 color=red); run;
The MU= and SIGMA= normal-options display a distribution reference line that corresponds to the normal distribution with mean 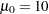 and standard deviation
and standard deviation 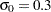 , and the COLOR= normal-option specifies the color for the line.
, and the COLOR= normal-option specifies the color for the line.
Option |
Description |
|---|---|
specifies color of distribution reference line |
|
specifies line type of distribution reference line |
|
specifies width of distribution reference line |
Option |
Description |
|---|---|
specifies mandatory shape parameter |
|
specifies mandatory shape parameter |
|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies mandatory shape parameter |
|
specifies change in successive estimates of |
|
specifies initial value for |
|
specifies maximum number of iterations in the Newton-Raphson approximation of |
|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies mandatory shape parameter |
|
specifies slope of distribution reference line |
|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies mandatory shape parameter |
|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies mandatory shape parameter |
|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies mandatory shape parameter c |
|
specifies |
|
specifies |
Option |
Description |
|---|---|
specifies |
|
specifies |
|
specifies slope of distribution reference line |
|
specifies known lower threshold |
General Options
Table 4.106 summarizes general options for enhancing Q-Q plots.
Option |
Description |
|---|---|
applies annotation requested in ANNOTATE= data set to key cell only |
|
specifies annotate data set |
|
specifies color for axis |
|
specifies color for frame |
|
specifies color for filling frame for row labels |
|
specifies color for filling frame for column labels |
|
specifies color for grid lines |
|
specifies color for HREF= lines |
|
specifies table of contents entry for Q-Q plot grouping |
|
specifies color for text |
|
specifies color for VREF= lines |
|
specifies description for plot in graphics catalog |
|
specifies software font for text |
|
creates a grid |
|
specifies height of text used outside framed areas |
|
specifies number of horizontal minor tick marks |
|
specifies reference lines perpendicular to the horizontal axis |
|
specifies labels for HREF= lines |
|
specifies vertical position of labels for HREF= lines |
|
specifies software font for text inside framed areas |
|
specifies height of text inside framed areas |
|
specifies distance between tiles |
|
specifies a line type for grid lines |
|
specifies line style for HREF= lines |
|
specifies line style for VREF= lines |
|
adjusts sample size when computing percentiles |
|
specifies name for plot in graphics catalog |
|
specifies number of columns in comparative Q-Q plot |
|
suppresses frame around plotting area |
|
suppresses label for horizontal axis |
|
suppresses label for vertical axis |
|
suppresses tick marks and tick mark labels for vertical axis |
|
specifies number of rows in comparative Q-Q plot |
|
displays a nonlinear percentile axis |
|
requests minor tick marks for percentile axis |
|
replaces theoretical quantiles with percentiles |
|
adjusts ranks when computing percentiles |
|
switches horizontal and vertical axes |
|
displays plot in square format |
|
specifies AXIS statement for vertical axis |
|
specifies label for vertical axis |
|
specifies number of vertical minor tick marks |
|
specifies reference lines perpendicular to the vertical axis |
|
specifies labels for VREF= lines |
|
specifies horizontal position of labels for VREF= lines |
|
specifies line thickness for axes and frame |
|
specifies line thickness for grid |
Dictionary of Options
The following entries provide detailed descriptions of options in the QQPLOT statement. Options marked with † are applicable only when traditional graphics are produced. See the section Dictionary of Common Options for detailed descriptions of options common to all plot statements.
- ALPHA=value-list | EST
-
specifies the mandatory shape parameter
 for quantile plots requested with the BETA, GAMMA, PARETO, and POWER options. Enclose the ALPHA= option in parentheses after the distribution keyword. If you specify ALPHA=EST, a maximum likelihood estimate is computed for
for quantile plots requested with the BETA, GAMMA, PARETO, and POWER options. Enclose the ALPHA= option in parentheses after the distribution keyword. If you specify ALPHA=EST, a maximum likelihood estimate is computed for  .
. - BETA(ALPHA=value | EST BETA=value | EST <beta-options>)
-
creates a beta quantile plot for each combination of the required shape parameters
 and
and 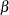 specified by the required ALPHA= and BETA= beta-options. If you specify ALPHA=EST and BETA=EST, the procedure creates a plot based on maximum likelihood estimates for
specified by the required ALPHA= and BETA= beta-options. If you specify ALPHA=EST and BETA=EST, the procedure creates a plot based on maximum likelihood estimates for  and
and 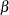 . You can specify the SCALE= beta-option as an alias for the SIGMA= beta-option and the THRESHOLD= beta-option as an alias for the THETA= beta-option. To create a plot that is based on maximum likelihood estimates for
. You can specify the SCALE= beta-option as an alias for the SIGMA= beta-option and the THRESHOLD= beta-option as an alias for the THETA= beta-option. To create a plot that is based on maximum likelihood estimates for  and
and 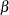 , specify ALPHA=EST and BETA=EST. See the section Beta Distribution for details.
, specify ALPHA=EST and BETA=EST. See the section Beta Distribution for details. To obtain graphical estimates of
 and
and 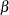 , specify lists of values in the ALPHA= and BETA= beta-options and select the combination of
, specify lists of values in the ALPHA= and BETA= beta-options and select the combination of  and
and 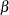 that most nearly linearizes the point pattern. To assess the point pattern, you can add a diagonal distribution reference line corresponding to lower threshold parameter
that most nearly linearizes the point pattern. To assess the point pattern, you can add a diagonal distribution reference line corresponding to lower threshold parameter  and scale parameter
and scale parameter  with the THETA= and SIGMA= beta-options. Alternatively, you can add a line that corresponds to estimated values of
with the THETA= and SIGMA= beta-options. Alternatively, you can add a line that corresponds to estimated values of  and
and  with the beta-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the beta distribution with parameters
with the beta-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the beta distribution with parameters  ,
, 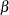 ,
,  , and
, and  is a good fit.
is a good fit. - BETA=value-list | EST
- B=value | EST
specifies the mandatory shape parameter
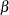 for quantile plots requested with the BETA option. Enclose the BETA= option in parentheses after the BETA option. If you specify BETA=EST, a maximum likelihood estimate is computed for
for quantile plots requested with the BETA option. Enclose the BETA= option in parentheses after the BETA option. If you specify BETA=EST, a maximum likelihood estimate is computed for 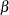 .
. - C=value-list | EST
-
specifies the shape parameter
 for quantile plots requested with the WEIBULL and WEIBULL2 options. Enclose this option in parentheses after the WEIBULL or WEIBULL2 option. C= is a required Weibull-option in the WEIBULL option; in this situation, it accepts a list of values, or if you specify C=EST, a maximum likelihood estimate is computed for
for quantile plots requested with the WEIBULL and WEIBULL2 options. Enclose this option in parentheses after the WEIBULL or WEIBULL2 option. C= is a required Weibull-option in the WEIBULL option; in this situation, it accepts a list of values, or if you specify C=EST, a maximum likelihood estimate is computed for  . You can optionally specify C=value or C=EST as a Weibull2-option with the WEIBULL2 option to request a distribution reference line; in this situation, you must also specify Weibull2-option SIGMA=value or SIGMA=EST.
. You can optionally specify C=value or C=EST as a Weibull2-option with the WEIBULL2 option to request a distribution reference line; in this situation, you must also specify Weibull2-option SIGMA=value or SIGMA=EST. - † CGRID=color
-
specifies the color for grid lines when a grid displays on the plot. This option also produces a grid.
- EXPONENTIAL<(exponential-options)>
- EXP<(exponential-options)>
-
creates an exponential quantile plot. To assess the point pattern, add a diagonal distribution reference line corresponding to
 and
and  with the THETA= and SIGMA= exponential-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter
with the THETA= and SIGMA= exponential-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter  and the scale parameter
and the scale parameter  with the exponential-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the exponential distribution with parameters
with the exponential-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the exponential distribution with parameters  and
and  is a good fit. You can specify the SCALE= exponential-option as an alias for the SIGMA= exponential-option and the THRESHOLD= exponential-option as an alias for the THETA= exponential-option. See the section Exponential Distribution for details.
is a good fit. You can specify the SCALE= exponential-option as an alias for the SIGMA= exponential-option and the THRESHOLD= exponential-option as an alias for the THETA= exponential-option. See the section Exponential Distribution for details. - GAMMA(ALPHA=value | EST <gamma-options>)
-
creates a gamma quantile plot for each value of the shape parameter
 given by the mandatory ALPHA= gamma-option. If you specify ALPHA=EST, the procedure creates a plot based on a maximum likelihood estimate for
given by the mandatory ALPHA= gamma-option. If you specify ALPHA=EST, the procedure creates a plot based on a maximum likelihood estimate for  . To obtain a graphical estimate of
. To obtain a graphical estimate of  , specify a list of values for the ALPHA= gamma-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to
, specify a list of values for the ALPHA= gamma-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to  and
and  with the THETA= and SIGMA= gamma-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter
with the THETA= and SIGMA= gamma-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter  and the scale parameter
and the scale parameter  with the gamma-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the gamma distribution with parameters
with the gamma-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the gamma distribution with parameters  ,
,  , and
, and  is a good fit. You can specify the SCALE= gamma-option as an alias for the SIGMA= gamma-option and the THRESHOLD= gamma-option as an alias for the THETA= gamma-option. See the section Gamma Distribution for details.
is a good fit. You can specify the SCALE= gamma-option as an alias for the SIGMA= gamma-option and the THRESHOLD= gamma-option as an alias for the THETA= gamma-option. See the section Gamma Distribution for details. - GRID
-
displays a grid of horizontal lines positioned at major tick marks on the vertical axis.
- GUMBEL<(Gumbel-options)>
-
creates a Gumbel quantile plot. To assess the point pattern, add a diagonal distribution reference line corresponding to
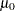 and
and  with the MU= and SIGMA= Gumbel-options. Alternatively, you can add a line corresponding to estimated values of the location parameter
with the MU= and SIGMA= Gumbel-options. Alternatively, you can add a line corresponding to estimated values of the location parameter 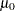 and the scale parameter
and the scale parameter  with the Gumbel-options MU=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the exponential distribution with parameters
with the Gumbel-options MU=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the exponential distribution with parameters 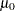 and
and  is a good fit. See the section Gumbel Distribution for details.
is a good fit. See the section Gumbel Distribution for details. - † LGRID=linetype
-
specifies the line type for the grid requested by the GRID option. By default, LGRID=1, which produces a solid line. The LGRID= option also produces a grid.
- LOGNORMAL(SIGMA=value | EST <lognormal-options>)
- LNORM(SIGMA=value | EST <lognormal-options>)
-
creates a lognormal quantile plot for each value of the shape parameter
 given by the mandatory SIGMA= lognormal-option. If you specify SIGMA=EST, the procedure creates a plot based on a maximum likelihood estimate for
given by the mandatory SIGMA= lognormal-option. If you specify SIGMA=EST, the procedure creates a plot based on a maximum likelihood estimate for  . To obtain a graphical estimate of
. To obtain a graphical estimate of  , specify a list of values for the SIGMA= lognormal-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to
, specify a list of values for the SIGMA= lognormal-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to  and
and 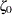 with the THETA= and ZETA= lognormal-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter
with the THETA= and ZETA= lognormal-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter  and the scale parameter
and the scale parameter 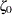 with the lognormal-options THETA=EST and ZETA=EST. Agreement between the reference line and the point pattern indicates that the lognormal distribution with parameters
with the lognormal-options THETA=EST and ZETA=EST. Agreement between the reference line and the point pattern indicates that the lognormal distribution with parameters  ,
,  , and
, and 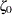 is a good fit. You can specify the THRESHOLD= lognormal-option as an alias for the THETA= lognormal-option and the SCALE= lognormal-option as an alias for the ZETA= lognormal-option. See the section Lognormal Distribution for details, and see Example 4.31 through Example 4.33 for examples that use the LOGNORMAL option.
is a good fit. You can specify the THRESHOLD= lognormal-option as an alias for the THETA= lognormal-option and the SCALE= lognormal-option as an alias for the ZETA= lognormal-option. See the section Lognormal Distribution for details, and see Example 4.31 through Example 4.33 for examples that use the LOGNORMAL option. - MU=value | EST
-
specifies the mean
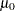 for a quantile plot requested with the GUMBEL and NORMAL options. Enclose MU= in parentheses after the distribution keyword. You can specify MU=EST to request a distribution reference line with
for a quantile plot requested with the GUMBEL and NORMAL options. Enclose MU= in parentheses after the distribution keyword. You can specify MU=EST to request a distribution reference line with 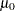 equal to the sample mean with the normal distribution. If you specify MU=EST for the Gumbel distribution, the procedure computes a maximum likelihood estimate.
equal to the sample mean with the normal distribution. If you specify MU=EST for the Gumbel distribution, the procedure computes a maximum likelihood estimate. - NADJ=value
-
specifies the adjustment value added to the sample size in the calculation of theoretical percentiles. By default, NADJ=
 . Refer to Chambers et al. (1983) for additional information.
. Refer to Chambers et al. (1983) for additional information. - NORMAL<(normal-options)>
-
creates a normal quantile plot. This is the default if you omit a distribution option. To assess the point pattern, you can add a diagonal distribution reference line corresponding to
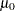 and
and  with the MU= and SIGMA= normal-options. Alternatively, you can add a line corresponding to estimated values of
with the MU= and SIGMA= normal-options. Alternatively, you can add a line corresponding to estimated values of 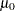 and
and  with the normal-options MU=EST and SIGMA=EST; the estimates of the mean
with the normal-options MU=EST and SIGMA=EST; the estimates of the mean 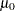 and the standard deviation
and the standard deviation  are the sample mean and sample standard deviation. Agreement between the reference line and the point pattern indicates that the normal distribution with parameters
are the sample mean and sample standard deviation. Agreement between the reference line and the point pattern indicates that the normal distribution with parameters 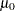 and
and  is a good fit. See the section Normal Distribution for details, and see Example 4.28 and Example 4.30 for examples that use the NORMAL option.
is a good fit. See the section Normal Distribution for details, and see Example 4.28 and Example 4.30 for examples that use the NORMAL option. - PARETO(ALPHA=value | EST <Pareto-options>)
-
creates a generalized Pareto quantile plot for each value of the shape parameter
 given by the mandatory ALPHA= Pareto-option. If you specify ALPHA=EST, the procedure creates a plot based on a maximum likelihood estimate for
given by the mandatory ALPHA= Pareto-option. If you specify ALPHA=EST, the procedure creates a plot based on a maximum likelihood estimate for  . To obtain a graphical estimate of
. To obtain a graphical estimate of  , specify a list of values for the ALPHA= Pareto-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to
, specify a list of values for the ALPHA= Pareto-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to  and
and  with the THETA= and SIGMA= Pareto-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter
with the THETA= and SIGMA= Pareto-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter  and the scale parameter
and the scale parameter  with the Pareto-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the generalized Pareto distribution with parameters
with the Pareto-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the generalized Pareto distribution with parameters  ,
,  , and
, and  is a good fit. See the section Generalized Pareto Distribution for details.
is a good fit. See the section Generalized Pareto Distribution for details. - PCTLAXIS<(axis-options)>
-
adds a nonlinear percentile axis along the frame of the Q-Q plot opposite the theoretical quantile axis. The added axis is identical to the axis for probability plots produced with the PROBPLOT statement. When using the PCTLAXIS option, you must specify HREF= values in quantile units, and you cannot use the NOFRAME option. You can specify the following axis-options:
Table 4.107 PCTLAXIS Axis Options Option
Description
CGRID=
specifies color for grid lines
GRID
draws grid lines at major percentiles
LABEL='string'
specifies label for percentile axis
LGRID=linetype
specifies line type for grid
WGRID=n
specifies line thickness for grid
- † PCTLMINOR
-
requests minor tick marks for the percentile axis when you specify PCTLAXIS. The HMINOR option overrides the PCTLMINOR option.
- PCTLSCALE
-
requests scale labels for the theoretical quantile axis in percentile units, resulting in a nonlinear axis scale. Tick marks are drawn uniformly across the axis based on the quantile scale. In all other respects, the plot remains the same, and you must specify HREF= values in quantile units. For a true nonlinear axis, use the PCTLAXIS option or use the PROBPLOT statement.
- POWER(ALPHA=value | EST <power-options>)
-
creates a power function quantile plot for each value of the shape parameter
 given by the mandatory ALPHA= power-option. If you specify ALPHA=EST, the procedure creates a plot based on a maximum likelihood estimate for
given by the mandatory ALPHA= power-option. If you specify ALPHA=EST, the procedure creates a plot based on a maximum likelihood estimate for  . To obtain a graphical estimate of
. To obtain a graphical estimate of  , specify a list of values for the ALPHA= power-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to
, specify a list of values for the ALPHA= power-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to  and
and  with the THETA= and SIGMA= power-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter
with the THETA= and SIGMA= power-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter  and the scale parameter
and the scale parameter  with the power-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the power function distribution with parameters
with the power-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the power function distribution with parameters  ,
,  , and
, and  is a good fit. See the section Power Function Distribution for details.
is a good fit. See the section Power Function Distribution for details. - RAYLEIGH<(Rayleigh-options)>
-
creates a Rayleigh quantile plot. To assess the point pattern, add a diagonal distribution reference line corresponding to
 and
and  with the THETA= and SIGMA= Rayleigh-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter
with the THETA= and SIGMA= Rayleigh-options. Alternatively, you can add a line corresponding to estimated values of the threshold parameter  and the scale parameter
and the scale parameter  with the Rayleigh-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the exponential distribution with parameters
with the Rayleigh-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the exponential distribution with parameters  and
and  is a good fit. See the section Rayleigh Distribution for details.
is a good fit. See the section Rayleigh Distribution for details. - RANKADJ=value
-
specifies the adjustment value added to the ranks in the calculation of theoretical percentiles. By default, RANKADJ=
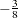 , as recommended by Blom (1958). Refer to Chambers et al. (1983) for additional information.
, as recommended by Blom (1958). Refer to Chambers et al. (1983) for additional information. - ROTATE
-
switches the horizontal and vertical axes so that the theoretical quantiles are plotted vertically while the data are plotted horizontally. Regardless of whether the plot has been rotated, horizontal axis options (such as HAXIS=) still refer to the horizontal axis, and vertical axis options (such as VAXIS=) still refer to the vertical axis. All other options that depend on axis placement adjust to the rotated axes.
- SIGMA=value | EST
-
specifies the parameter
 , where
, where 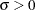 . Alternatively, you can specify SIGMA=EST to request a maximum likelihood estimate for
. Alternatively, you can specify SIGMA=EST to request a maximum likelihood estimate for  . The interpretation and use of the SIGMA= option depend on the distribution option with which it is used, as summarized in Table 4.108. Enclose this option in parentheses after the distribution option.
. The interpretation and use of the SIGMA= option depend on the distribution option with which it is used, as summarized in Table 4.108. Enclose this option in parentheses after the distribution option. Table 4.108 Uses of the SIGMA= Option Distribution Option
Use of the SIGMA= Option
BETA EXPONENTIAL GAMMA PARETO POWER RAYLEIGH WEIBULL
THETA=
 and SIGMA=
and SIGMA= request a distribution reference line corresponding to
request a distribution reference line corresponding to  and
and  .
. GUMBEL
MU=
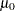 and SIGMA=
and SIGMA= request a distribution reference line corresponding to
request a distribution reference line corresponding to 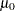 and
and  .
. LOGNORMAL
SIGMA=
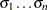 requests
requests  quantile plots with shape parameters
quantile plots with shape parameters 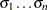 . The SIGMA= option must be specified.
. The SIGMA= option must be specified. NORMAL
MU=
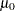 and SIGMA=
and SIGMA= request a distribution reference line corresponding to
request a distribution reference line corresponding to 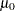 and
and  . SIGMA=EST requests a line with
. SIGMA=EST requests a line with  equal to the sample standard deviation.
equal to the sample standard deviation. WEIBULL2
SIGMA=
 and C=
and C=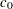 request a distribution reference line corresponding to
request a distribution reference line corresponding to  and
and 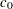 .
. - SLOPE=value | EST
-
specifies the slope for a distribution reference line requested with the LOGNORMAL and WEIBULL2 options. Enclose the SLOPE= option in parentheses after the distribution option. When you use the SLOPE= lognormal-option with the LOGNORMAL option, you must also specify a threshold parameter value
 with the THETA= lognormal-option to request the line. The SLOPE= lognormal-option is an alternative to the ZETA= lognormal-option for specifying
with the THETA= lognormal-option to request the line. The SLOPE= lognormal-option is an alternative to the ZETA= lognormal-option for specifying 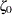 , because the slope is equal to
, because the slope is equal to  .
. When you use the SLOPE= Weibull2-option with the WEIBULL2 option, you must also specify a scale parameter value
 with the SIGMA= Weibull2-option to request the line. The SLOPE= Weibull2-option is an alternative to the C= Weibull2-option for specifying
with the SIGMA= Weibull2-option to request the line. The SLOPE= Weibull2-option is an alternative to the C= Weibull2-option for specifying 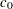 , because the slope is equal to
, because the slope is equal to  .
. For example, the first and second QQPLOT statements produce the same quantile plots and the third and fourth QQPLOT statements produce the same quantile plots:
proc univariate data=Measures; qqplot Width / lognormal(sigma=2 theta=0 zeta=0); qqplot Width / lognormal(sigma=2 theta=0 slope=1); qqplot Width / weibull2(sigma=2 theta=0 c=.25); qqplot Width / weibull2(sigma=2 theta=0 slope=4);
- SQUARE
-
displays the quantile plot in a square frame. By default, the frame is rectangular.
- THETA=value | EST
- THRESHOLD=value | EST
-
specifies the lower threshold parameter
 for plots requested with the BETA, EXPONENTIAL, GAMMA, PARETO, POWER, RAYLEIGH, LOGNORMAL, WEIBULL, and WEIBULL2 options. Enclose the THETA= option in parentheses after a distribution option. When used with the WEIBULL2 option, the THETA= option specifies the known lower threshold
for plots requested with the BETA, EXPONENTIAL, GAMMA, PARETO, POWER, RAYLEIGH, LOGNORMAL, WEIBULL, and WEIBULL2 options. Enclose the THETA= option in parentheses after a distribution option. When used with the WEIBULL2 option, the THETA= option specifies the known lower threshold  , for which the default is 0. When used with the other distribution options, the THETA= option specifies
, for which the default is 0. When used with the other distribution options, the THETA= option specifies  for a distribution reference line; alternatively in this situation, you can specify THETA=EST to request a maximum likelihood estimate for
for a distribution reference line; alternatively in this situation, you can specify THETA=EST to request a maximum likelihood estimate for  . To request the line, you must also specify a scale parameter.
. To request the line, you must also specify a scale parameter. - WEIBULL(C=value | EST <Weibull-options>)
- WEIB(C=value | EST <Weibull-options>)
-
creates a three-parameter Weibull quantile plot for each value of the required shape parameter
 specified by the mandatory C= Weibull-option. To create a plot that is based on a maximum likelihood estimate for
specified by the mandatory C= Weibull-option. To create a plot that is based on a maximum likelihood estimate for  , specify C=EST. To obtain a graphical estimate of
, specify C=EST. To obtain a graphical estimate of  , specify a list of values in the C= Weibull-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to
, specify a list of values in the C= Weibull-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to  and
and  with the THETA= and SIGMA= Weibull-options. Alternatively, you can add a line corresponding to estimated values of
with the THETA= and SIGMA= Weibull-options. Alternatively, you can add a line corresponding to estimated values of  and
and  with the Weibull-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the Weibull distribution with parameters
with the Weibull-options THETA=EST and SIGMA=EST. Agreement between the reference line and the point pattern indicates that the Weibull distribution with parameters  ,
,  , and
, and  is a good fit. You can specify the SCALE= Weibull-option as an alias for the SIGMA= Weibull-option and the THRESHOLD= Weibull-option as an alias for the THETA= Weibull-option. See Example 4.34.
is a good fit. You can specify the SCALE= Weibull-option as an alias for the SIGMA= Weibull-option and the THRESHOLD= Weibull-option as an alias for the THETA= Weibull-option. See Example 4.34. - WEIBULL2<(Weibull2-options)>
- W2<(Weibull2-options)>
-
creates a two-parameter Weibull quantile plot. You should use the WEIBULL2 option when your data have a known lower threshold
 , which is 0 by default. To specify the threshold value
, which is 0 by default. To specify the threshold value  , use the THETA= Weibull2-option. By default, THETA=0. An advantage of the two-parameter Weibull plot over the three-parameter Weibull plot is that the parameters
, use the THETA= Weibull2-option. By default, THETA=0. An advantage of the two-parameter Weibull plot over the three-parameter Weibull plot is that the parameters  and
and  can be estimated from the slope and intercept of the point pattern. A disadvantage is that the two-parameter Weibull distribution applies only in situations where the threshold parameter is known. To obtain a graphical estimate of
can be estimated from the slope and intercept of the point pattern. A disadvantage is that the two-parameter Weibull distribution applies only in situations where the threshold parameter is known. To obtain a graphical estimate of  , specify a list of values for the THETA= Weibull2-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to
, specify a list of values for the THETA= Weibull2-option and select the value that most nearly linearizes the point pattern. To assess the point pattern, add a diagonal distribution reference line corresponding to  and
and 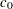 with the SIGMA= and C= Weibull2-options. Alternatively, you can add a distribution reference line corresponding to estimated values of
with the SIGMA= and C= Weibull2-options. Alternatively, you can add a distribution reference line corresponding to estimated values of  and
and 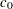 with the Weibull2-options SIGMA=EST and C=EST. Agreement between the reference line and the point pattern indicates that the Weibull distribution with parameters
with the Weibull2-options SIGMA=EST and C=EST. Agreement between the reference line and the point pattern indicates that the Weibull distribution with parameters 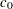 ,
,  , and
, and  is a good fit. You can specify the SCALE= Weibull2-option as an alias for the SIGMA= Weibull2-option and the SHAPE= Weibull2-option as an alias for the C= Weibull2-option. See Example 4.34.
is a good fit. You can specify the SCALE= Weibull2-option as an alias for the SIGMA= Weibull2-option and the SHAPE= Weibull2-option as an alias for the C= Weibull2-option. See Example 4.34. - † WGRID=n
-
specifies the line thickness for the grid when producing traditional graphics. The option does not apply to ODS Graphics output.
- ZETA=value | EST
specifies a value for the scale parameter
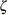 for the lognormal quantile plots requested with the LOGNORMAL option. Enclose the ZETA= lognormal-option in parentheses after the LOGNORMAL option. To request a distribution reference line with intercept
for the lognormal quantile plots requested with the LOGNORMAL option. Enclose the ZETA= lognormal-option in parentheses after the LOGNORMAL option. To request a distribution reference line with intercept  and slope
and slope  , specify the THETA=
, specify the THETA= and ZETA=
and ZETA=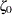 .
.
 terminates
terminates 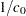 )
) 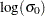 )
)