The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing Values Rounding Descriptive Statistics Calculating the Mode Calculating Percentiles Tests for Location Confidence Limits for Parameters of the Normal Distribution Robust Estimators Creating Line Printer Plots Creating High-Resolution Graphics Using the CLASS Statement to Create Comparative Plots Positioning Insets Formulas for Fitted Continuous Distributions Goodness-of-Fit Tests Kernel Density Estimates Construction of Quantile-Quantile and Probability Plots Interpretation of Quantile-Quantile and Probability Plots Distributions for Probability and Q-Q Plots Estimating Shape Parameters Using Q-Q Plots Estimating Location and Scale Parameters Using Q-Q Plots Estimating Percentiles Using Q-Q Plots Input Data Sets OUT= Output Data Set in the OUTPUT Statement OUTHISTOGRAM= Output Data Set OUTKERNEL= Output Data Set OUTTABLE= Output Data Set Tables for Summary Statistics ODS Table Names ODS Tables for Fitted Distributions ODS Graphics Computational Resources
Missing Values Rounding Descriptive Statistics Calculating the Mode Calculating Percentiles Tests for Location Confidence Limits for Parameters of the Normal Distribution Robust Estimators Creating Line Printer Plots Creating High-Resolution Graphics Using the CLASS Statement to Create Comparative Plots Positioning Insets Formulas for Fitted Continuous Distributions Goodness-of-Fit Tests Kernel Density Estimates Construction of Quantile-Quantile and Probability Plots Interpretation of Quantile-Quantile and Probability Plots Distributions for Probability and Q-Q Plots Estimating Shape Parameters Using Q-Q Plots Estimating Location and Scale Parameters Using Q-Q Plots Estimating Percentiles Using Q-Q Plots Input Data Sets OUT= Output Data Set in the OUTPUT Statement OUTHISTOGRAM= Output Data Set OUTKERNEL= Output Data Set OUTTABLE= Output Data Set Tables for Summary Statistics ODS Table Names ODS Tables for Fitted Distributions ODS Graphics Computational Resources -
Examples
 Computing Descriptive Statistics for Multiple Variables Calculating Modes Identifying Extreme Observations and Extreme Values Creating a Frequency Table Creating Plots for Line Printer Output Analyzing a Data Set With a FREQ Variable Saving Summary Statistics in an OUT= Output Data Set Saving Percentiles in an Output Data Set Computing Confidence Limits for the Mean, Standard Deviation, and Variance Computing Confidence Limits for Quantiles and Percentiles Computing Robust Estimates Testing for Location Performing a Sign Test Using Paired Data Creating a Histogram Creating a One-Way Comparative Histogram Creating a Two-Way Comparative Histogram Adding Insets with Descriptive Statistics Binning a Histogram Adding a Normal Curve to a Histogram Adding Fitted Normal Curves to a Comparative Histogram Fitting a Beta Curve Fitting Lognormal, Weibull, and Gamma Curves Computing Kernel Density Estimates Fitting a Three-Parameter Lognormal Curve Annotating a Folded Normal Curve Creating Lognormal Probability Plots Creating a Histogram to Display Lognormal Fit Creating a Normal Quantile Plot Adding a Distribution Reference Line Interpreting a Normal Quantile Plot Estimating Three Parameters from Lognormal Quantile Plots Estimating Percentiles from Lognormal Quantile Plots Estimating Parameters from Lognormal Quantile Plots Comparing Weibull Quantile Plots Creating a Cumulative Distribution Plot Creating a P-P Plot
Computing Descriptive Statistics for Multiple Variables Calculating Modes Identifying Extreme Observations and Extreme Values Creating a Frequency Table Creating Plots for Line Printer Output Analyzing a Data Set With a FREQ Variable Saving Summary Statistics in an OUT= Output Data Set Saving Percentiles in an Output Data Set Computing Confidence Limits for the Mean, Standard Deviation, and Variance Computing Confidence Limits for Quantiles and Percentiles Computing Robust Estimates Testing for Location Performing a Sign Test Using Paired Data Creating a Histogram Creating a One-Way Comparative Histogram Creating a Two-Way Comparative Histogram Adding Insets with Descriptive Statistics Binning a Histogram Adding a Normal Curve to a Histogram Adding Fitted Normal Curves to a Comparative Histogram Fitting a Beta Curve Fitting Lognormal, Weibull, and Gamma Curves Computing Kernel Density Estimates Fitting a Three-Parameter Lognormal Curve Annotating a Folded Normal Curve Creating Lognormal Probability Plots Creating a Histogram to Display Lognormal Fit Creating a Normal Quantile Plot Adding a Distribution Reference Line Interpreting a Normal Quantile Plot Estimating Three Parameters from Lognormal Quantile Plots Estimating Percentiles from Lognormal Quantile Plots Estimating Parameters from Lognormal Quantile Plots Comparing Weibull Quantile Plots Creating a Cumulative Distribution Plot Creating a P-P Plot - References
| OUTTABLE= Output Data Set |
The OUTTABLE= data set saves univariate statistics in a data set that contains one observation per analysis variable. The following variables are saved:
Variable |
Description |
|---|---|
_CSS_ |
corrected sum of squares |
_CV_ |
coefficient of variation |
_GINI_ |
Gini’s mean difference |
_KURT_ |
kurtosis |
_MAD_ |
median absolute difference about the median |
_MAX_ |
maximum |
_MEAN_ |
mean |
_MEDIAN_ |
median |
_MIN_ |
minimum |
_MODE_ |
mode |
_MSIGN_ |
sign statistic |
_NMISS_ |
number of missing observations |
_NOBS_ |
number of nonmissing observations |
_NORMAL_ |
test statistic for normality |
_P1_ |
|
_P5_ |
|
_P10_ |
|
_P90_ |
|
_P95_ |
|
_P99_ |
|
_PROBM_ |
p-value of sign statistic |
_PROBN_ |
p-value of test for normality |
_PROBS_ |
p-value of signed rank test |
_PROBT_ |
p-value of t statistic |
_Q1_ |
|
_Q3_ |
|
_QN_ |
|
_QRANGE_ |
interquartile range (upper quartile minus lower quartile) |
_RANGE_ |
range |
_SGNRNK_ |
centered sign rank |
_SKEW_ |
skewness |
_SN_ |
|
_STD_ |
standard deviation |
_STDGINI_ |
Gini’s standard deviation |
_STDMAD_ |
MAD standard deviation |
_STDMEAN_ |
standard error of the mean |
_STDQN_ |
|
_STDQRANGE_ |
interquartile range standard deviation |
_STDSN_ |
|
_SUMWGT_ |
sum of the weights |
_SUM_ |
sum |
_T_ |
Student’s t statistic |
_USS_ |
uncorrected sum of squares |
_VARI_ |
variance |
_VAR_ |
variable name |
The OUTTABLE= data set and the OUT= data set see the section OUT= Output Data Set in the OUTPUT Statement) contain essentially the same information. in the OUT= data set (see the section OUT= Output Data Set in the OUTPUT Statement). However, the structure of the OUTTABLE= data set may be more appropriate when you are computing summary statistics for more than one analysis variable in the same invocation of the UNIVARIATE procedure. Each observation in the OUTTABLE= data set corresponds to a different analysis variable, and the variables in the data set correspond to summary statistics and indices.
For example, suppose you have 10 analysis variables (P1-P10). The following statements create an OUTTABLE= data set named Table, which contains summary statistics for each of these variables:
data Analysis; input A1-A10; datalines; 72 223 332 138 110 145 23 293 353 458 97 54 61 196 275 171 117 72 81 141 56 170 140 400 371 72 60 20 484 138 124 6 332 493 214 43 125 55 372 30 152 236 222 76 187 126 192 334 109 546 5 260 194 277 176 96 109 184 240 261 161 253 153 300 37 156 282 293 451 299 128 121 254 297 363 132 209 257 429 295 116 152 331 27 442 103 80 393 383 94 43 178 278 159 25 180 253 333 51 225 34 128 182 415 524 112 13 186 145 131 142 236 234 255 211 80 281 135 179 11 108 215 335 66 254 196 190 363 226 379 62 232 219 474 31 139 15 56 429 298 177 218 275 171 457 146 163 18 155 129 0 235 83 239 398 99 226 389 498 18 147 199 324 258 504 2 218 295 422 287 39 161 156 198 214 58 238 19 231 548 120 42 372 420 232 112 157 79 197 166 178 83 238 492 463 68 46 386 45 81 161 267 372 296 501 96 11 288 330 74 14 2 52 81 169 63 194 161 173 54 22 181 92 272 417 94 188 180 367 342 55 248 214 422 133 193 144 318 271 479 56 83 169 30 379 5 296 320 396 597 ;
proc univariate data=Analysis outtable=Table noprint; var A1-A10; run;
The following statements create the table shown in Figure 4.15, which contains the mean, standard deviation, and so on, for each analysis variable:
proc print data=Table label noobs; var _VAR_ _MIN_ _MEAN_ _MAX_ _STD_; label _VAR_='Analysis'; run;
| Test Scores for a College Course |
| Analysis | Minimum | Mean | Maximum | Standard Deviation |
|---|---|---|---|---|
| A1 | 0 | 90.76 | 178 | 57.024 |
| A2 | 2 | 167.32 | 267 | 81.628 |
| A3 | 52 | 224.56 | 372 | 96.525 |
| A4 | 27 | 258.08 | 493 | 145.218 |
| A5 | 25 | 283.48 | 524 | 157.033 |
| A6 | 2 | 107.48 | 196 | 52.437 |
| A7 | 11 | 153.20 | 296 | 90.031 |
| A8 | 18 | 217.08 | 393 | 130.031 |
| A9 | 45 | 280.68 | 498 | 140.943 |
| A10 | 11 | 243.24 | 597 | 178.799 |
 st percentile
st percentile  th percentile
th percentile  th percentile
th percentile  th percentile
th percentile  th percentile
th percentile  th percentile
th percentile  th percentile (lower quartile)
th percentile (lower quartile)  th percentile (upper quartile)
th percentile (upper quartile) 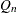
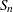 (see
(see