The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing Values Rounding Descriptive Statistics Calculating the Mode Calculating Percentiles Tests for Location Confidence Limits for Parameters of the Normal Distribution Robust Estimators Creating Line Printer Plots Creating High-Resolution Graphics Using the CLASS Statement to Create Comparative Plots Positioning Insets Formulas for Fitted Continuous Distributions Goodness-of-Fit Tests Kernel Density Estimates Construction of Quantile-Quantile and Probability Plots Interpretation of Quantile-Quantile and Probability Plots Distributions for Probability and Q-Q Plots Estimating Shape Parameters Using Q-Q Plots Estimating Location and Scale Parameters Using Q-Q Plots Estimating Percentiles Using Q-Q Plots Input Data Sets OUT= Output Data Set in the OUTPUT Statement OUTHISTOGRAM= Output Data Set OUTKERNEL= Output Data Set OUTTABLE= Output Data Set Tables for Summary Statistics ODS Table Names ODS Tables for Fitted Distributions ODS Graphics Computational Resources
Missing Values Rounding Descriptive Statistics Calculating the Mode Calculating Percentiles Tests for Location Confidence Limits for Parameters of the Normal Distribution Robust Estimators Creating Line Printer Plots Creating High-Resolution Graphics Using the CLASS Statement to Create Comparative Plots Positioning Insets Formulas for Fitted Continuous Distributions Goodness-of-Fit Tests Kernel Density Estimates Construction of Quantile-Quantile and Probability Plots Interpretation of Quantile-Quantile and Probability Plots Distributions for Probability and Q-Q Plots Estimating Shape Parameters Using Q-Q Plots Estimating Location and Scale Parameters Using Q-Q Plots Estimating Percentiles Using Q-Q Plots Input Data Sets OUT= Output Data Set in the OUTPUT Statement OUTHISTOGRAM= Output Data Set OUTKERNEL= Output Data Set OUTTABLE= Output Data Set Tables for Summary Statistics ODS Table Names ODS Tables for Fitted Distributions ODS Graphics Computational Resources -
Examples
 Computing Descriptive Statistics for Multiple Variables Calculating Modes Identifying Extreme Observations and Extreme Values Creating a Frequency Table Creating Plots for Line Printer Output Analyzing a Data Set With a FREQ Variable Saving Summary Statistics in an OUT= Output Data Set Saving Percentiles in an Output Data Set Computing Confidence Limits for the Mean, Standard Deviation, and Variance Computing Confidence Limits for Quantiles and Percentiles Computing Robust Estimates Testing for Location Performing a Sign Test Using Paired Data Creating a Histogram Creating a One-Way Comparative Histogram Creating a Two-Way Comparative Histogram Adding Insets with Descriptive Statistics Binning a Histogram Adding a Normal Curve to a Histogram Adding Fitted Normal Curves to a Comparative Histogram Fitting a Beta Curve Fitting Lognormal, Weibull, and Gamma Curves Computing Kernel Density Estimates Fitting a Three-Parameter Lognormal Curve Annotating a Folded Normal Curve Creating Lognormal Probability Plots Creating a Histogram to Display Lognormal Fit Creating a Normal Quantile Plot Adding a Distribution Reference Line Interpreting a Normal Quantile Plot Estimating Three Parameters from Lognormal Quantile Plots Estimating Percentiles from Lognormal Quantile Plots Estimating Parameters from Lognormal Quantile Plots Comparing Weibull Quantile Plots Creating a Cumulative Distribution Plot Creating a P-P Plot
Computing Descriptive Statistics for Multiple Variables Calculating Modes Identifying Extreme Observations and Extreme Values Creating a Frequency Table Creating Plots for Line Printer Output Analyzing a Data Set With a FREQ Variable Saving Summary Statistics in an OUT= Output Data Set Saving Percentiles in an Output Data Set Computing Confidence Limits for the Mean, Standard Deviation, and Variance Computing Confidence Limits for Quantiles and Percentiles Computing Robust Estimates Testing for Location Performing a Sign Test Using Paired Data Creating a Histogram Creating a One-Way Comparative Histogram Creating a Two-Way Comparative Histogram Adding Insets with Descriptive Statistics Binning a Histogram Adding a Normal Curve to a Histogram Adding Fitted Normal Curves to a Comparative Histogram Fitting a Beta Curve Fitting Lognormal, Weibull, and Gamma Curves Computing Kernel Density Estimates Fitting a Three-Parameter Lognormal Curve Annotating a Folded Normal Curve Creating Lognormal Probability Plots Creating a Histogram to Display Lognormal Fit Creating a Normal Quantile Plot Adding a Distribution Reference Line Interpreting a Normal Quantile Plot Estimating Three Parameters from Lognormal Quantile Plots Estimating Percentiles from Lognormal Quantile Plots Estimating Parameters from Lognormal Quantile Plots Comparing Weibull Quantile Plots Creating a Cumulative Distribution Plot Creating a P-P Plot - References
Example 4.24 Fitting a Three-Parameter Lognormal Curve
If you request a lognormal fit with the LOGNORMAL primary option, a two-parameter lognormal distribution is assumed. This means that the shape parameter  and the scale parameter
and the scale parameter 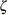 are unknown (unless specified) and that the threshold
are unknown (unless specified) and that the threshold  is known (it is either specified with the THETA= option or assumed to be zero).
is known (it is either specified with the THETA= option or assumed to be zero).
If it is necessary to estimate  in addition to
in addition to 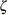 and
and  , the distribution is referred to as a three-parameter lognormal distribution. This example shows how you can request a three-parameter lognormal distribution.
, the distribution is referred to as a three-parameter lognormal distribution. This example shows how you can request a three-parameter lognormal distribution.
A manufacturing process produces a plastic laminate whose strength must exceed a minimum of 25 pounds per square inch (psi). Samples are tested, and a lognormal distribution is observed for the strengths. It is important to estimate  to determine whether the process meets the strength requirement. The following statements save the strengths for 49 samples in the data set Plastic:
to determine whether the process meets the strength requirement. The following statements save the strengths for 49 samples in the data set Plastic:
data Plastic; label Strength = 'Strength in psi'; input Strength @@; datalines; 30.26 31.23 71.96 47.39 33.93 76.15 42.21 81.37 78.48 72.65 61.63 34.90 24.83 68.93 43.27 41.76 57.24 23.80 34.03 33.38 21.87 31.29 32.48 51.54 44.06 42.66 47.98 33.73 25.80 29.95 60.89 55.33 39.44 34.50 73.51 43.41 54.67 99.43 50.76 48.81 31.86 33.88 35.57 60.41 54.92 35.66 59.30 41.96 45.32 ;
The following statements use the LOGNORMAL primary option in the HISTOGRAM statement to display the fitted three-parameter lognormal curve shown in Output 4.24.1:
title 'Three-Parameter Lognormal Fit'; ods graphics off; proc univariate data=Plastic noprint; histogram Strength / lognormal(fill theta = est noprint); inset lognormal / format=6.2 pos=ne; run;
The NOPRINT option suppresses the tables of statistical output produced by default. Specifying THETA=EST requests a local maximum likelihood estimate (LMLE) for  , as described by Cohen (1951). This estimate is then used to compute maximum likelihood estimates for
, as described by Cohen (1951). This estimate is then used to compute maximum likelihood estimates for  and
and 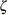 .
.
Note: You can also specify THETA=EST with the WEIBULL primary option to fit a three-parameter Weibull distribution.
A sample program for this example, uniex14.sas, is available in the SAS Sample Library for Base SAS software.