The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
Given a multivariate time series, the VARMAX procedure estimates the model parameters and generates forecasts associated with vector autoregressive moving-average processes with exogenous regressors (VARMAX) models. Often, economic or financial variables are not only contemporaneously correlated to each other, they are also correlated to each other’s past values. The VARMAX procedure can be used to model these types of time relationships. In many economic and financial applications, the variables of interest (dependent, response, or endogenous variables) are influenced by variables external to the system under consideration (independent, input, predictor, regressor, or exogenous variables). The VARMAX procedure enables you to model the dynamic relationship both between the dependent variables and also between the dependent and independent variables.
VARMAX models are defined in terms of the orders of the autoregressive or moving-average process (or both). When you use the VARMAX procedure, these orders can be specified by options or they can be automatically determined. Criteria for automatically determining these orders include the following:
-
Akaike information criterion (AIC)
-
corrected AIC (AICC)
-
Hannan-Quinn (HQ) criterion
-
final prediction error (FPE)
-
Schwarz Bayesian criterion (SBC), also known as Bayesian information criterion (BIC)
If you do not want to use the automatic order selection, the VARMAX procedure provides autoregressive order identification aids:
-
partial cross-correlations
-
Yule-Walker estimates
-
partial autoregressive coefficients
-
partial canonical correlations
For situations where the stationarity of the time series is in question, the VARMAX procedure provides tests to aid in determining the presence of unit roots and cointegration. These tests include the following:
-
Dickey-Fuller tests
-
Johansen cointegration test for nonstationary vector processes of integrated order one
-
Stock-Watson common trends test for the possibility of cointegration among nonstationary vector processes of integrated order one
-
Johansen cointegration test for nonstationary vector processes of integrated order two
For stationary vector times series (or nonstationary series made stationary by appropriate differencing), the VARMAX procedure provides for vector autoregressive and moving-average (VARMA) and Bayesian vector autoregressive (BVAR) models. To cope with the problem of high dimensionality in the parameters of the VAR model, the VARMAX procedure provides both vector error correction model (VECM) and Bayesian vector error correction model (BVECM). Bayesian models are used when prior information about the model parameters is available. The VARMAX procedure also allows independent (exogenous) variables with their distributed lags to influence dependent (endogenous) variables in various models such as VARMAX, BVARX, VECMX, and BVECMX models.
Forecasting is one of the main objectives of multivariate time series analysis. After successfully fitting the VARMAX, BVARX, VECMX, and BVECMX models, the VARMAX procedure computes predicted values based on the parameter estimates and the past values of the vector time series.
The model parameter estimation methods are the following:
-
least squares (LS)
-
maximum likelihood (ML)
The VARMAX procedure provides various hypothesis tests of long-run effects and adjustment coefficients by using the likelihood ratio test based on Johansen cointegration analysis. The VARMAX procedure offers the likelihood ratio test of the weak exogeneity for each variable.
After fitting the model parameters, the VARMAX procedure provides for model checks and residual analysis by using the following tests:
-
Durbin-Watson (DW) statistics
-
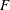 test for autoregressive conditional heteroscedastic (ARCH) disturbance
test for autoregressive conditional heteroscedastic (ARCH) disturbance
-
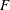 test for AR disturbance
test for AR disturbance
-
Jarque-Bera normality test
-
Portmanteau test
The VARMAX procedure supports several modeling features, including the following:
-
seasonal deterministic terms
-
subset models
-
multiple regression with distributed lags
-
dead-start model that does not have present values of the exogenous variables
-
GARCH-type multivariate conditional heteroscedasticity models
The VARMAX procedure provides a Granger causality test to determine the Granger-causal relationships between two distinct groups of variables. It also provides the following:
-
infinite order AR representation
-
impulse response function (or infinite order MA representation)
-
decomposition of the predicted error covariances
-
roots of the characteristic functions for both the AR and MA parts to evaluate the proximity of the roots to the unit circle
-
contemporaneous relationships among the components of the vector time series