The VARMAX Procedure

Parameter Estimation and Testing on Restrictions

In the previous example, the VARX(1,0) model is written as

$\begin{eqnarray*} \mb{y} _{t} = \bdelta + \Theta ^{*}_0\mb{x} _{t} + \Phi _1\mb{y} _{t-1} + \bepsilon _ t \end{eqnarray*}$

with

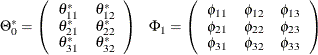
$\begin{eqnarray*} \Theta _0^{*} = \left( \begin{array}{rr} \theta ^{*}_{11} & \theta ^{*}_{12} \\ \theta ^{*}_{21} & \theta ^{*}_{22} \\ \theta ^{*}_{31} & \theta ^{*}_{32} \end{array} \right) ~ ~ ~ \Phi _1 = \left( \begin{array}{rrr} \phi _{11} & \phi _{12} & \phi _{13} \\ \phi _{21} & \phi _{22} & \phi _{23} \\ \phi _{31} & \phi _{32} & \phi _{33} \end{array} \right) \end{eqnarray*}$

In Figure 35.20 of the preceding section, you can see several insignificant parameters. For example, the coefficients XL0_1_2, AR1_1_2, and AR1_3_2 are insignificant.

The following statements restrict the coefficients of $\theta _{12}^*=\phi _{12}=\phi _{32}=0$ for the VARX(1,0) model.

/*--- Models with Restrictions and Tests ---*/

proc varmax data=grunfeld;
   model y1-y3 = x1 x2 / p=1 print=(estimates);
   restrict XL(0,1,2)=0, AR(1,1,2)=0, AR(1,3,2)=0;
run;

The output in Figure 35.21 shows that three parameters $\theta _{12}^*$ , $\phi _{12}$ , and $\phi _{32}$ are replaced by the restricted values, zeros. In the schematic representation of parameter estimates, the three restricted parameters $\theta _{12}^*$ , $\phi _{12}$ , and $\phi _{32}$ are replaced by $*$ .

Figure 35.21: Parameter Estimation with Restrictions

The VARMAX Procedure

XLag
Lag	Variable	x1	x2
0	y1	1.67592	0.00000
	y2	-6.30880	2.65308
	y3	-0.03576	-0.00919

AR
Lag	Variable	y1	y2	y3
1	y1	0.27671	0.00000	0.01747
	y2	-2.16968	0.10945	-0.93053
	y3	0.96398	0.00000	0.93412

Schematic Representation
Variable/Lag	C	XL0	AR1
y1	.	+*	...
y2	+	.+	..-
y3	-	..	+*+
+ is > 2std error, - is < -2std error, . is between, * is N/A

The output in Figure 35.22 shows the estimates of the Lagrangian parameters and their significance. Based on the p-values associated with the Lagrangian parameters, you cannot reject the null hypotheses $\theta _{12}^*=0$ , $\phi _{12}=0$ , and $\phi _{32}=0$ with the 0.05 significance level.

Figure 35.22: RESTRICT Statement Results

Testing of the Restricted Parameters
Parameter	Estimate	Standard Error	t Value	Pr > \|t\|	Equation
Restrict0	1.74969	21.44026	0.08	0.9389	XL0_1_2 = 0
Restrict1	30.36254	70.74347	0.43	0.6899	AR1_1_2 = 0
Restrict2	55.42191	164.03075	0.34	0.7524	AR1_3_2 = 0

The TEST statement in the following example tests $\phi _{31}=0$ and $\theta _{12}^*=\phi _{12}=\phi _{32}=0$ for the VARX(1,0) model:

proc varmax data=grunfeld;
   model y1-y3 = x1 x2 / p=1;
   test AR(1,3,1)=0;
   test XL(0,1,2)=0, AR(1,1,2)=0, AR(1,3,2)=0;
run;

The output in Figure 35.23 shows that the first column in the output is the index corresponding to each TEST statement. You can reject the hypothesis test $\phi _{31}=0$ at the 0.05 significance level, but you cannot reject the joint hypothesis test $\theta _{12}^*=\phi _{12}=\phi _{32}=0$ at the 0.05 significance level.

Figure 35.23: TEST Statement Results

The VARMAX Procedure

Testing of the Parameters
Test	DF	Chi-Square	Pr > ChiSq
1	1	150.31	<.0001
2	3	0.34	0.9522