The VARMAX Procedure

Vector Error Correction Model

Subsections:

Example of Vector Error Correction Model
Cointegration Testing

A vector error correction model (VECM) can lead to a better understanding of the nature of any nonstationarity among the different component series and can also improve longer term forecasting over an unconstrained model.

The VECM(p) form with the cointegration rank $r(\leq k)$ is written as

$\begin{eqnarray*} \Delta \mb{y} _{t} = \bdelta + \Pi \mb{y} _{t-1} + \sum _{i=1}^{p-1}\Phi ^*_ i \Delta \mb{y} _{t-i} + \bepsilon _ t \end{eqnarray*}$

where $\Delta$ is the differencing operator, such that $\Delta \mb{y} _{t} = \mb{y} _{t}-\mb{y} _{t-1}$ ; $\Pi = \alpha \beta ’$ , where $\alpha$ and $\beta$ are $k\times r$ matrices; $\Phi ^*_ i$ is a $k\times k$ matrix.

It has an equivalent VAR(p) representation as described in the preceding section.

$\begin{eqnarray*} \mb{y} _{t} = \bdelta + (I_ k+\Pi +\Phi ^*_1) \mb{y} _{t-1} +\sum _{i=2}^{p-1} (\Phi ^*_ i-\Phi ^*_{i-1}) \mb{y} _{t-i} -\Phi ^*_{p-1}\mb{y} _{t-p} + \bepsilon _ t \end{eqnarray*}$

where $I_ k$ is a $k\times k$ identity matrix.

Example of Vector Error Correction Model

An example of the second-order nonstationary vector autoregressive model is

$\begin{eqnarray*} \mb{y} _ t = \left( \begin{array}{rr} -0.2 & 0.1 \\ 0.5 & 0.2 \\ \end{array} \right) \mb{y} _{t-1} + \left( \begin{array}{rr} 0.8 & 0.7 \\ -0.4 & 0.6 \\ \end{array} \right) \mb{y} _{t-2} + \bepsilon _ t \end{eqnarray*}$

with

$\begin{eqnarray*} \Sigma = \left( \begin{array}{rr} 100 & 0 \\ 0 & 100 \\ \end{array} \right) ~ ~ \mr{and} ~ ~ \mb{y} _0 = \left( \begin{array}{r} 0 \\ 0 \\ \end{array} \right) \end{eqnarray*}$

This process can be given the following VECM(2) representation with the cointegration rank one:

$\begin{eqnarray*} \Delta \mb{y} _ t = \left( \begin{array}{r} -0.4 \\ 0.1 \\ \end{array} \right) ( 1, -2 ) \mb{y} _{t-1} - \left( \begin{array}{rr} 0.8 & 0.7 \\ -0.4 & 0.6 \\ \end{array} \right) \Delta \mb{y} _{t-1} + \bepsilon _ t \end{eqnarray*}$

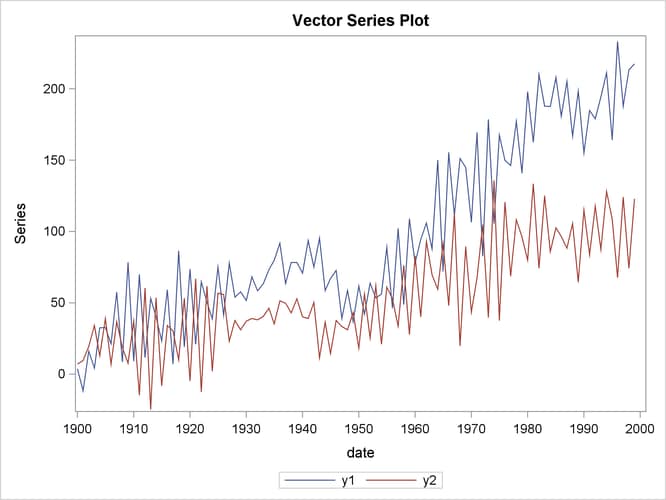
The following PROC IML statements generate simulated data for the VECM(2) form specified above and plot the data as shown in Figure 35.12:

proc iml;
   sig = 100*i(2);
   phi = {-0.2 0.1, 0.5 0.2, 0.8 0.7, -0.4 0.6};
   call varmasim(y,phi) sigma=sig n=100 initial=0
                        seed=45876;
   cn = {'y1' 'y2'};
   create simul2 from y[colname=cn];
   append from y;
quit;

data simul2;
   set simul2;
   date = intnx( 'year', '01jan1900'd, _n_-1 );
   format date year4. ;
run;

proc timeseries data=simul2 vectorplot=series;
   id date interval=year;
   var y1 y2;
run;

Figure 35.12: Plot of Generated Data Process

Cointegration Testing

The following statements use the Johansen cointegration rank test. The COINTTEST=(JOHANSEN) option does the Johansen trace test and is equivalent to specifying COINTTEST with no additional options or the COINTTEST=(JOHANSEN=(TYPE=TRACE)) option.

/*--- Cointegration Test ---*/

proc varmax data=simul2;
   model y1 y2 / p=2 noint dftest cointtest=(johansen);
run;

Figure 35.13 shows the output for Dickey-Fuller tests for the nonstationarity of each series and Johansen cointegration rank test between series.

Figure 35.13: Dickey-Fuller Tests and Cointegration Rank Test

The VARMAX Procedure

Unit Root Test
Variable	Type	Rho	Pr < Rho	Tau	Pr < Tau
y1	Zero Mean	1.47	0.9628	1.65	0.9755
	Single Mean	-0.80	0.9016	-0.47	0.8916
	Trend	-10.88	0.3573	-2.20	0.4815
y2	Zero Mean	-0.05	0.6692	-0.03	0.6707
	Single Mean	-6.03	0.3358	-1.72	0.4204
	Trend	-50.49	0.0003	-4.92	0.0006

Cointegration Rank Test Using Trace
H0: Rank=r	H1: Rank>r	Eigenvalue	Trace	Pr > Trace	Drift in ECM	Drift in Process
0	0	0.5086	70.7279	<.0001	NOINT	Constant
1	1	0.0111	1.0921	0.3441

In Dickey-Fuller tests, the second column specifies three types of models, which are zero mean, single mean, or trend. The third column ( Rho ) and the fifth column ( Tau ) are the test statistics for unit root testing. Other columns are their p-values. You can see that both series have unit roots. For a description of Dickey-Fuller tests, see the section PROBDF Function for Dickey-Fuller Tests in Chapter 5: SAS Macros and Functions.

In the cointegration rank test, the last two columns explain the drift in the model or process. Since the NOINT option is specified, the model is

$\begin{eqnarray*} \Delta \mb{y} _{t} = \Pi \mb{y} _{t-1} + \Phi ^*_1 \Delta \mb{y} _{t-1} + \bepsilon _ t \end{eqnarray*}$

The column Drift in ECM indicates that there is no separate drift in the error correction model, and the column Drift in Process indicates that the process has a constant drift before differencing.

H0 is the null hypothesis, and H1 is the alternative hypothesis. The first row tests $r=0$ against $r>0$ ; the second row tests $r=1$ against $r>1$ . The trace test statistics in the fourth column are computed by $-T\sum _{i=r+1}^ k \log (1-\lambda _ i)$ , where $T$ is the available number of observations and $\lambda _ i$ is the eigenvalue in the third column. The p-values for these statistics are output in the fifth column. If you compare the p-value in each row to the significance level of interest, such as 5%, the null hypothesis that there is no cointegrated process (H0: $r=0$ ) is rejected, whereas the null hypothesis that there is at most one cointegrated process (H0: $r=1$ ) cannot be rejected.

The following statements fit a VECM(2) form to the simulated data. From the result in Figure 35.13, the time series are cointegrated with rank = 1. You specify the ECM= option together with the RANK=1 option. For normalizing the value of the cointegrated vector, you specify the normalized variable by using the NORMALIZE= option. The PRINT=(IARR) option provides the VAR(2) representation. The VARMAX procedure output is shown in Figure 35.14 through Figure 35.16.

/*--- Vector Error-Correction Model ---*/

proc varmax data=simul2;
   model y1 y2 / p=2 noint lagmax=3
                 ecm=(rank=1 normalize=y1)
                 print=(iarr estimates);
run;

The ECM= option produces the estimates of the long-run parameter, $\bbeta$ , and the adjustment coefficient, $\balpha$ . In Figure 35.14, "1" indicates the first column of the $\balpha$ and $\bbeta$ matrices. Since the cointegration rank is 1 in the bivariate system, $\balpha$ and $\bbeta$ are two-dimensional vectors. The estimated cointegrating vector is $\hat{\bbeta }=(1, -1.96)’$ . Therefore, the long-run relationship between $y_{1t}$ and $y_{2t}$ is $y_{1t}=1.96y_{2t}$ . The first element of $\hat{\bbeta }$ is 1 since $y_1$ is specified as the normalized variable.

Figure 35.14: Parameter Estimates for the VECM(2) Form

The VARMAX Procedure

Type of Model	VECM(2)
Estimation Method	Maximum Likelihood Estimation
Cointegrated Rank	1

Beta
Variable	1
y1	1.00000
y2	-1.95575

Alpha
Variable	1
y1	-0.46680
y2	0.10667

Figure 35.15 shows the parameter estimates in terms of lag one coefficients, $\mb{y} _{t-1}$ , and lag one first differenced coefficients, $\Delta \mb{y} _{t-1}$ , and their significance. "Alpha * Beta $’$ " indicates the coefficients of $\mb{y} _{t-1}$ and is obtained by multiplying the "Alpha" and "Beta" estimates in Figure 35.14. The parameter AR1 $\_ i\_ j$ corresponds to the elements in the "Alpha * Beta $’$ " matrix. The t values and p-values corresponding to the parameters AR1 $\_ i\_ j$ are missing since the parameters AR1 $\_ i\_ j$ have non-Gaussian distributions. The parameter AR2 $\_ i\_ j$ corresponds to the elements in the differenced lagged AR coefficient matrix. The "D_" prefixed to a variable name in Figure 35.15 implies differencing.

Figure 35.15: Parameter Estimates for the VECM(2) Form

Parameter Alpha * Beta' Estimates
Variable	y1	y2
y1	-0.46680	0.91295
y2	0.10667	-0.20862

AR Coefficients of Differenced Lag
DIF Lag	Variable	y1	y2
1	y1	-0.74332	-0.74621
	y2	0.40493	-0.57157

Model Parameter Estimates
Equation	Parameter	Estimate	Standard Error	t Value	Pr > \|t\|	Variable
D_y1	AR1_1_1	-0.46680	0.04786			y1(t-1)
	AR1_1_2	0.91295	0.09359			y2(t-1)
	AR2_1_1	-0.74332	0.04526	-16.42	0.0001	D_y1(t-1)
	AR2_1_2	-0.74621	0.04769	-15.65	0.0001	D_y2(t-1)
D_y2	AR1_2_1	0.10667	0.05146			y1(t-1)
	AR1_2_2	-0.20862	0.10064			y2(t-1)
	AR2_2_1	0.40493	0.04867	8.32	0.0001	D_y1(t-1)
	AR2_2_2	-0.57157	0.05128	-11.15	0.0001	D_y2(t-1)

The fitted model is given as

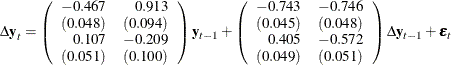
$\begin{eqnarray*} {\Delta \mb{y} }_ t = \left( \begin{array}{rr} -0.467 & 0.913 \\ (0.048) & (0.094)\\ 0.107 & -0.209 \\ (0.051) & (0.100)\\ \end{array} \right) \mb{y} _{t-1} + \left( \begin{array}{rr} -0.743 & -0.746 \\ (0.045)& (0.048) \\ 0.405 & -0.572 \\ (0.049) & (0.051)\\ \end{array} \right) \Delta \mb{y} _{t-1} + \bepsilon _ t \end{eqnarray*}$

Figure 35.16: Change the VECM(2) Form to the VAR(2) Model

Infinite Order AR Representation
Lag	Variable	y1	y2
1	y1	-0.21013	0.16674
	y2	0.51160	0.21980
2	y1	0.74332	0.74621
	y2	-0.40493	0.57157
3	y1	0.00000	0.00000
	y2	0.00000	0.00000

The PRINT=(IARR) option in the previous SAS statements prints the reparameterized coefficient estimates. For the LAGMAX=3 in the SAS statements, the coefficient matrix of lag 3 is zero.

The VECM(2) form in Figure 35.16 can be rewritten as the following second-order vector autoregressive model:

$\begin{eqnarray*} \mb{y} _ t = \left( \begin{array}{rr} -0.210 & 0.167 \\ 0.512 & 0.220 \end{array} \right) \mb{y} _{t-1} + \left( \begin{array}{rr} 0.743 & 0.746 \\ -0.405 & 0.572 \end{array} \right) \mb{y} _{t-2} + \bepsilon _ t \end{eqnarray*}$