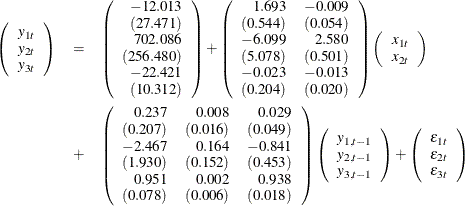The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
A VAR process can be affected by other observable variables that are determined outside the system of interest. Such variables are called exogenous (independent) variables. Exogenous variables can be stochastic or nonstochastic. The process can also be affected by the lags of exogenous variables. A model used to describe this process is called a VARX(p,s) model.
The VARX(p,s) model is written as
where ![]() is an r-dimensional time series vector and
is an r-dimensional time series vector and ![]() is a
is a ![]() matrix.
matrix.
For example, a VARX(1,0) model is
where ![]() and
and ![]() .
.
The following statements fit the VARX(1,0) model to the given data:
data grunfeld;
input year y1 y2 y3 x1 x2 x3;
label y1='Gross Investment GE'
y2='Capital Stock Lagged GE'
y3='Value of Outstanding Shares GE Lagged'
x1='Gross Investment W'
x2='Capital Stock Lagged W'
x3='Value of Outstanding Shares Lagged W';
datalines;
1935 33.1 1170.6 97.8 12.93 191.5 1.8
1936 45.0 2015.8 104.4 25.90 516.0 .8
1937 77.2 2803.3 118.0 35.05 729.0 7.4
1938 44.6 2039.7 156.2 22.89 560.4 18.1
... more lines ...
/*--- Vector Autoregressive Process with Exogenous Variables ---*/
proc varmax data=grunfeld;
model y1-y3 = x1 x2 / p=1 lagmax=5
printform=univariate
print=(impulsx=(all) estimates);
run;
The VARMAX procedure output is shown in Figure 35.18 through Figure 35.20.
Figure 35.18 shows the descriptive statistics for the dependent (endogenous) and independent (exogenous) variables with labels.
Figure 35.18: Descriptive Statistics for the VARX(1, 0) Model
| Number of Observations | 20 |
|---|---|
| Number of Pairwise Missing | 0 |
| Simple Summary Statistics | |||||||
|---|---|---|---|---|---|---|---|
| Variable | Type | N | Mean | Standard Deviation |
Min | Max | Label |
| y1 | Dependent | 20 | 102.29000 | 48.58450 | 33.10000 | 189.60000 | Gross Investment GE |
| y2 | Dependent | 20 | 1941.32500 | 413.84329 | 1170.60000 | 2803.30000 | Capital Stock Lagged GE |
| y3 | Dependent | 20 | 400.16000 | 250.61885 | 97.80000 | 888.90000 | Value of Outstanding Shares GE Lagged |
| x1 | Independent | 20 | 42.89150 | 19.11019 | 12.93000 | 90.08000 | Gross Investment W |
| x2 | Independent | 20 | 670.91000 | 222.39193 | 191.50000 | 1193.50000 | Capital Stock Lagged W |
Figure 35.19 shows the parameter estimates for the constant, the lag zero coefficients of exogenous variables, and the lag one AR coefficients. From the schematic representation of parameter estimates, the significance of the parameter estimates can be easily verified. The symbol "C" means the constant and "XL0" means the lag zero coefficients of exogenous variables.
Figure 35.19: Parameter Estimates for the VARX(1, 0) Model
| Type of Model | VARX(1,0) |
|---|---|
| Estimation Method | Least Squares Estimation |
| Constant | |
|---|---|
| Variable | Constant |
| y1 | -12.01279 |
| y2 | 702.08673 |
| y3 | -22.42110 |
| XLag | |||
|---|---|---|---|
| Lag | Variable | x1 | x2 |
| 0 | y1 | 1.69281 | -0.00859 |
| y2 | -6.09850 | 2.57980 | |
| y3 | -0.02317 | -0.01274 | |
| AR | ||||
|---|---|---|---|---|
| Lag | Variable | y1 | y2 | y3 |
| 1 | y1 | 0.23699 | 0.00763 | 0.02941 |
| y2 | -2.46656 | 0.16379 | -0.84090 | |
| y3 | 0.95116 | 0.00224 | 0.93801 | |
| Schematic Representation | |||
|---|---|---|---|
| Variable/Lag | C | XL0 | AR1 |
| y1 | . | +. | ... |
| y2 | + | .+ | ... |
| y3 | - | .. | +.+ |
| + is > 2*std error, - is < -2*std error, . is between, * is N/A | |||
Figure 35.20 shows the parameter estimates and their significance.
Figure 35.20: Parameter Estimates for the VARX(1, 0) Model Continued
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| y1 | CONST1 | -12.01279 | 27.47108 | -0.44 | 0.6691 | 1 |
| XL0_1_1 | 1.69281 | 0.54395 | 3.11 | 0.0083 | x1(t) | |
| XL0_1_2 | -0.00859 | 0.05361 | -0.16 | 0.8752 | x2(t) | |
| AR1_1_1 | 0.23699 | 0.20668 | 1.15 | 0.2722 | y1(t-1) | |
| AR1_1_2 | 0.00763 | 0.01627 | 0.47 | 0.6470 | y2(t-1) | |
| AR1_1_3 | 0.02941 | 0.04852 | 0.61 | 0.5548 | y3(t-1) | |
| y2 | CONST2 | 702.08673 | 256.48046 | 2.74 | 0.0169 | 1 |
| XL0_2_1 | -6.09850 | 5.07849 | -1.20 | 0.2512 | x1(t) | |
| XL0_2_2 | 2.57980 | 0.50056 | 5.15 | 0.0002 | x2(t) | |
| AR1_2_1 | -2.46656 | 1.92967 | -1.28 | 0.2235 | y1(t-1) | |
| AR1_2_2 | 0.16379 | 0.15193 | 1.08 | 0.3006 | y2(t-1) | |
| AR1_2_3 | -0.84090 | 0.45304 | -1.86 | 0.0862 | y3(t-1) | |
| y3 | CONST3 | -22.42110 | 10.31166 | -2.17 | 0.0487 | 1 |
| XL0_3_1 | -0.02317 | 0.20418 | -0.11 | 0.9114 | x1(t) | |
| XL0_3_2 | -0.01274 | 0.02012 | -0.63 | 0.5377 | x2(t) | |
| AR1_3_1 | 0.95116 | 0.07758 | 12.26 | 0.0001 | y1(t-1) | |
| AR1_3_2 | 0.00224 | 0.00611 | 0.37 | 0.7201 | y2(t-1) | |
| AR1_3_3 | 0.93801 | 0.01821 | 51.50 | 0.0001 | y3(t-1) | |
The fitted model is given as