Multivariate GARCH Modeling :: SAS/ETS(R) 13.2 User's Guide

BEKK Representation

Engle and Kroner (1995) propose a general multivariate GARCH model and call it a BEKK representation. Let $\mathcal{F}(t-1)$ be the sigma field generated by the past values of $\bepsilon _ t$ , and let $H_ t$ be the conditional covariance matrix of the k-dimensional random vector $\bepsilon _ t$ . Let $H_ t$ be measurable with respect to $\mathcal{F}(t-1)$ ; then the multivariate GARCH model can be written as

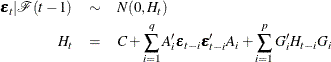
$\begin{eqnarray*} \bepsilon _ t|\mathcal{F}(t-1) & \sim & N(0,H_ t) \\ H_ t & = & C + \sum _{i=1}^ q A_{i}’ \bepsilon _{t-i} \bepsilon _{t-i}’A_{i} + \sum _{i=1}^ p G_{i}’H_{t-i}G_{i} \end{eqnarray*}$

where C, $A_{i}$ and $G_{i}$ are $k\times k$ parameter matrices.

Consider the bivariate GARCH(1,1) model

$\begin{eqnarray*} H_ t & =& \left[ \begin{array}{cc} c_{11} & c_{12} \\ c_{12} & c_{22} \end{array} \right] +\left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]’ \left[ \begin{array}{cc}\epsilon ^2_{1,t-1} & \epsilon _{1,t-1}\epsilon _{2,t-1} \\ \epsilon _{2,t-1}\epsilon _{1,t-1} & \epsilon ^2_{2,t-1} \end{array} \right] \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] \\ & & + \left[ \begin{array}{cc} g_{11} & g_{12} \\ g_{21} & g_{22} \end{array} \right]’ H_{t-1}\left[ \begin{array}{cc} g_{11} & g_{12} \\ g_{21} & g_{22} \end{array} \right] \end{eqnarray*}$

or, representing the univariate model,

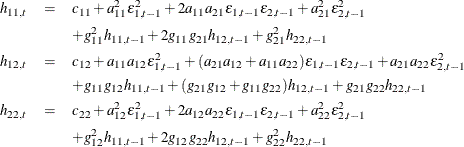
$\begin{eqnarray*} h_{11,t} & =& c_{11} + a_{11}^2\epsilon ^2_{1,t-1} + 2a_{11}a_{21}\epsilon _{1,t-1}\epsilon _{2,t-1} + a_{21}^2\epsilon ^2_{2,t-1} \\ & & + g_{11}^2 h_{11,t-1} + 2g_{11}g_{21}h_{12,t-1} + g_{21}^2h_{22,t-1} \\ h_{12,t} & =& c_{12} + a_{11}a_{12}\epsilon ^2_{1,t-1} + (a_{21}a_{12}+a_{11}a_{22}) \epsilon _{1,t-1}\epsilon _{2,t-1} + a_{21}a_{22}\epsilon ^2_{2,t-1} \\ & & + g_{11}g_{12} h_{11,t-1} + (g_{21}g_{12}+g_{11}g_{22})h_{12,t-1} + g_{21}g_{22}h_{22,t-1}\\ h_{22,t} & =& c_{22} + a_{12}^2\epsilon ^2_{1,t-1} + 2a_{12}a_{22}\epsilon _{1,t-1}\epsilon _{2,t-1} + a_{22}^2\epsilon ^2_{2,t-1} \\ & & + g_{12}^2 h_{11,t-1} + 2g_{12}g_{22}h_{12,t-1} + g_{22}^2h_{22,t-1} \\ \end{eqnarray*}$

For the BEKK representation of the bivariate GARCH(1,1) model, the SAS statements are

model y1 y2;
garch q=1 p=1 form=bekk;

The multistep forecast of the conditional covariance matrix, $H_{t+h|t}, h = 1, 2, \ldots$ , is obtained recursively through the formula

$\begin{eqnarray*} H_{t+h|t} & = & C + \sum _{i=1}^{h-1} A_{i}’ H_{t+h-i|t} A_{i} + \sum _{i=h}^ q A_{i}’ \bepsilon _{t+h-i} \bepsilon _{t+h-i}’ A_{i} + \sum _{i=1}^ p G_{i}’ H_{t+h-i|t} G_{i} \end{eqnarray*}$

where $H_{s|t} = H_ s$ for $s \leq t$ .

CCC Representation

Bollerslev (1990) proposes a multivariate GARCH model with time-varying conditional variances and covariances but constant conditional correlations.

The conditional covariance matrix $H_ t$ consists of

$\begin{eqnarray*} H_ t = D_ t S D_ t \end{eqnarray*}$

where $D_ t$ is a $k \times k$ stochastic diagonal matrix with element $\sigma _{i,t}$ and $S$ is a $k \times k$ time-invariant correlation matrix with the typical element $s_{ij}$ .

The element of $H_ t$ is

$\begin{eqnarray*} h_{ij,t} & =& s_{ij}\sigma _{i,t}\sigma _{j,t} ~ ~ ~ ~ i,j=1,\ldots , k \end{eqnarray*}$

Note that $h_{ii,t}=\sigma _{i,t}^2, i=1,\ldots , k$ .

If you specify CORRCONSTANT=EXPECT, the element $s_{ij}$ of the time-invariant correlation matrix $S$ is

$\begin{eqnarray*} s_{ij} = \frac{1}{T}\sum _{t=1}^{T}{\frac{\bepsilon _{i,t}}{\sqrt {h_{ii,t}}}\frac{\bepsilon _{j,t}}{\sqrt {h_{jj,t}}}} \end{eqnarray*}$

where $T$ is the sample size.

By default, or when you specify SUBFORM=GARCH, $\sigma _{i,t}^2$ follows a univariate GARCH process,

$\begin{eqnarray*} \sigma _{i,t}^2 & =& c_ i + \sum _{l=1}^ q a_{ii,l} \bepsilon ^2_{i,t-l} + \sum _{l=1}^ p g_{ii,l} \sigma _{i,t-1}^2 ~ ~ ~ ~ i=1,\ldots , k \end{eqnarray*}$

As shown in many empirical studies, positive and negative innovations have different impacts on future volatility. There is a long list of variations of univariate GARCH models that consider the asymmetricity. Four typical variations follow:

Exponential GARCH (EGARCH) model (Nelson and Cao, 1992)
Quadratic GARCH (QGARCH) model (Engle and Ng, 1993)
Threshold GARCH (TGARCH) model (Glosten, Jaganathan, and Runkle, 1993; Zakoian, 1994)
Power GARCH (PGARCH) model (Ding, Granger, and Engle, 1993)

For more information about the asymmetric GARCH models, see Engle and Ng (1993). You can choose the type of GARCH model of interest by specifying the SUBFORM= option.

The EGARCH model was proposed by Nelson (1991). Nelson and Cao (1992) argue that the nonnegativity constraints in the GARCH model are too restrictive. The GARCH model, implicitly or explicitly, imposes the nonnegative constraints on the parameters, whereas these parameters have no restrictions in the EGARCH model. In the EGARCH model, the conditional variance is an asymmetric function of lagged disturbances,

$\begin{eqnarray*} {\ln }( \sigma _{i,t}^2) & =& c_ i + \sum _{l=1}^{q} {a_{ii,l}\left(b_{ii,l}\frac{\bepsilon _{i,t-l}}{\sigma _{i,t-l}} +|\frac{\bepsilon _{i,t-l}}{\sigma _{i,t-l}}| -\sqrt {\frac{2}{\pi }}\right)} + \sum _{l=1}^{p}{g_{ii,l}{\ln }( \sigma _{i,t-l}^2)} ~ ~ ~ ~ i=1,\ldots , k\\ \end{eqnarray*}$

In the QGARCH model, the lagged errors’ centers are shifted from zero to some constant values,

$\begin{eqnarray*} \sigma _{i,t}^2 & =& c_ i + \sum _{l=1}^{q}{a_{ii,l} (\bepsilon _{i,t-l} - b_{ii,l})^{2}} + \sum _{l=1}^{p}{g_{ii,l} \sigma _{i,t-1}^2} ~ ~ ~ ~ i=1,\ldots , k\\ \end{eqnarray*}$

In the TGARCH model, each lagged squared error has an extra slope coefficient,

$\begin{eqnarray*} \sigma _{i,t}^2 & =& c_ i + \sum _{l=1}^ q (a_{ii,l}+1_{\bepsilon _{i,t-l}<0} {b}_{ii,l}) \bepsilon ^2_{i,t-l} + \sum _{l=1}^ p {g_{ii,l} \sigma _{i,t-1}^2} ~ ~ ~ ~ i=1,\ldots , k\\ \end{eqnarray*}$

where the indicator function $1_{{\bepsilon }_{i,t}<0}$ is one if ${\bepsilon }_{i,t}<0$ and zero otherwise.

The PGARCH model not only considers the asymmetric effect but also provides a way to model the long memory property in the volatility,

$\begin{eqnarray*} \sigma _{i,t}^{2\lambda _ i} = c_ i + \sum _{l=1}^{q}{ a_{ii,l} (|\bepsilon _{i,t-l}|-b_{ii,l}\bepsilon _{i,t-l})^{2\lambda _ i}} + \sum _{l=1}^ p {g_{ii,l} \sigma _{i,t-1}^{2\lambda _ i}} ~ ~ i=1,\ldots , k\\ \end{eqnarray*}$

where $\lambda _ i > 0$ and $|b_{ii,l}| \leq 1, l = 1, ..., q, i=1,\ldots , k$ .

Note that the implemented TGARCH model is also well known as GJR-GARCH (Glosten, Jaganathan, and Runkle, 1993), which is similar to the threshold GARCH model proposed by Zakoian (1994) but not exactly the same. In Zakoian’s model, the conditional standard deviation is a linear function of the past values of the white noise. Zakoian’s model can be regarded as a special case of the PGARCH model when $\lambda _ i=1/2$ .

The following formulas are recursively implemented to obtain the multistep forecast of conditional error variance $\sigma _{i,t+h|t}^2, i=1,\ldots ,k$ and $h=1, 2, \ldots$ :

for the GARCH(p, q) model:

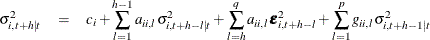
$\begin{eqnarray*} \sigma _{i,t+h|t}^2 & =& c_ i + \sum _{l=1}^{h-1} a_{ii,l} \sigma _{i,t+h-l|t}^2 + \sum _{l=h}^ q a_{ii,l} \bepsilon _{i,t+h-l}^2 + \sum _{l=1}^ p g_{ii,l} \sigma _{i,t+h-1|t}^2 \end{eqnarray*}$
for the EGARCH(p, q) model:

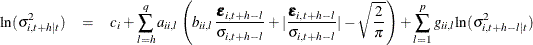
$\begin{eqnarray*} {\ln }(\sigma _{i,t+h|t}^2) & =& c_ i + \sum _{l=h}^{q} {a_{ii,l}\left(b_{ii,l}\frac{\bepsilon _{i,t+h-l}}{\sigma _{i,t+h-l}} + |\frac{\bepsilon _{i,t+h-l}}{\sigma _{i,t+h-l}}| - \sqrt {\frac{2}{\pi }}\right)} + \sum _{l=1}^{p}{g_{ii,l}{\ln }( \sigma _{i,t+h-l|t}^2)} \end{eqnarray*}$
for the QGARCH(p, q) model:

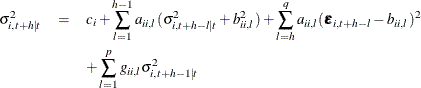
$\begin{eqnarray*} \sigma _{i,t+h|t}^2 & =& c_ i + \sum _{l=1}^{h-1}{a_{ii,l} (\sigma _{i,t+h-l|t}^2 + b_{ii,l}^2)} + \sum _{l=h}^{q}{a_{ii,l} (\bepsilon _{i,t+h-l} - b_{ii,l})^{2}} \\ & & + \sum _{l=1}^{p}{g_{ii,l} \sigma _{i,t+h-1|t}^2} \end{eqnarray*}$
for the TGARCH(p, q) model:

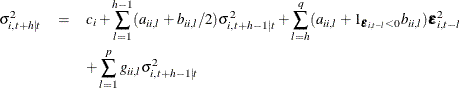
$\begin{eqnarray*} \sigma _{i,t+h|t}^2 & =& c_ i + \sum _{l=1}^{h-1} (a_{ii,l}+{b}_{ii,l}/2) \sigma _{i,t+h-1|t}^2 + \sum _{l=h}^ q (a_{ii,l}+1_{\bepsilon _{i,t-l}<0} {b}_{ii,l}) \bepsilon ^2_{i,t-l} \\ & & + \sum _{l=1}^ p {g_{ii,l} \sigma _{i,t+h-1|t}^2} \end{eqnarray*}$
for the PGARCH(p, q) model:

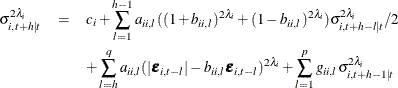
$\begin{eqnarray*} \sigma _{i,t+h|t}^{2\lambda _ i} & =& c_ i + \sum _{l=1}^{h-1}{ a_{ii,l} ( (1+b_{ii,l})^{2\lambda _ i} + (1-b_{ii,l})^{2\lambda _ i} ) \sigma _{i,t+h-l|t}^{2\lambda _ i}/2 } \\ & & + \sum _{l=h}^{q} { a_{ii,l} (|\bepsilon _{i,t-l}|-b_{ii,l}\bepsilon _{i,t-l})^{2\lambda _ i}} + \sum _{l=1}^ p { g_{ii,l} \sigma _{i,t+h-1|t}^{2\lambda _ i}} \end{eqnarray*}$

In the preceding equations, $\sigma _{i,s|t} = \sigma _{i,s}$ for $s \leq t$ . Then, the multistep forecast of conditional covariance matrix $H_{t+h|t}, h=1, 2, \ldots$ , is calculated by

$\begin{eqnarray*} H_{t+h|t} = D_{t+h|t} S D_{t+h|t} \end{eqnarray*}$

where $D_{t+h|t}$ is the diagonal matrix with element $\sigma _{i,t+h|t}, i=1, \ldots , k$ .

DCC Representation

Engle (2002) proposes a parsimonious parametric multivariate GARCH model that has time-varying conditional covariances and correlations.

The conditional covariance matrix $H_ t$ consists of

$\begin{eqnarray*} H_ t = D_ t \Gamma _ t D_ t \end{eqnarray*}$

where $D_ t$ is a $k \times k$ stochastic diagonal matrix with the element $\sigma _{i,t}$ and $\Gamma _ t$ is a $k \times k$ time-varying matrix with the typical element $\rho _{ij,t}$ .

The element of $H_ t$ is

$\begin{eqnarray*} h_{ij,t} & =& \rho _{ij,t}\sigma _{i,t}\sigma _{j,t} ~ ~ ~ ~ i,j=1,\ldots , k \end{eqnarray*}$

Note that $h_{ii,t}=\sigma _{i,t}^2, i=1,\ldots , k$ .

As in the CCC GARCH model, you can choose the type of GARCH model of interest by specifying the SUBFORM= option.

In the GARCH model,

$\begin{eqnarray*} \sigma _{i,t}^2 & =& c_ i + \sum _{l=1}^ q a_{ii,l} \bepsilon ^2_{i,t-l} + \sum _{l=1}^ p g_{ii,l} \sigma _{i,t-1}^2 ~ ~ ~ ~ i=1,\ldots , k \end{eqnarray*}$

In the EGARCH model, the conditional variance is an asymmetric function of lagged disturbances,

$\begin{eqnarray*} {\ln }( \sigma _{i,t}^2) & =& c_ i + \sum _{l=1}^{q} {a_{ii,l}\left(b_{ii,l}\frac{\bepsilon _{i,t-l}}{\sigma _{i,t-l}} +|\frac{\bepsilon _{i,t-l}}{\sigma _{i,t-l}}| -\sqrt {\frac{2}{\pi }}\right)} + \sum _{l=1}^{p}{g_{ii,l}{\ln }( \sigma _{i,t-l}^2)} ~ ~ ~ ~ i=1,\ldots , k\\ \end{eqnarray*}$

In the QGARCH model, the lagged errors’ centers are shifted from zero to some constant values,

$\begin{eqnarray*} \sigma _{i,t}^2 & =& c_ i + \sum _{l=1}^{q}{a_{ii,l} (\bepsilon _{i,t-l} - b_{ii,l})^{2}} + \sum _{l=1}^{p}{g_{ii,l} \sigma _{i,t-1}^2} ~ ~ ~ ~ i=1,\ldots , k\\ \end{eqnarray*}$

In the TGARCH model, each lagged squared error has an extra slope coefficient,

$\begin{eqnarray*} \sigma _{i,t}^2 & =& c_ i + \sum _{l=1}^ q (a_{ii,l}+1_{\bepsilon _{i,t-l}<0} {b}_{ii,l}) \bepsilon ^2_{i,t-l} + \sum _{l=1}^ p {g_{ii,l} \sigma _{i,t-1}^2} ~ ~ ~ ~ i=1,\ldots , k\\ \end{eqnarray*}$

where the indicator function $1_{{\bepsilon }_{i,t}<0}$ is one if ${\bepsilon }_{i,t}<0$ and zero otherwise.

The PGARCH model not only considers the asymmetric effect but also provides another way to model the long memory property in the volatility,

$\begin{eqnarray*} \sigma _{i,t}^{2\lambda _ i} = c_ i + \sum _{l=1}^{q}{ a_{ii,l} (|\bepsilon _{i,t-l}|-b_{ii,l}\bepsilon _{i,t-l})^{2\lambda _ i}} + \sum _{l=1}^ p {g_{ii,l} \sigma _{i,t-1}^{2\lambda _ i}} ~ ~ ~ ~ i=1,\ldots , k\\ \end{eqnarray*}$

where $\lambda _ i > 0$ and $|b_{ii,l}| \leq 1, l = 1, \ldots , q; i=1,\ldots , k$ .

The conditional correlation estimator $\rho _{ij,t}$ is

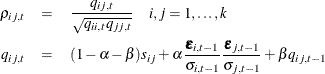
$\begin{eqnarray*} \rho _{ij,t} & =& \frac{q_{ij,t}}{\sqrt {q_{ii,t} q_{jj,t}}} ~ ~ ~ ~ i,j=1,\ldots , k\\ q_{ij,t} & =& (1-\alpha -\beta )s_{ij} + \alpha \frac{\bepsilon _{i,t-1}}{\sigma _{i,t-1}}\frac{\bepsilon _{j,t-1}}{\sigma _{j,t-1}} + \beta q_{ij,t-1} \end{eqnarray*}$

where $s_{ij}$ is the element of $S$ , the unconditional correlation matrix.

If you specify CORRCONSTANT=EXPECT, the element $s_{ij}$ of the unconditional correlation matrix $S$ is

$\begin{eqnarray*} s_{ij} = \frac{1}{T}\sum _{t=1}^{T}{\frac{\bepsilon _{i,t}}{\sigma _{i,t}}\frac{\bepsilon _{j,t}}{\sigma _{j,t}}} \end{eqnarray*}$

where $T$ is the sample size.

As shown in the CCC GARCH models, the following formulas are recursively implemented to obtain the multistep forecast of conditional error variance $\sigma _{i,t+h|t}^2, i=1,\ldots ,k$ and $h=1, 2, \ldots$ :

for the GARCH(p, q) model:

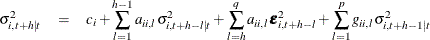
$\begin{eqnarray*} \sigma _{i,t+h|t}^2 & =& c_ i + \sum _{l=1}^{h-1} a_{ii,l} \sigma _{i,t+h-l|t}^2 + \sum _{l=h}^ q a_{ii,l} \bepsilon _{i,t+h-l}^2 + \sum _{l=1}^ p g_{ii,l} \sigma _{i,t+h-1|t}^2 \end{eqnarray*}$
for the EGARCH(p, q) model:

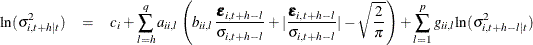
$\begin{eqnarray*} {\ln }(\sigma _{i,t+h|t}^2) & =& c_ i + \sum _{l=h}^{q} {a_{ii,l}\left(b_{ii,l}\frac{\bepsilon _{i,t+h-l}}{\sigma _{i,t+h-l}} + |\frac{\bepsilon _{i,t+h-l}}{\sigma _{i,t+h-l}}| - \sqrt {\frac{2}{\pi }}\right)} + \sum _{l=1}^{p}{g_{ii,l}{\ln }( \sigma _{i,t+h-l|t}^2)} \end{eqnarray*}$
for the QGARCH(p, q) model:

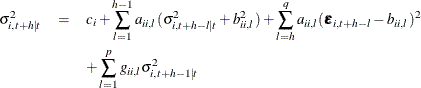
$\begin{eqnarray*} \sigma _{i,t+h|t}^2 & =& c_ i + \sum _{l=1}^{h-1}{a_{ii,l} (\sigma _{i,t+h-l|t}^2 + b_{ii,l}^2)} + \sum _{l=h}^{q}{a_{ii,l} (\bepsilon _{i,t+h-l} - b_{ii,l})^{2}} \\ & & + \sum _{l=1}^{p}{g_{ii,l} \sigma _{i,t+h-1|t}^2} \end{eqnarray*}$
for the TGARCH(p, q) model:

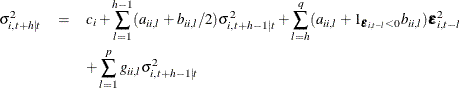
$\begin{eqnarray*} \sigma _{i,t+h|t}^2 & =& c_ i + \sum _{l=1}^{h-1} (a_{ii,l}+{b}_{ii,l}/2) \sigma _{i,t+h-1|t}^2 + \sum _{l=h}^ q (a_{ii,l}+1_{\bepsilon _{i,t-l}<0} {b}_{ii,l}) \bepsilon ^2_{i,t-l} \\ & & + \sum _{l=1}^ p {g_{ii,l} \sigma _{i,t+h-1|t}^2} \end{eqnarray*}$
for the PGARCH(p, q) model:

$\begin{eqnarray*} \sigma _{i,t+h|t}^{2\lambda _ i} & =& c_ i + \sum _{l=1}^{h-1}{ a_{ii,l} ( (1+b_{ii,l})^{2\lambda _ i} + (1-b_{ii,l})^{2\lambda _ i} ) \sigma _{i,t+h-l|t}^{2\lambda _ i}/2 } \\ & & + \sum _{l=h}^{q} { a_{ii,l} (|\bepsilon _{i,t-l}|-b_{ii,l}\bepsilon _{i,t-l})^{2\lambda _ i}} + \sum _{l=1}^ p { g_{ii,l} \sigma _{i,t+h-1|t}^{2\lambda _ i}} \end{eqnarray*}$

In the preceding equations, $\sigma _{i,s|t} = \sigma _{i,s}$ for $s \leq t$ . Then, the multistep forecast of conditional covariance matrix $H_{t+h|t}, h=1, 2, \ldots$ , is calculated by

$\begin{eqnarray*} H_{t+h|t} = D_{t+h|t} \Gamma _{t+h|t} D_{t+h|t} \end{eqnarray*}$

where $D_{t+h|t}$ is the diagonal matrix with element $\sigma _{i,t+h|t}, i=1, \ldots , k$ , and $\Gamma _{t+h|t}$ is the matrix with element $\rho _{ij,t+h|t},i,j=1,\ldots , k$ ,

$\begin{eqnarray*} \rho _{ij,t+h|t} & =& \frac{q_{ij,t+h|t}}{\sqrt {q_{ii,t+h|t} q_{jj,t+h|t}}} \\ q_{ij,t+h|t} & =& \begin{cases} (1-\alpha -\beta )s_{ij} + \alpha \frac{\bepsilon _{i,t}}{\sigma _{i,t}}\frac{\bepsilon _{j,t}}{\sigma _{j,t}} + \beta q_{ij,t} & ~ ~ ~ ~ h=1\\ (1-\alpha -\beta )s_{ij} + \alpha q_{ij,t+h-1|t} + \beta q_{ij,t+h-1|t} & ~ ~ ~ ~ h>1\\ \end{cases}\end{eqnarray*}$

Estimation of GARCH Model

The log-likelihood function of the multivariate GARCH model is written without a constant term as

$\begin{eqnarray*} \ell = - \frac{1}{2}\sum _{t=1}^{T} [ \log |H_ t| + \bepsilon _{t}’H_ t^{-1}\bepsilon _{t} ] \end{eqnarray*}$

The log-likelihood function is maximized by an iterative numerical method such as quasi-Newton optimization. The starting values for the regression parameters are obtained from the least squares estimates. The covariance of $\bepsilon _{t}$ is used as the starting values for the GARCH constant parameters, and the starting value for the other GARCH parameters is either $10^{-6}$ or $10^{-3}$ , depending on the GARCH model’s representation.

Prediction of Endogenous (Dependent) Variables

In multivariate GARCH models, the optimal (minimum MSE) l-step-ahead forecast of endogenous variables $\mb{y}_{t+l|t}$ uses the same formula as shown in the section Forecasting. However, the exogenous (independent) variables, if present, are always assumed to be nonstochastic (deterministic); that is, to predict the endogenous variables, you must specify the future values of the exogenous variables. The prediction error of the optimal l-step-ahead forecast is $\mb{e} _{t+l|t} = \mb{y} _{t+l}-\mb{y} _{t+l|t} = \sum _{j=0}^{l-1}\Psi _{j}\bepsilon _{t+l-j}$ , with zero mean and covariance matrix,

$\Sigma _{t}(l) = \mr{Cov} (\mb{e} _{t+l|t} ) = \sum _{j=0}^{l-1}\Psi _{j} H_{t+l-j|t} \Psi _{j}’$

where $H_{t+h|t}, h=1, \ldots , l,$ is the h-step-ahead forecast of the conditional covariance matrix. As emphasized by the subscript t, $\Sigma _{t}(l)$ is time-dependent. In the OUT= data set, the forecast standard errors and prediction intervals are constructed according to $\Sigma _{t}(l)$ . If you specify the COVPE option, the prediction error covariances that are output in the CovPredictError and CovPredictErrorbyVar ODS tables are based on the time-independent formula

$\Sigma (l) = \sum _{j=0}^{l-1}\Psi _{j}\Sigma \Psi _{j}’$

where $\Sigma$ is the unconditional covariance matrix of innovations. The decomposition of the prediction error covariances is also based on $\Sigma (l)$ .

Covariance Stationarity

Define the multivariate GARCH process as

$\mb{h} _ t = \sum _{i=1}^\infty G(B)^{i-1}[\mb{c} +A(B)\bm {\eta }_ t]$

where $\mb{h} _ t = \mbox{vec}(H_{t})$ , $\mb{c} = \mbox{vec}(C_0)$ , and $\bm {\eta }_ t = \mbox{vec}(\bepsilon _{t}\bepsilon _{t}’)$ . This representation is equivalent to a GARCH( $p,q$ ) model by the following algebra:

$\begin{eqnarray*} \mb{h}_ t & =& \mb{c} + A(B)\bm {\eta }_ t + \sum _{i=2}^\infty G(B)^{i-1}[\mb{c} +A(B)\bm {\eta }_ t] \\ & =& \mb{c} + A(B)\bm {\eta }_ t + G(B)\sum _{i=1}^\infty G(B)^{i-1}[tmb{c} +A(B)\bm {\eta }_ t] \\ & =& \mb{c} + A(B)\bm {\eta }_ t + G(B) \mb{h}_ t \end{eqnarray*}$

Defining $A(B)= \sum _{i=1}^ q (A_ i \otimes A_ i)’B^ i$ and $G(B)= \sum _{i=1}^ p (G_ i \otimes G_ i)’B^ i$ gives a BEKK representation.

The necessary and sufficient conditions for covariance stationarity of the multivariate GARCH process are that all the eigenvalues of $A(1)+G(1)$ are less than 1 in modulus.

An Example of a VAR(1)–ARCH(1) Model

The following DATA step simulates a bivariate vector time series to provide test data for the multivariate GARCH model:

data garch;
   retain seed 16587;
   esq1 = 0; esq2 = 0;
   ly1 = 0;  ly2 = 0;
   do i = 1 to 1000;
      ht = 6.25 + 0.5*esq1;
      call rannor(seed,ehat);
      e1 = sqrt(ht)*ehat;
      ht = 1.25 + 0.7*esq2;
      call rannor(seed,ehat);
      e2 = sqrt(ht)*ehat;
      y1 = 2 + 1.2*ly1 - 0.5*ly2 + e1;
      y2 = 4 + 0.6*ly1 + 0.3*ly2 + e2;
      if i>500 then output;
      esq1 = e1*e1; esq2 = e2*e2;
      ly1 = y1;  ly2 = y2;
   end;
   keep y1 y2;
run;

The following statements fit a VAR(1)–ARCH(1) model to the data. For a VAR-ARCH model, you specify the order of the autoregressive model with the P=1 option in the MODEL statement and the Q=1 option in the GARCH statement. In order to produce the initial and final values of parameters, the TECH=QN option is specified in the NLOPTIONS statement.

proc varmax data=garch;
   model y1 y2 / p=1
         print=(roots estimates diagnose);
   garch q=1;
   nloptions tech=qn;
run;

Figure 35.61 through Figure 35.65 show the details of this example. Figure 35.61 shows the initial values of parameters.

Figure 35.61: Start Parameter Estimates for the VAR(1)–ARCH(1) Model

The VARMAX Procedure

Optimization Start
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function
1	CONST1	2.249575	0.000082533
2	CONST2	3.902673	0.000401
3	AR1_1_1	1.231775	0.000105
4	AR1_2_1	0.576890	-0.004811
5	AR1_1_2	-0.528405	0.000617
6	AR1_2_2	0.343714	0.001811
7	GCHC1_1	9.929763	0.151293
8	GCHC1_2	0.193163	-0.014305
9	GCHC2_2	4.063245	0.370333
10	ACH1_1_1	0.001000	-0.667182
11	ACH1_2_1	0	-0.068905
12	ACH1_1_2	0	-0.734486
13	ACH1_2_2	0.001000	-3.127035

Figure 35.62 shows the final parameter estimates.

Figure 35.62: Results of Parameter Estimates for the VAR(1)–ARCH(1) Model

The VARMAX Procedure

Optimization Results
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function
1	CONST1	2.156865	0.000246
2	CONST2	4.048879	0.000105
3	AR1_1_1	1.224620	-0.001957
4	AR1_2_1	0.609651	0.000173
5	AR1_1_2	-0.534248	-0.000468
6	AR1_2_2	0.302599	-0.000375
7	GCHC1_1	8.238625	-0.000056090
8	GCHC1_2	-0.231183	-0.000021724
9	GCHC2_2	1.565459	0.000110
10	ACH1_1_1	0.374255	-0.000419
11	ACH1_2_1	0.035883	-0.000606
12	ACH1_1_2	0.057461	0.001636
13	ACH1_2_2	0.717897	-0.000149

Figure 35.63 shows the conditional variance by using the BEKK representation of the ARCH(1) model. The ARCH parameters are estimated as follows by the vectorized parameter matrices:

$\begin{eqnarray*} \bepsilon _ t|\mathcal{F}(t-1) & \sim & N(0,H_ t) \\ H_ t & = & \left[ \begin{matrix} 8.23863 & -0.23118 \\ -0.23118 & 1.56546 \\ \end{matrix} \right] \\ & + & \left[ \begin{matrix} 0.37426 & 0.05746 \\ 0.03588 & 0.71790 \\ \end{matrix} \right]’ \bepsilon _{t-1}\bepsilon _{t-1}’ \left[ \begin{matrix} 0.37426 & 0.05746 \\ 0.03588 & 0.71790 \\ \end{matrix} \right] \end{eqnarray*}$

Figure 35.63: ARCH(1) Parameter Estimates for the VAR(1)–ARCH(1) Model

The VARMAX Procedure

Type of Model	VAR(1)-ARCH(1)
Estimation Method	Maximum Likelihood Estimation
Representation Type	BEKK

GARCH Model Parameter Estimates
Parameter	Estimate	Standard Error	t Value	Pr > \|t\|
GCHC1_1	8.23863	0.72663	11.34	0.0001
GCHC1_2	-0.23118	0.21434	-1.08	0.2813
GCHC2_2	1.56546	0.19407	8.07	0.0001
ACH1_1_1	0.37426	0.07502	4.99	0.0001
ACH1_2_1	0.03588	0.06974	0.51	0.6071
ACH1_1_2	0.05746	0.02597	2.21	0.0274
ACH1_2_2	0.71790	0.06895	10.41	0.0001

Figure 35.64 shows the AR parameter estimates and their significance.

The fitted VAR(1) model with the previous conditional covariance ARCH model is written as follows:

$\mb{y} _ t = \left[ \begin{matrix} 2.15687 \\ 4.04888 \\ \end{matrix} \right] + \left[ \begin{matrix} 1.22462 & -0.53425 \\ 0.60965 & 0.30260 \\ \end{matrix} \right] \mb{y} _{t-1} + \bepsilon _ t$

Figure 35.64: VAR(1) Parameter Estimates for the VAR(1)–ARCH(1) Model

Model Parameter Estimates
Equation	Parameter	Estimate	Standard Error	t Value	Pr > \|t\|	Variable
y1	CONST1	2.15687	0.21717	9.93	0.0001	1
	AR1_1_1	1.22462	0.02542	48.17	0.0001	y1(t-1)
	AR1_1_2	-0.53425	0.02807	-19.03	0.0001	y2(t-1)
y2	CONST2	4.04888	0.10663	37.97	0.0001	1
	AR1_2_1	0.60965	0.01216	50.13	0.0001	y1(t-1)
	AR1_2_2	0.30260	0.01491	20.30	0.0001	y2(t-1)

Figure 35.65 shows the roots of the AR and ARCH characteristic polynomials. The eigenvalues have a modulus less than one.

Figure 35.65: Roots for the VAR(1)–ARCH(1) Model

Roots of AR Characteristic Polynomial
Index	Real	Imaginary	Modulus	Radian	Degree
1	0.76361	0.33641	0.8344	0.4150	23.7762
2	0.76361	-0.33641	0.8344	-0.4150	-23.7762

Roots of GARCH Characteristic Polynomial
Index	Real	Imaginary	Modulus	Radian	Degree
1	0.52388	0.00000	0.5239	0.0000	0.0000
2	0.26661	0.00000	0.2666	0.0000	0.0000
3	0.26661	0.00000	0.2666	0.0000	0.0000
4	0.13569	0.00000	0.1357	0.0000	0.0000