The VARMAX Procedure

VAR and VARX Modeling

Subsections:

The pth-order VAR process is written as

\begin{eqnarray*} \mb{y} _{t} -\bmu = \sum _{i=1}^{p}\Phi _ i(\mb{y} _{t-i}-\bmu ) + \bepsilon _ t ~ ~ \mr{or} ~ ~ \Phi (B)( \mb{y} _{t} - \bmu ) = \bepsilon _ t \end{eqnarray*}

with $\Phi (B) = I_ k - \sum _{i=1}^{p} \Phi _ i B^ i$.

Equivalently, it can be written as

\begin{eqnarray*} \mb{y} _{t} = \bdelta + \sum _{i=1}^{p}\Phi _ i\mb{y} _{t-i} + \bepsilon _ t ~ ~ \mr{or} ~ ~ \Phi (B) \mb{y} _{t} = \bdelta + \bepsilon _ t \end{eqnarray*}

with $\bdelta = (I_ k-\sum _{i=1}^{p}\Phi _ i)\bmu $.

Stationarity

For stationarity, the VAR process must be expressible in the convergent causal infinite MA form as

\begin{eqnarray*} \mb{y} _{t} = \bmu + \sum _{j=0}^{\infty }\Psi _ j\bepsilon _{t-j} \end{eqnarray*}

where $\Psi (B) = \Phi (B)^{-1} = \sum _{j=0}^{\infty }\Psi _ jB^ j$ with $\sum _{j=0}^{\infty }||\Psi _ j|| <\infty $, where $||A||$ denotes a norm for the matrix $A$ such as $||A||^2 = \mr{tr} \{ A’A\} $. The matrix $\Psi _ j$ can be recursively obtained from the relation $\Phi (B)\Psi (B)=I$; it is

\begin{eqnarray*} \Psi _ j = \Phi _1 \Psi _{j-1}+\Phi _2 \Psi _{j-2}+\cdots +\Phi _ p \Psi _{j-p} \end{eqnarray*}

where $\Psi _0 = I_ k$ and $\Psi _ j = 0$ for $j < 0$.

The stationarity condition is satisfied if all roots of $|\Phi (z)|= 0$ are outside of the unit circle. The stationarity condition is equivalent to the condition in the corresponding VAR(1) representation, $\mb{Y} _ t = \Phi \mb{Y} _{t-1} + \bm {\varepsilon }_ t $, that all eigenvalues of the $kp \times kp$ companion matrix $\Phi $ be less than one in absolute value, where $\mb{Y} _ t = (\mb{y} _ t’,\ldots ,\mb{y} _{t-p+1}’)’$, $\bm {\varepsilon }_ t = ( \bepsilon _ t’,0’, \ldots , 0’)’$, and

\begin{eqnarray*} \Phi = \left[ \begin{matrix} \Phi _1 & \Phi _2 & \cdots & \Phi _{p-1} & \Phi _{p} \\ I_ k & 0 & \cdots & 0 & 0 \\ 0 & I_ k & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & I_ k & 0 \\ \end{matrix} \right] \end{eqnarray*}

If the stationarity condition is not satisfied, a nonstationary model (a differenced model or an error correction model) might be more appropriate.

The following statements estimate a VAR(1) model and use the ROOTS option to compute the characteristic polynomial roots: 

proc varmax data=simul1;
   model y1 y2 / p=1 noint print=(roots);
run;

Figure 35.44 shows the output associated with the ROOTS option, which indicates that the series is stationary since the modulus of the eigenvalue is less than one.

Figure 35.44: Stationarity (ROOTS Option)

The VARMAX Procedure

Roots of AR Characteristic Polynomial
Index Real Imaginary Modulus Radian Degree
1 0.77238 0.35899 0.8517 0.4351 24.9284
2 0.77238 -0.35899 0.8517 -0.4351 -24.9284 




               

               


            

            

               

                  

                     

                        

Parameter Estimation
                        

                     

                  

               

               
 Consider the stationary VAR(p) model 
               

               

                  
\begin{eqnarray*}  \mb{y} _{t} = \bdelta + \sum _{i=1}^{p}\Phi _ i\mb{y} _{t-i} + \bepsilon _ t \end{eqnarray*}

               

               
 where $\mb{y} _{-p+1}, \ldots , \mb{y} _{0}$ are assumed to be available (for convenience of notation). This can be represented by the general form of the multivariate
                  linear model, 
               

               

                  
\begin{eqnarray*}  Y = XB + E \; \; \mbox{or}\; \; \mb{y} = (X \otimes I_ k)\bbeta + \mb{e} \end{eqnarray*}

               

               
 where 

               

                  
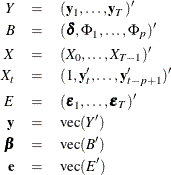
\begin{eqnarray*}  Y &  = &  (\mb{y} _{1},\ldots ,\mb{y} _ T)’ \\ B &  = &  (\bdelta , \Phi _1,\ldots ,\Phi _ p)’ \\ X &  = &  (X_{0},\ldots ,X_{T-1})’ \\ X_ t &  = &  (1, \mb{y} ’_{t},\ldots ,\mb{y} ’_{t-p+1})’ \\ E &  = &  (\bepsilon _{1},\ldots ,\bepsilon _ T)’ \\ \mb{y} &  = &  \mbox{vec}(Y’) \\ \bbeta &  = &  \mbox{vec}(B’) \\ \mb{e} &  = &  \mbox{vec}(E’) \end{eqnarray*}

               

               
 with vec denoting the column stacking operator. 
               

               
The conditional least squares estimator of $\bbeta $ is 
               

               

                  
\[  \hat{ \bbeta } = ( (X’X)^{-1}X’\otimes I_ k)\mb{y}  \]

               

               
 and the estimate of $\Sigma $ is 
               

               

                  
\[  \hat\Sigma = (T-(kp+1))^{-1}\sum _{t=1}^ T \hat{\bepsilon _ t} \hat{\bepsilon _ t}’  \]

               

               
 where $ \hat{\bepsilon _ t}$ is the residual vectors. Consistency and asymptotic normality of the LS estimator are that 
               

               

                  
\[  \sqrt {T}(\hat{\bbeta } -\bbeta )\stackrel{d}{\rightarrow } N(0, \Gamma _ p^{-1} \otimes \Sigma )  \]

               

               
 where $X’X/T$ converges in probability to $\Gamma _ p$ and $\stackrel{d}{\rightarrow }$ denotes convergence in distribution. 
               

               
The (conditional) maximum likelihood estimator in the VAR(p) model is equal to the (conditional) least squares estimator on the assumption of normality of the error vectors. 
               

               

            

            

               

                  

                     

                        

Asymptotic Distributions of Impulse Response Functions
                        

                     

                  

               

               
 As before, vec denotes the column stacking operator and vech is the corresponding operator that stacks the elements on and below the diagonal. For any $k\times k$ matrix $A$, the commutation matrix $K_ k$ is defined as $K_ k \mr{vec} (A) = \mr{vec} (A’)$; the duplication matrix $D_ k$ is defined as $D_ k \mr{vech} (A) = \mr{vec} (A)$; the elimination matrix $L_ k$ is defined as $L_ k \mr{vec} (A) = \mr{vech} (A)$. 
               

               
The asymptotic distribution of the impulse response function (Lütkepohl, 1993) is 
               

               

                  
\[  \sqrt {T} \mr{vec} (\hat\Psi _ j - \Psi _ j ) \stackrel{d}{\rightarrow } N(0, G_ j\Sigma _{\bbeta } G_ j’) ~ ~ j=1,2,\ldots  \]

               

               
 where $\Sigma _{\bbeta } = \Gamma _ p^{-1} \otimes \Sigma $ and 
               

               

                  
\[  G_ j= \frac{\partial \mr{vec} (\Psi _ j)}{\partial {\bbeta }'} = \sum _{i=0}^{j-1} \mb{J} ({\bPhi }’)^{j-1-i}\otimes \Psi _ i  \]

               

               
 where $\mb{J} = [ I_ k, 0,\ldots , 0 ]$ is a $k\times kp$ matrix and ${\bPhi }$ is a $kp\times kp$ companion matrix. 
               

               
The asymptotic distribution of the accumulated impulse response function is 

               

                  
\[  \sqrt {T} \mr{vec} (\hat\Psi ^{a}_ l - \Psi ^{a}_ l ) \stackrel{d}{\rightarrow } N(0, F_ l\Sigma _{\bbeta } F_ l’) ~ ~ l=1,2,\ldots  \]

               

               
 where $F_ l=\sum _{j=1}^ l G_ j$. 
               

               
The asymptotic distribution of the orthogonalized impulse response function is 

               

                  
\[  \sqrt {T} \mr{vec} (\hat\Psi ^{o}_ j - \Psi ^{o}_ j ) \stackrel{d}{\rightarrow } N(0, C_ j\Sigma _{\bbeta } C_ j’ +\bar{C_ j}\Sigma _{\bsigma } \bar{C_ j'}) ~ ~ j=0,1,2,\ldots  \]

               

               
 where $C_0=0$, $C_ j=(\Psi ^{o'}_0\otimes I_ k )G_ j$, $\bar{C_ j} =(I_ k \otimes \Psi _ j)H$, 
               

               

                  
\[  H=\frac{\partial \mr{vec} (\Psi ^{o}_0)}{\partial {\bsigma }'} =L’_ k\{ L_ k(I_{k^2}+K_ k)(\Psi ^{o}_0 \otimes I_ k)L’_ k\} ^{-1}  \]

               

               
 and $\Sigma _{\bsigma }= 2D_ k^{+}(\Sigma \otimes \Sigma )D_ k^{+'}$ with $D_ k^{+} = (D’_ k D_ k)^{-1}D’_ k$ and $\bsigma =\mr{vech(\Sigma ) }$. 
               

               

            

            

               

                  

                     

                        

Granger Causality Test
                        

                     

                  

               

               
 Let $\mb{y} _ t$ be arranged and partitioned in subgroups $\mb{y} _{1t}$ and $\mb{y} _{2t}$ with dimensions $k_1$ and $k_2$, respectively ($k=k_1+k_2$); that is, $\mb{y} _ t = (\mb{y} _{1t}’,\mb{y} _{2t}’)’$ with the corresponding white noise process $\bepsilon _ t = (\bepsilon _{1t}’,\bepsilon _{2t}’)’$. Consider the VAR(p) model with partitioned coefficients $\Phi _{ij}(B)$ for $i,j=1,2$ as follows: 
               

               

                  
\begin{eqnarray*}  \left[\begin{matrix}  \Phi _{11}(B)   &  \Phi _{12}(B)   \\ \Phi _{21}(B)   &  \Phi _{22}(B)   \\ \end{matrix}\right] \left[\begin{matrix}  \mb{y} _{1t}   \\ \mb{y} _{2t}   \\ \end{matrix}\right] = \left[\begin{matrix}  \bdelta _{1}   \\ \bdelta _{2}   \\ \end{matrix}\right] + \left[\begin{matrix}  \bepsilon _{1t}   \\ \bepsilon _{2t}   \\ \end{matrix}\right] \end{eqnarray*}

               

               
 The variables $\mb{y} _{1t}$ are said to cause $\mb{y} _{2t}$, but $\mb{y} _{2t}$ do not cause $\mb{y} _{1t}$ if $\Phi _{12}(B)=0$. The implication of this model structure is that future values of the process $\mb{y} _{1t}$ are influenced only by its own past and not by the past of $\mb{y} _{2t}$, where future values of $\mb{y} _{2t}$ are influenced by the past of both $\mb{y} _{1t}$ and $\mb{y} _{2t}$. If the future $\mb{y} _{1t}$ are not influenced by the past values of $\mb{y} _{2t}$, then it can be better to model $\mb{y} _{1t}$ separately from $\mb{y} _{2t}$. 
               

               
Consider testing $H_0\colon C\bbeta = c$, where C is a $s \times (k^2p+k)$ matrix of rank s and c is an s-dimensional vector where $s=k_1k_2p$. Assuming that 
               

               

                  
\[  \sqrt {T}(\hat{\bbeta } -\bbeta )\stackrel{d}{\rightarrow } N(0, \Gamma _ p^{-1} \otimes \Sigma )  \]

               

               
 you get the Wald statistic 

               

                  
\[  T(C \hat{\bbeta } -c)’ [C({\hat\Gamma _ p}^{-1} \otimes {\hat\Sigma })C’]^{-1} (C \hat{\bbeta } -c) \stackrel{d}{\rightarrow } \chi ^2(s)  \]

               

               
 For the Granger causality test, the matrix C consists of zeros or ones and c is the zero vector. See Lütkepohl (1993) for more details of the Granger causality test. 
               

               

            

            

               

                  

                     

                        

VARX Modeling
                        

                     

                  

               

               
 The vector autoregressive model with exogenous variables is called the VARX(p,s) model. The form of the VARX(p,s) model can be written as 
               

               

                  
\begin{eqnarray*}  \mb{y} _ t = \bdelta + \sum _{i=1}^{p} \Phi _ i\mb{y} _{t-i} + \sum _{i=0}^{s}\Theta ^*_ i\mb{x} _{t-i} + \bepsilon _ t \end{eqnarray*}

               

               
 The parameter estimates can be obtained by representing the general form of the multivariate linear model, 

               

                  
\begin{eqnarray*}  Y = XB + E \; \; \mbox{or}\; \; \mb{y} = (X \otimes I_ k)\bbeta + \mb{e} \end{eqnarray*}

               

               
 where 

               

                  
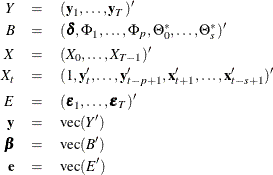
\begin{eqnarray*}  Y &  = &  (\mb{y} _{1},\ldots ,\mb{y} _ T)’ \\ B &  = &  (\bdelta , \Phi _1,\ldots ,\Phi _ p, \Theta ^*_0,\ldots ,\Theta ^*_ s)’ \\ X &  = &  (X_{0},\ldots ,X_{T-1})’ \\ X_ t &  = &  (1, \mb{y} ’_{t},\ldots ,\mb{y} ’_{t-p+1}, \mb{x} ’_{t+1},\ldots ,\mb{x} ’_{t-s+1})’ \\ E &  = &  (\bepsilon _{1},\ldots ,\bepsilon _ T)’ \\ \mb{y} &  = &  \mbox{vec}(Y’) \\ \bbeta &  = &  \mbox{vec}(B’) \\ \mb{e} &  = &  \mbox{vec}(E’) \end{eqnarray*}

               

               
 The conditional least squares estimator of $\beta $ can be obtained by using the same method in a VAR(p) modeling. If the multivariate linear model has different independent variables that correspond to dependent variables, the
                  SUR (seemingly unrelated regression) method is used to improve the regression estimates. 
               

               
The following example fits the ordinary regression model: 


   proc varmax data=one;
      model y1-y3 = x1-x5;
   run;



 This is equivalent to the REG procedure in the SAS/STAT software: 


   proc reg data=one;
      model y1 = x1-x5;
      model y2 = x1-x5;
      model y3 = x1-x5;
   run;



The following example fits the second-order lagged regression model: 


   proc varmax data=two;
      model y1 y2 = x / xlag=2;
   run;



This is equivalent to the REG procedure in the SAS/STAT software: 


   data three;
      set two;
      xlag1 = lag1(x);
      xlag2 = lag2(x);
   run;

   proc reg data=three;
      model y1 = x xlag1 xlag2;
      model y2 = x xlag1 xlag2;
   run;



The following example fits the ordinary regression model with different regressors: 


   proc varmax data=one;
      model y1 = x1-x3, y2 = x2 x3;
   run;



This is equivalent to the following SYSLIN procedure statements: 


   proc syslin data=one vardef=df sur;
      endogenous y1 y2;
      model y1 = x1-x3;
      model y2 = x2 x3;
   run;



From the output in Figure 35.20 in the section Getting Started: VARMAX Procedure, you can see that the parameters, XL0_1_2, XL0_2_1, XL0_3_1, and XL0_3_2 associated with the exogenous variables, are not
                  significant. The following example fits the VARX(1,0) model with different regressors: 
               


proc varmax data=grunfeld;
   model y1 = x1, y2 = x2, y3 / p=1 print=(estimates);
run;



  

               


Figure 35.45: Parameter Estimates for the VARX(1, 0) Model

                  

                     

                        
                        

                           
                           
                           
The VARMAX Procedure

                           
                           

                           
                           

                              
                              

                                 
                                 












XLag
                                          
                                       



Lag
                                          
                                          Variable
                                          
                                          x1
                                          
                                          x2
                                          
                                       





0
                                          
                                          y1
                                          
                                          1.83231
                                          
                                          _
                                          
                                       



 
                                          
                                          y2
                                          
                                          _
                                          
                                          2.42110
                                          
                                       



 
                                          
                                          y3
                                          
                                          _
                                          
                                          _
                                          
                                       






                              
                           

                           



                        
                        
                     





               

               


               
As you can see in Figure 35.45, the symbol ‘_’ in the elements of matrix corresponds to endogenous variables that do not take the denoted exogenous variables.