-
ACCEPTTOL=n
-
specifies a tolerance for acceptance probabilities. By default, ACCEPTTOL=0.075.
-
AUTOCORLAG=n
ACLAG=n
-
specifies the maximum number of autocorrelation lags used in computing the effective sample size; see the section Effective Sample Size in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details. The value is used in the calculation of the Monte Carlo standard error; see the section Standard Error of the Mean Estimate in Chapter 7: Introduction to Bayesian Analysis Procedures. By default, AUTOCORLAG=MIN(500, MCsample/4), where MCsample is the Markov chain sample size kept after thinning—that is,
MCsample ![$ = \left[ \frac{\mbox{NMC}}{\mbox{NTHIN}} \right] $](images/statug_mcmc0046.png) . If AUTOCORLAG= is set too low, you might observe significant lags, and the effective sample size cannot be calculated accurately.
A WARNING message appears, and you can either increase AUTOCORLAG= or NMC=
, accordingly.
. If AUTOCORLAG= is set too low, you might observe significant lags, and the effective sample size cannot be calculated accurately.
A WARNING message appears, and you can either increase AUTOCORLAG= or NMC=
, accordingly.
-
DISCRETE=keyword
-
specifies the proposal distribution used in sampling discrete parameters. The default is DISCRETE=BINNING.
The keyword values are as follows:
-
BINNING
-
uses continuous proposal distributions for all discrete parameter blocks. The proposed sample is then discretized (binned)
before further calculations. This sampling method approximates the correlation structure among the discrete parameters in
the block and could improve mixing in some cases.
-
GEO
-
uses independent symmetric geometric proposal distributions for all discrete parameter blocks. This proposal does not take
parameter correlations into account. However, it can work better than the BINNING option in cases where the range of the parameters
is relatively small and a normal approximation can perform poorly.
-
DIAGNOSTICS=NONE | (keyword-list)
DIAG=NONE | (keyword-list)
-
specifies options for MCMC convergence diagnostics. By default, PROC MCMC computes the Geweke test, sample autocorrelations,
effective sample sizes, and Monte Carlo errors. The Raftery-Lewis and Heidelberger-Welch tests are also available. See the
section Assessing Markov Chain Convergence in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details on convergence diagnostics. You can request all of the diagnostic tests by specifying DIAGNOSTICS=ALL. You
can suppress all the tests by specifying DIAGNOSTICS=NONE.
You can use postprocessing autocall macros to calculate convergence diagnostics of the posterior samples after PROC MCMC has
exited. See the section Autocall Macros for Postprocessing.
The following options are available.
-
ALL
-
computes all diagnostic tests and statistics. You can combine the option ALL with any other specific tests to modify test
options. For example DIAGNOSTICS=(ALL AUTOCORR(LAGS=(1 5 35))) computes all tests with default settings and autocorrelations
at lags 1, 5, and 35.
-
AUTOCORR <(autocorr-options)>
-
computes default autocorrelations at lags 1, 5, 10, and 50 for each variable. You can choose other lags by using the following
autocorr-options:
-
LAGS | AC=numeric-list
-
specifies autocorrelation lags. The numeric-list must take positive integer values.
-
ESS
-
computes the effective sample sizes (Kass et al. (1998)) of the posterior samples of each parameter. It also computes the correlation time and the efficiency of the chain for each
parameter. Small values of ESS might indicate a lack of convergence. See the section Effective Sample Size in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details.
-
GEWEKE <(Geweke-options)>
-
computes the Geweke spectral density diagnostics; this is a two-sample t-test between the first 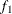 portion and the last
portion and the last 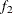 portion of the chain. See the section Geweke Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details. The default is FRAC1=0.1 and FRAC2=0.5, but you can choose other fractions by using the following Geweke-options:
portion of the chain. See the section Geweke Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details. The default is FRAC1=0.1 and FRAC2=0.5, but you can choose other fractions by using the following Geweke-options:
-
FRAC1 | F1=value
-
specifies the beginning FRAC1 proportion of the Markov chain. By default, FRAC1=0.1.
-
FRAC2 | F2=value
-
specifies the end FRAC2 proportion of the Markov chain. By default, FRAC2=0.5.
-
HEIDELBERGER | HEIDEL <(Heidel-options)>
-
computes the Heidelberger and Welch diagnostic (which consists of a stationarity test and a halfwidth test) for each variable.
The stationary diagnostic test tests the null hypothesis that the posterior samples are generated from a stationary process.
If the stationarity test is passed, a halfwidth test is then carried out. See the section Heidelberger and Welch Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details.
These diagnostics are not performed by default. You can specify the DIAGNOSTICS=HEIDELBERGER option to request these diagnostics,
and you can also specify suboptions, such as DIAGNOSTICS=HEIDELBERGER(EPS=0.05), as follows:
-
MCSE
MCERROR
-
computes the Monte Carlo standard error for the posterior samples of each parameter.
-
NONE
-
suppresses all of the diagnostic tests and statistics. This is not recommended.
-
RAFTERY | RL <(Raftery-options)>
-
computes the Raftery and Lewis diagnostics, which evaluate the accuracy of the estimated quantile (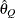 for a given Q
for a given Q 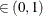 ) of a chain.
) of a chain. 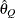 can achieve any degree of accuracy when the chain is allowed to run for a long time. The algorithm stops when the estimated
probability
can achieve any degree of accuracy when the chain is allowed to run for a long time. The algorithm stops when the estimated
probability 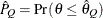 reaches within
reaches within 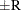 of the value Q with probability S; that is,
of the value Q with probability S; that is, 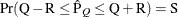 . See the section Raftery and Lewis Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details. The Raftery-options enable you to specify Q, R, S, and a precision level
. See the section Raftery and Lewis Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details. The Raftery-options enable you to specify Q, R, S, and a precision level  for a stationary test.
for a stationary test.
These diagnostics are not performed by default. You can specify the DIAGNOSTICS=RAFERTY option to request these diagnostics,
and you can also specify suboptions, such as DIAGNOSTICS=RAFERTY(QUANTILE=0.05), as follows:
-
QUANTILE | Q=value
-
specifies the order (a value between 0 and 1) of the quantile of interest. By default, QUANTILE=0.025.
-
ACCURACY | R=value
-
specifies a small positive number as the margin of error for measuring the accuracy of estimation of the quantile. By default,
ACCURACY=0.005.
-
PROB | S=value
-
specifies the probability of attaining the accuracy of the estimation of the quantile. By default, PROB=0.95.
-
EPS=value
-
specifies the tolerance level (a small positive number) for the stationary test. By default, EPS=0.001.
-
DIC
-
computes the Deviance Information Criterion (DIC). DIC is calculated using the posterior mean estimates of the parameters.
See the section Deviance Information Criterion (DIC) in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details.
-
DATA=SAS-data-set
-
specifies the input data set. Observations in this data set are used to compute the log-likelihood function that you specify
with PROC MCMC statements.
-
INF=value
-
specifies the numerical definition of infinity in PROC MCMC. The default is INF=1E15. For example, PROC MCMC considers 1E16
to be outside of the support of the normal distribution and assigns a missing value to the log density evaluation. You can
select a larger value with the INF= option. The minimum value allowed is 1E10.
-
INIT=(keyword-list)
-
specifies options for generating the initial values for the parameters. These options apply only to prior distributions that
are recognized by PROC MCMC. See the section Standard Distributions for a list of these distributions. If either of the functions GENERAL
or DGENERAL
is used, you must supply explicit initial values for the parameters. By default, INIT=MODE. The following keywords are used:
-
MODE
-
uses the mode of the prior density as the initial value of the parameter, if you did not provide one. If the mode does not
exist or if it is on the boundary of the support of the density, the mean value is used. If the mean is outside of the support
or on the boundary, which can happen if the prior distribution is truncated, a random number drawn from the prior is used
as the initial value.
-
PINIT
-
tabulates parameter values after the tuning phase. This option also tabulates the tuned proposal parameters used by the Metropolis
algorithm. These proposal parameters include covariance matrices for continuous parameters and probability vectors for discrete
parameters for each block. By default, PROC MCMC does not display the initial values or the tuned proposal parameters after
the tuning phase.
-
RANDOM
-
generates a random number from the prior density and uses it as the initial value of the parameter, if you did not provide
one.
-
REINIT
-
resets the parameters, after the tuning phase, with the initial values that you provided explicitly or that were assigned
by PROC MCMC. By default, PROC MCMC does not reset the parameters because the tuning phase usually moves the Markov chains
to a more favorable place in the posterior distribution.
-
LIST
-
displays the model program and variable lists. The LIST option is a debugging feature and is not normally needed.
-
LISTCODE
-
displays the compiled program code. The LISTCODE option is a debugging feature and is not normally needed.
-
JOINTMODEL
JOINTLLIKE
-
specifies how the likelihood function is calculated. By default, PROC MCMC assumes that the observations in the data set are
independent so that the joint log-likelihood function is the sum of the individual log-likelihood functions for the observations,
where the individual log-likelihood function is specified in the MODEL
statement. When your data are not independent, you can specify the JOINTMODEL option to modify the way that PROC MCMC computes
the joint log-likelihood function. In this situation, PROC MCMC no longer steps through the input data set to sum the individual
log likelihood.
To use this option correctly, you need to do the following two things:
-
create ARRAY symbols to store all data set variables that are used in the program. This can be accomplished with the BEGINCNST
and ENDCNST
statements.
-
program the joint log-likelihood function by using these ARRAY symbols only. The MODEL
statement specifies the joint log-likelihood function for the entire data set. Typically, you use the function GENERAL
in the MODEL
statement.
See the sections BEGINCNST/ENDCNST Statement and Modeling Joint Likelihood for details.
-
MAXTUNE=n
-
specifies an upper limit for the number of proposal tuning loops. By default, MAXTUNE=24. See the section Covariance Tuning for more details.
-
MAXINDEXPRINT=number | ALL
MAXIPRINT=number | ALL
-
specifies the maximum number of observation indices to print in the ODS tables "Missing Response Information" table and "Missing
Covariates Information" table. This option applies only to programs that model missing data. The default value is 20. MAXINDEXPRINT=ALL
prints all observation indices for every missing variable that is modeled in PROC MCMC.
-
MAXSUBVALUEPRINT=number | ALL
MAXSVPRINT=number | ALL
-
specifies the maximum number of subject values to display in the "Subject Values" column of the ODS table "Random Effects
Parameters." This option applies only to programs that have RANDOM statements. The default value is 20. MAXSUBVALUEPRINT=ALL
prints all subject values for every random effect in the program.
-
MCHISTORY=keyword
MCHIST=keyword
-
controls the display of the Markov chain sampling history.
-
BRIEF
-
produces a summary output for the tuning, burn-in, and sampling history tables. The tables show the following when applicable:
-
“RWM Scale” shows the scale, or the range of the scales, used in each random walk Metropolis block that is normal or is based
on a t distribution.
-
“Probability” shows the proposal probability parameter, or the range of the parameters, used in each random walk Metropolis
block that is based on a geometric distribution.
-
“RWM Acceptance Rate” shows the acceptance rate, or the range of the acceptance rates, for each random walk Metropolis block.
-
“IM Acceptance Rate” shows the acceptance rate, or the range of the acceptance rates, for each independent Metropolis block.
-
DETAILED
-
produces detailed output of the tuning, burn-in, and sampling history tables, including scale values, acceptance probabilities,
blocking information, and so on. Use this option with caution, especially in random-effects models that have a large number
of random-effects groups. This option can produce copious output.
-
NONE
-
produces none of the tuning history, burn-in history, and sampling history tables.
The default is MCHISTORY=NONE.
-
MINTUNE=n
-
specifies a lower limit for the number of proposal tuning loops. By default, MINTUNE=2. See the section Covariance Tuning for more details.
-
MISSING=keyword
MISS=keyword
-
specifies how missing values are handled (see the section Handling of Missing Data for more details). The default is MISSING=COMPLETECASE.
-
ALLCASE | AC
-
gives you the option to model the missing values in an all-case analysis. You can use any techniques that you see fit, for
example, fully Bayesian or multiple imputation.
-
COMPLETECASE | CC
-
assumes a complete case analysis, so all observations with missing variable values are discarded prior to the simulation.
-
MONITOR= (symbol-list)
-
outputs analysis for selected symbols of interest in the program. The symbols can be any of the following: model parameters
(symbols in the PARMS
statement), secondary parameters (assigned using the operator "="), the log of the posterior density (LOGPOST), the log of
the prior density (LOGPRIOR), the log of the hyperprior density (LOGHYPER) if the HYPER
statement is used, or the log of the likelihood function (LOGLIKE). You can use the keyword _PARMS_ as a shorthand for all
of the model parameters. PROC MCMC performs only posterior analyses (such as plotting, diagnostics, and summaries) on the
symbols selected with the MONITOR= option. You can also choose to monitor an entire array by specifying the name of the array.
By default MONITOR=_PARMS_.
Posterior samples of any secondary parameters listed in the MONITOR= option are saved in the OUTPOST=
data set. Posterior samples of model parameters are always saved to the OUTPOST=
data set, regardless of whether they appear in the MONITOR= option.
-
NBI=n
-
specifies the number of burn-in iterations to perform before beginning to save parameter estimate chains. By default, NBI=1000.
See the section Burn-in, Thinning, and Markov Chain Samples in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details.
-
NMC=n
-
specifies the number of iterations in the main simulation loop. This is the MCMC sample size if THIN=1
. By default, NMC=1000.
-
NOLOGDIST
-
omits the calculation of the logarithm of the joint distribution of the model parameters at each iteration. The option applies
only if all parameters in the model are updated directly from their target distribution, either from the full conditional
posterior via conjugacy or from the marginal distribution. Such algorithms do not require the calculation of the joint posterior
distribution; hence PROC MCMC runs faster by avoiding these unnecessary calculations. As a result, the OUTPOST= data set does
not contain the LOGPRIOR, LOGLIKE, and LOGPOST variables.
-
NTHREADS=n
-
specifies the number of threads for simulation. PROC MCMC performs two types of threading. In sampling model parameters, PROC
MCMC allocates data to different threads and calculates the objective function by accumulating values from each thread; in
sampling of random-effects parameters and missing data variables, each thread generates a subset of these parameters simultaneously
at each iteration. Most sampling algorithms are threaded. NTHREADS=–1 sets the number of available threads to the number of
hyperthreaded cores available on the system. By default, NTHREADS=1.
-
NTU=n
-
specifies the number of iterations to use in each proposal tuning phase. By default, NTU=500.
-
OUTPOST=SAS-data-set
-
specifies an output data set that contains the posterior samples of all model parameters, the iteration numbers (variable
name ITERATION), the log of the posterior density (LOGPOST), the log of the prior density (LOGPRIOR), the log of the hyperprior
density (LOGHYPER), if the HYPER
statement is used, and the log likelihood (LOGLIKE). Any secondary parameters (assigned using the operator "=") listed in
the MONITOR=
option are saved to this data set. By default, no OUTPOST= data set is created.
-
PLOTS<(global-plot-options)>= (plot-request <… plot-request>)
PLOT<(global-plot-options)>= (plot-request <…plot-request>)
-
controls the display of diagnostic plots. Three types of plots can be requested: trace plots, autocorrelation function plots,
and kernel density plots. By default, the plots are displayed in panels unless the global plot option UNPACK is specified.
Also when more than one type of plot is specified, the plots are grouped by parameter unless the global plot option GROUPBY=TYPE
is specified. When you specify only one plot request, you can omit the parentheses around the plot-request, as shown in the
following example:
plots=none
plots(unpack)=trace
plots=(trace density)
ODS Graphics must be enabled before plots can be requested. For example:
ods graphics on;
proc mcmc data=exi seed=7 outpost=p1 plots=all;
parm mu;
prior mu ~ normal(0, sd=10);
model y ~ normal(mu, sd=1);
run;
ods graphics off;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
If ODS Graphics is enabled but you do not specify the PLOTS= option, then PROC MCMC produces, for each parameter, a panel
that contains the trace plot, the autocorrelation function plot, and the density plot. This is equivalent to specifying PLOTS=(TRACE
AUTOCORR DENSITY).
The global-plot-options include the following:
-
FRINGE
-
adds a fringe plot to the horizontal axis of the density plot.
-
GROUPBY|GROUP=PARAMETER | TYPE
-
specifies how the plots are grouped when there is more than one type of plot. GROUPBY=PARAMETER is the default. The choices
are as follows:
-
TYPE
-
specifies that the plots are grouped by type.
-
PARAMETER
-
specifies that the plots are grouped by parameter.
-
LAGS=n
-
specifies the number of autocorrelation lags used in plotting the ACF graph. By default, LAGS=50.
-
SMOOTH
-
smooths the trace plot with a fitted penalized B-spline curve (Eilers and Marx, 1996).
-
UNPACKPANEL
UNPACK
-
specifies that all paneled plots are to be unpacked, so that each plot in a panel is displayed separately.
The plot-requests are as follows:
-
ALL
-
requests all types of plots. PLOTS=ALL is equivalent to specifying PLOTS=(TRACE AUTOCORR DENSITY).
-
AUTOCORR | ACF
-
displays the autocorrelation function plots for the parameters.
-
DENSITY | D | KERNEL | K
-
displays the kernel density plots for the parameters.
-
NONE
-
suppresses the display of all plots.
-
TRACE | T
-
displays the trace plots for the parameters.
Consider a model with four parameters, X1–X4. Displays for various specifications are depicted as follows.
-
PLOTS=(TRACE AUTOCORR) displays the trace and autocorrelation plots for each parameter side by side with two parameters per
panel:
|
Display 1
|
Trace(X1)
|
Autocorr(X1)
|
| |
Trace(X2)
|
Autocorr(X2)
|
|
Display 2
|
Trace(X3)
|
Autocorr(X3)
|
| |
Trace(X4)
|
Autocorr(X4)
|
-
PLOTS(GROUPBY=TYPE)=(TRACE AUTOCORR) displays all the paneled trace plots, followed by panels of autocorrelation plots:
|
Display 1
|
Trace(X1)
|
| |
Trace(X2)
|
|
Display 2
|
Trace(X3)
|
| |
Trace(X4)
|
|
Display 3
|
Autocorr(X1)
|
Autocorr(X2)
|
| |
Autocorr(X3)
|
Autocorr(X4)
|
-
PLOTS(UNPACK)=(TRACE AUTOCORR) displays a separate trace plot and a separate correlation plot, parameter by parameter:
|
Display 1
|
Trace(X1)
|
|
Display 2
|
Autocorr(X1)
|
|
Display 3
|
Trace(X2)
|
|
Display 4
|
Autocorr(X2)
|
|
Display 5
|
Trace(X3)
|
|
Display 6
|
Autocorr(X3)
|
|
Display 7
|
Trace(X4)
|
|
Display 8
|
Autocorr(X4)
|
-
PLOTS(UNPACK GROUPBY=TYPE)=(TRACE AUTOCORR) displays all the separate trace plots followed by the separate autocorrelation
plots:
|
Display 1
|
Trace(X1)
|
|
Display 2
|
Trace(X2)
|
|
Display 3
|
Trace(X3)
|
|
Display 4
|
Trace(X4)
|
|
Display 5
|
Autocorr(X1)
|
|
Display 6
|
Autocorr(X2)
|
|
Display 7
|
Autocorr(X3)
|
|
Display 8
|
Autocorr(X4)
|
-
PROPCOV=value
-
specifies the method used in constructing the initial covariance matrix for the Metropolis-Hastings algorithm. The QUANEW
and NMSIMP methods find numerically approximated covariance matrices at the optimum of the posterior density function with
respect to all continuous parameters. The optimization does not apply to discrete parameters. The tuning phase starts at the
optimized values; in some problems, this can greatly increase convergence performance. If the approximated covariance matrix
is not positive definite, then an identity matrix is used instead. Valid values are as follows:
-
IND
-
uses the identity covariance matrix. This is the default. See the section Tuning the Proposal Distribution.
-
CONGRA<(optimize-options)>
-
performs a conjugate-gradient optimization.
-
DBLDOG<(optimize-options)>
-
performs a double-dogleg optimization.
-
QUANEW<(optimize-options)>
-
performs a quasi-Newton optimization.
-
NMSIMP | SIMPLEX<(optimize-options)>
-
performs a Nelder-Mead simplex optimization.
The optimize-options are as follows:
-
ITPRINT
-
prints optimization iteration steps and results.
-
PROPDIST=value
-
specifies a proposal distribution for the Metropolis algorithm. See the section Metropolis and Metropolis-Hastings Algorithms in Chapter 7: Introduction to Bayesian Analysis Procedures. You can also use PARMS
statement option (see the section PARMS Statement) to change the proposal distribution for a particular block of parameters. Valid values are as follows:
-
NORMAL
N
-
specifies a normal distribution as the proposal distribution. This is the default.
-
T<(df)>
-
specifies a t distribution with the degrees of freedom df. By default, df = 3. If df > 100, the normal distribution is used since the two distributions are almost identical.
-
REOBSINFO <(display-options)>
-
displays the ODS table "Random Effect Observation Information." The table lists the name of each random effect, the unique
values in the corresponding subject variable, the number of observations in each subject, and the observation indices for
each subject value.
To understand how this option works, consider the following statements:
data input;
array names{*} $ n1-n10 ("John" "Mary" "Chris" "Rob" "Greg"
"Jen" "Henry" "Alice" "James" "Toby");
call streaminit(17);
do i = 1 to 20;
j = ceil(rand("uniform") * 10 );
index = names[j];
output;
end;
drop n: j;
run;
proc print data=input;
run;
The input data set (Figure 61.11) contains the index variable, which indicates subjects in a hypothetical random-effects model.
Figure 61.11: Subject Variable in an Input Data Set
| 1 |
Mary |
| 2 |
James |
| 3 |
Mary |
| 4 |
Greg |
| 5 |
Chris |
| 6 |
James |
| 7 |
James |
| 8 |
Chris |
| 9 |
James |
| 10 |
James |
| 11 |
Chris |
| 12 |
Rob |
| 13 |
Rob |
| 14 |
Greg |
| 15 |
Greg |
| 16 |
Alice |
| 17 |
Jen |
| 18 |
Alice |
| 19 |
John |
| 20 |
Chris |
The following statements illustrate the use of the REOBSINFO option:
ods select reobsinfo;
proc mcmc data=input reobsinfo stats=none diag=none;
random u ~ normal(0, sd=1) subject=index;
model general(0);
run;
Figure 61.12 displays the "Random Effect Observation Information" table. The table contains the name of the random-effect parameter (u), the values of the subject variable index, the total number of observations, and the row index of these observations in each of the subject values.
Figure 61.12: Random Effect Observation Information
The MCMC Procedure
| Mary |
2 |
1 3 |
| James |
5 |
2 6 7 9 10 |
| Greg |
3 |
4 14 15 |
| Chris |
4 |
5 8 11 20 |
| Rob |
2 |
12 13 |
| Alice |
2 |
16 18 |
| Jen |
1 |
17 |
| John |
1 |
19 |
The display-options are as follows:
-
MAXVALUEPRINT=number | ALL
MAXVPRINT=number | ALL
-
prints the number of subject values for each random effect (that is, the number of rows that are displayed in the “Random
Effect Observation Information” table for each random effect). The default value is 20. MAXVALUEPRINT=ALL displays all subject
values.
-
MAXOBSPRINT=number | ALL
MAXOPRINT=number | ALL
-
prints the number of observation indices for each subject value of every random effect (that is, the maximum number of indices
that are displayed in the “Observation Indices” column in the “Random Effect Observation Information” table). The default
value is 20. MAXOBSPRINT=ALL displays indices for every subject value.
-
SCALE=value
-
controls the initial multiplicative scale to the covariance matrix of the proposal distribution. By default, SCALE=2.38. See
the section Scale Tuning for more details.
-
SEED=n
-
specifies the random number seed. By default, SEED=0, and PROC MCMC gets a random number seed from the clock.
-
SIMREPORT=n
-
controls the number of times that PROC MCMC reports the expected run time of the simulation. This can be useful for monitoring
the progress of CPU-intensive programs. For example, with SIMREPORT=2, PROC MCMC reports the simulation progress twice. By
default, SIMREPORT=0, and there is no reporting. The expected run times are displayed in the log file.
-
SINGDEN=value
-
defines the singularity criterion in PROC MCMC. By default, SINGDEN=1E-11. The value indicates the exclusion of an endpoint in an interval. The mathematical notation "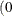 " is equivalent to "
" is equivalent to "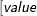 " in PROC MCMC—that is,
" in PROC MCMC—that is, 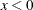 is treated as
is treated as 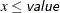 in PROC MCMC. The maximum SINGDEN allowed is 1E-6.
in PROC MCMC. The maximum SINGDEN allowed is 1E-6.
-
STATISTICS<(global-stats-options)> = NONE | ALL |stats-request
STATS<(global-stats-options)> = NONE | ALL |stats-request
-
specifies options for posterior statistics. By default, PROC MCMC computes the posterior mean, standard deviation, quantiles,
and two 95% credible intervals: equal-tail and highest posterior density (HPD). Other available statistics include the posterior
correlation and covariance. See the section Summary Statistics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details. You can request all of the posterior statistics by specifying STATS=ALL. You can suppress all the calculations
by specifying STATS=NONE.
You can use postprocessing autocall macros to calculate posterior summary statistics of the posterior samples after PROC MCMC
has exited. See the section Autocall Macros for Postprocessing.
The global-stats-options includes the following:
-
ALPHA=numeric-list
-
specifies the  level for the equal-tail and HPD intervals. The value
level for the equal-tail and HPD intervals. The value  must be between 0 and 0.5. By default, ALPHA=0.05.
must be between 0 and 0.5. By default, ALPHA=0.05.
-
PERCENTAGE | PERCENT=numeric-list
-
calculates the posterior percentages. The numeric-list contains values between 0 and 100. By default, PERCENTAGE=(25 50 75).
The stats-requests include the following:
-
ALL
-
computes all posterior statistics. You can combine the option ALL with any other options. For example STATS(ALPHA=(0.02 0.05
0.1))=ALL computes all statistics with the default settings and intervals at  levels of 0.02, 0.05, and 0.1.
levels of 0.02, 0.05, and 0.1.
-
CORR
-
computes the posterior correlation matrix.
-
COV
-
computes the posterior covariance matrix.
-
SUMMARY
SUM
-
computes the posterior means, standard deviations, and percentile points for each variable. By default, the 25th, 50th, and
75th percentile points are produced, but you can use the global PERCENT= option to request specific percentile points.
-
INTERVAL
INT
-
computes the 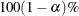 equal-tail and HPD credible intervals for each variable. See the sections Equal-Tail Credible Interval in Chapter 7: Introduction to Bayesian Analysis Procedures, and Highest Posterior Density (HPD) Interval in Chapter 7: Introduction to Bayesian Analysis Procedures, for details. By default, ALPHA=0.05, but you can use the global ALPHA= option to request other intervals of any probabilities.
equal-tail and HPD credible intervals for each variable. See the sections Equal-Tail Credible Interval in Chapter 7: Introduction to Bayesian Analysis Procedures, and Highest Posterior Density (HPD) Interval in Chapter 7: Introduction to Bayesian Analysis Procedures, for details. By default, ALPHA=0.05, but you can use the global ALPHA= option to request other intervals of any probabilities.
-
NONE
-
suppresses all of the statistics.
-
TARGACCEPT=value
-
specifies the target acceptance rate for the random walk based Metropolis algorithm. See the section Metropolis and Metropolis-Hastings Algorithms in Chapter 7: Introduction to Bayesian Analysis Procedures. The numeric value must be between 0.01 and 0.99. By default, TARGACCEPT=0.45 for models with 1 parameter; TARGACCEPT=0.35 for models with 2,
3, or 4 parameters; and TARGACCEPT=0.234 for models with more than 4 parameters (Roberts, Gelman, and Gilks; 1997; Roberts and Rosenthal; 2001).
-
TARGACCEPTI=value
-
specifies the target acceptance rate for the independence sampler algorithm. The independence sampler is used for blocks of
binary parameters. See the section Independence Sampler in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details. The numeric value must be between 0 and 1. By default, TARGACCEPTI=0.6.
-
THIN=n
NTHIN=n
-
controls the thinning rate of the simulation. PROC MCMC keeps every nth simulation sample and discards the rest. All of the posterior statistics and diagnostics are calculated using the thinned
samples. By default, THIN=1. See the section Burn-in, Thinning, and Markov Chain Samples in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details.
-
TRACE
-
displays the result of each operation in each statement in the model program as it is executed. This debugging option is very
rarely needed, and it produces voluminous output. If you use this option, also use small NMC=, NBI=, MAXTUNE=, and NTU= numbers.
-
TUNEWT=value
-
specifies the multiplicative weight used in updating the covariance matrix of the proposal distribution. The numeric value must be between 0 and 1. By default, TUNEWT=0.75. See the section Covariance Tuning for more details.



 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics