The MCMC Procedure

Simple Linear Regression

This section illustrates some basic features of PROC MCMC by using a linear regression model. The model is as follows:

$Y_ i = \beta _0 + \beta _1 X_ i + \epsilon _ i$

for the observations $i=1,2,\ldots ,n$ .

The following statements create a SAS data set with measurements of Height and Weight for a group of children:

title 'Simple Linear Regression';

data Class;
   input Name $ Height Weight @@;
   datalines;
Alfred  69.0 112.5   Alice  56.5  84.0   Barbara 65.3  98.0
Carol   62.8 102.5   Henry  63.5 102.5   James   57.3  83.0
Jane    59.8  84.5   Janet  62.5 112.5   Jeffrey 62.5  84.0
John    59.0  99.5   Joyce  51.3  50.5   Judy    64.3  90.0
Louise  56.3  77.0   Mary   66.5 112.0   Philip  72.0 150.0
Robert  64.8 128.0   Ronald 67.0 133.0   Thomas  57.5  85.0
William 66.5 112.0
;

The equation of interest is as follows:

$\mbox{Weight}_ i = \beta _0 + \beta _1 \mbox{Height}_ i + \epsilon _ i$

The observation errors, $\epsilon _ i$ , are assumed to be independent and identically distributed with a normal distribution with mean zero and variance $\sigma ^2$ .

$\mbox{Weight}_ i \sim \mbox{normal}(\beta _0 + \beta _1 \mbox{Height}_ i, \sigma ^2)$

The likelihood function for each of the Weight, which is specified in the MODEL statement, is as follows:

$p(\mbox{Weight} | \beta _0, \beta _1, \sigma ^2, \mbox{Height}_ i) = \phi (\beta _0 + \beta _1 \mbox{Height}_ i, \sigma ^2)$

where $p(\cdot | \cdot )$ denotes a conditional probability density and $\phi$ is the normal density. There are three parameters in the likelihood: $\beta _0$ , $\beta _1$ , and $\sigma ^2$ . You use the PARMS statement to indicate that these are the parameters in the model.

Suppose you want to use the following three prior distributions on each of the parameters:

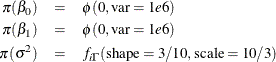
$\begin{eqnarray*} \pi (\beta _0) & =& \phi (0, \mbox{var}=1e6) \\ \pi (\beta _1) & =& \phi (0, \mbox{var}=1e6) \\ \pi (\sigma ^2) & =& f_{i\Gamma }(\mbox{shape}=3/10, \mbox{scale}=10/3) \end{eqnarray*}$

where $\pi (\cdot )$ indicates a prior distribution and $f_{i\Gamma }$ is the density function for the inverse-gamma distribution. The normal priors on $\beta _0$ and $\beta _1$ have large variances, expressing your lack of knowledge about the regression coefficients. The priors correspond to an equal-tail 95% credible intervals of approximately (-2000, 2000) for $\beta _0$ and $\beta _1$ . Priors of this type are often called vague or diffuse priors. See the section Prior Distributions in Chapter 7: Introduction to Bayesian Analysis Procedures, for more information. Typically diffuse prior distributions have little influence on the posterior distribution and are appropriate when stronger prior information about the parameters is not available.

A frequently used prior for the variance parameter $\sigma ^2$ is the inverse-gamma distribution. See Table 61.22 in the section Standard Distributions for the density definition. The inverse-gamma distribution is a conjugate prior (see the section Conjugate Sampling) for the variance parameter in a normal distribution. Also see the section Gamma and Inverse-Gamma Distributions for typical usages of the gamma and inverse-gamma prior distributions. With a shape parameter of 3/10 and a scale parameter of 10/3, this prior corresponds to an equal-tail 95% credible interval of (1.7, 1E6), with the mode at 2.5641 for $\sigma ^2$ . Alternatively, you can use any other prior distribution with positive support on this variance component. For example, you can use the gamma prior.

According to Bayes’ theorem, the likelihood function and prior distributions determine the posterior (joint) distribution of $\beta _0$ , $\beta _1$ , and $\sigma ^2$ as follows:

$\begin{eqnarray*} \pi (\beta _0, \beta _1, \sigma ^2 | \mbox{Weight}, \mbox{Height}) & \propto & \pi (\beta _0) \pi (\beta _1) \pi (\sigma ^2) p(\mbox{Weight} | \beta _0, \beta _1, \sigma ^2, \mbox{Height}) \end{eqnarray*}$

You do not need to know the form of the posterior distribution when you use PROC MCMC. PROC MCMC automatically obtains samples from the desired posterior distribution, which is determined by the prior and likelihood you supply.

The following statements fit this linear regression model with diffuse prior information:

ods graphics on;
proc mcmc data=class outpost=classout nmc=10000 thin=2 seed=246810;
   parms beta0 0 beta1 0;
   parms sigma2 1;
   prior beta0 beta1 ~ normal(mean = 0, var = 1e6);
   prior sigma2 ~ igamma(shape = 3/10, scale = 10/3);
   mu = beta0 + beta1*height;
   model weight ~ n(mu, var = sigma2);
run;
ods graphics off;

When ODS Graphics is enabled, diagnostic plots, such as the trace and autocorrelation function plots of the posterior samples, are displayed. For more information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS.

The PROC MCMC statement invokes the procedure and specifies the input data set Class. The output data set Classout contains the posterior samples for all of the model parameters. The NMC= option specifies the number of posterior simulation iterations. The THIN= option controls the thinning of the Markov chain and specifies that one of every 2 samples is kept. Thinning is often used to reduce the correlations among posterior sample draws. In this example, 5,000 simulated values are saved in the Classout data set. The SEED= option specifies a seed for the random number generator, which guarantees the reproducibility of the random stream. For more information about Markov chain sample size, burn-in, and thinning, see the section Burn-in, Thinning, and Markov Chain Samples in Chapter 7: Introduction to Bayesian Analysis Procedures.

The PARMS statements identify the three parameters in the model: beta0, beta1, and sigma2. Each statement also forms a block of parameters, where the parameters are updated simultaneously in each iteration. In this example, beta0 and beta1 are sampled jointly, conditional on sigma2; and sigma2 is sampled conditional on fixed values of beta0 and beta1. In simple regression models such as this, you expect the parameters beta0 and beta1 to have high posterior correlations, and placing them both in the same block improves the mixing of the chain—that is, the efficiency that the posterior parameter space is explored by the Markov chain. For more information, see the section Blocking of Parameters. The PARMS statements also assign initial values to the parameters (see the section Initial Values of the Markov Chains). The regression parameters are given 0 as their initial values, and the scale parameter sigma2 starts at value 1. If you do not provide initial values, PROC MCMC chooses starting values for every parameter.

The PRIOR statements specify prior distributions for the parameters. The parameters beta0 and beta1 both share the same prior—a normal prior with mean 0 and variance 1e6. The parameter sigma2 has an inverse-gamma distribution with a shape parameter of 3/10 and a scale parameter of 10/3. For a list of standard distributions that PROC MCMC supports, see the section Standard Distributions.

The MU assignment statement calculates the expected value of Weight as a linear function of Height. The MODEL statement uses the shorthand notation, n, for the normal distribution to indicate that the response variable, Weight, is normally distributed with parameters mu and sigma2. The functional argument MEAN= in the normal distribution is optional, but you have to indicate whether sigma2 is a variance (VAR=), a standard deviation (SD=), or a precision (PRECISION=) parameter. See Table 61.2 in the section MODEL Statement for distribution specifications.

The distribution parameters can contain expressions. For example, you can write the MODEL statement as follows:

model weight ~ n(beta0 + beta1*height, var = sigma2);

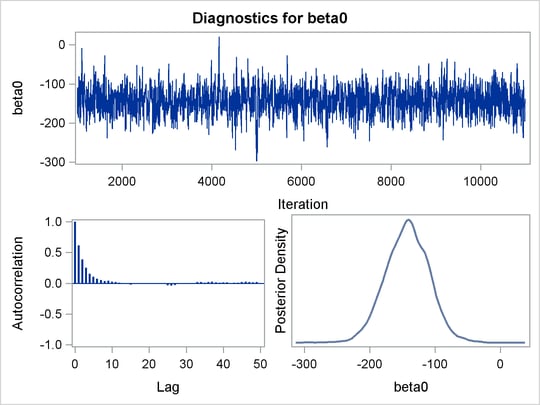
Before you do any posterior inference, it is essential that you examine the convergence of the Markov chain (see the section Assessing Markov Chain Convergence in Chapter 7: Introduction to Bayesian Analysis Procedures). You cannot make valid inferences if the Markov chain has not converged. A very effective convergence diagnostic tool is the trace plot. Although PROC MCMC produces graphs at the end of the procedure output (see Figure 61.5), you should visually examine the convergence graph first.

The first table that PROC MCMC produces is the "Number of Observations" table, as shown in Figure 61.1. This table lists the number of observations read from the DATA= data set and the number of observations used in the analysis.

Figure 61.1: Observation Information

Simple Linear Regression

The MCMC Procedure

Number of Observations Read

Number of Observations Used

The "Parameters" table, shown in Figure 61.2, lists the names of the parameters, the blocking information, the sampling method used, the starting values, and the prior distributions. For more information about blocking information, see the section Blocking of Parameters; for more information about starting values, see the section Initial Values of the Markov Chains. The first block, which consists of the parameters beta0 and beta1, uses a random walk Metropolis algorithm. The second block, which consists of the parameter sigma2, is updated via its full conditional distribution in conjugacy. You should check this table to ensure that you have specified the parameters correctly, especially for complicated models.

Figure 61.2: Parameter Information

Parameters
Block	Parameter	Sampling Method	Initial Value	Prior Distribution
1	beta0	N-Metropolis	0	normal(mean = 0, var = 1e6)
	beta1		0	normal(mean = 0, var = 1e6)
2	sigma2	Conjugate	1.0000	igamma(shape = 3/10, scale = 10/3)

For each posterior distribution, PROC MCMC also reports summary and interval statistics (posterior means, standard deviations, and 95% highest posterior density credible intervals), as shown in Figure 61.3. For more information about posterior statistics, see the section Summary Statistics in Chapter 7: Introduction to Bayesian Analysis Procedures.

Figure 61.3: MCMC Summary and Interval Statistics

Simple Linear Regression

The MCMC Procedure

Posterior Summaries and Intervals
Parameter	N	Mean	Standard Deviation	95% HPD Interval
beta0	5000	-142.8	33.4326	-210.8	-81.6714
beta1	5000	3.8924	0.5333	2.9056	4.9545
sigma2	5000	137.3	51.1030	59.2362	236.3

By default, PROC MCMC computes the effective sample sizes (ESSs) as a convergence diagnostic test to help you determine whether the chain has converged. The ESSs are shown in Figure 61.4. For details and interpretations of ESS and additional convergence diagnostics, see the section Assessing Markov Chain Convergence in Chapter 7: Introduction to Bayesian Analysis Procedures.

Figure 61.4: MCMC Convergence Diagnostics

Simple Linear Regression

The MCMC Procedure

Effective Sample Sizes
Parameter	ESS	Autocorrelation Time	Efficiency
beta0	1102.2	4.5366	0.2204
beta1	1119.0	4.4684	0.2238
sigma2	2910.1	1.7182	0.5820

PROC MCMC produces a number of graphs, shown in Figure 61.5, which also aid convergence diagnostic checks. With the trace plots, there are two important aspects to examine. First, you want to check whether the mean of the Markov chain has stabilized and appears constant over the graph. Second, you want to check whether the chain has good mixing and is "dense," in the sense that it quickly traverses the support of the distribution to explore both the tails and the mode areas efficiently. The plots show that the chains appear to have reached their stationary distributions.

Next, you should examine the autocorrelation plots, which indicate the degree of autocorrelation for each of the posterior samples. High correlations usually imply slow mixing. Finally, the kernel density plots estimate the posterior marginal distributions for each parameter.

Figure 61.5: Diagnostic Plots for $\beta _0$ , $\beta _1$ and $\sigma ^2$

In regression models such as this, you expect the posterior estimates to be very similar to the maximum likelihood estimators with noninformative priors on the parameters, The REG procedure produces the following fitted model (code not shown):

$\mbox{Weight} = -143.0 + 3.9 \times \mbox{Height}$

These are very similar to the means show in Figure 61.3. With PROC MCMC, you can carry out informative analysis that uses specifications to indicate prior knowledge on the parameters. Informative analysis is likely to produce different posterior estimates, which are the result of information from both the likelihood and the prior distributions. Incorporating additional information in the analysis is one major difference between the classical and Bayesian approaches to statistical inference.