The MCMC Procedure

Standard Distributions

Subsections:

The section Univariate Distributions (Table 61.7 through Table 61.35) lists all univariate distributions that PROC MCMC recognizes. The section Multivariate Distributions (Table 61.36 through Table 61.40) lists all multivariate distributions that PROC MCMC recognizes. With the exception of the multinomial distribution, all these distributions can be used in the MODEL , PRIOR , and HYPERPRIOR statements. The multinomial distribution is supported only in the MODEL statement. The RANDOM statement supports a limited number of distributions; see Table 61.4 for the complete list.

See the section Using Density Functions in the Programming Statements for information about how to use distributions in the programming statements. To specify an arbitrary distribution, you can use the GENERAL and DGENERAL functions. See the section Specifying a New Distribution for more details. See the section Truncation and Censoring for tips about how to work with truncated distributions and censoring data.

Univariate Distributions

Table 61.7: Beta Distribution

PROC specification

beta(a, b)

Density

$\frac{\Gamma (a+b)}{\Gamma (a) \Gamma (b)} \theta ^{a-1} (1-\theta )^{b-1}$

Parameter restriction

$a > 0$, $ b > 0 $

Range

$ \left\{ \begin{array}{ll} \left[ 0, 1 \right] & \mbox{when } a = 1, b = 1 \\ \left[ 0, 1 \right) & \mbox{when } a = 1, b \neq 1 \\ \left( 0, 1 \right] & \mbox{when } a \neq 1, b = 1 \\ \left( 0, 1 \right) & \mbox{otherwise} \end{array} \right. $

Mean

$\frac{a}{a+b}$

Variance

$ \frac{ab}{(a+b)^2(a+b+1)}$

Mode

$ \left\{ \begin{array}{ll} \frac{a-1}{a+b-2} & a > 1, b > 1 \\ 0 \mbox{ and } 1 & a < 1, b < 1 \\ 0 & \left\{ \begin{array}{l} a < 1, b \geq 1 \\ a = 1, b > 1 \\ \end{array} \right. \\ 1 & \left\{ \begin{array}{l} a \geq 1, b < 1 \\ a > 1, b = 1 \\ \end{array} \right. \\ \mbox{does not exist uniquely} & a = b = 1 \end{array} \right. $

Random number

If $\min (a,b) > 1 $, see (Cheng, 1978); if $\max (a, b) < 1$, see (Atkinson and Whittaker, 1976) and (Atkinson, 1979); if $\min (a, b) < 1$ and $\max (a, b) > 1$, see (Cheng, 1978); if a = 1 or b = 1, use the inversion method; if $ a = b = 1 $, use a uniform random number generator.


Table 61.8: Binary Distribution

PROC specification

binary(p)

Density

$p^\theta (1-p)^{1-\theta }$

Parameter restriction

$ 0 \leq p \leq 1 $

Range

$ \left\{ \begin{array}{ll} \{ 0\} & \mbox{when } p = 0 \\ \{ 1\} & \mbox{when } p = 1 \\ \{ 0, 1 \} & \mbox{otherwise} \end{array} \right. $

Mean

round$(p) $

Variance

$p(1-p)$

Mode

$ \left\{ \begin{array}{ll} \{ 1\} & \mbox{when } p = 1 \\ \{ 0\} & \mbox{otherwise} \end{array} \right. $

Random number

Generate $u \sim \mbox{uniform}(0, 1)$. If $ u \leq p$, $ \theta = 1$; else, $ \theta = 0. $


Table 61.9: Binomial Distribution

PROC specification

binomial(n, p)

Density

$\left(\begin{array}{l} n \\ \theta \end{array} \right) p^\theta (1-p)^{n-\theta }$

Parameter restriction

$ n = {0, 1, 2, \cdots } \; 0 \leq p \leq 1 $

Range

$ \theta \in \{ 0, \cdots , n \} $

Mean

$\lfloor np \rfloor $

Variance

$np(1-p)$

Mode

$\lfloor (n+1)p \rfloor $


Table 61.10: Cauchy Distribution

PROC specification

cauchy(a, b)

Density

$ \frac{1}{\pi } \left( \frac{b}{b^2 + (\theta -a)^2} \right) $

Parameter restriction

$ b > 0 $

Range

$ \theta \in (-\infty , \infty ) $

Mean

Does not exist.

Variance

Does not exist.

Mode

a

Random number

Generate $u_1, u_2 \sim \mbox{uniform}(0, 1)$; let $v = 2u_2 - 1 $. Repeat the procedure until $u_1^2 + v^2 < 1 $. $y = v/u_1 $ is a draw from the standard Cauchy, and $\theta = a+by$ (Ripley, 1987).


Table 61.11: $\chi ^2$ Distribution

PROC specification

chisq($\nu $)

Density

$ \frac{1}{\Gamma (\nu /2) 2^{\nu /2}} \theta ^{(\nu /2)-1} e^{-\theta /2} $

Parameter restriction

$ \nu > 0 $

Range

$ \theta \in [0, \infty ) $ if $\nu = 2$; $(0, \infty )$ otherwise.

Mean

$ \nu $

Variance

$ 2\nu $

Mode

$ \nu - 2 $ if $\nu \geq 2$; does not exist otherwise.

Random number

$\chi ^2$ is a special case of the gamma distribution: $ \theta \sim \mbox{gamma}(\nu /2, \mbox{scale=} 2) $ is a draw from the $\chi ^2$ distribution.


Table 61.12: Exponential $\chi ^2$ Distribution

PROC specification

expchisq($\nu $)

Density

$\frac{1}{\Gamma ( \nu /2) 2^{\nu /2}} \exp ( \theta )^{\nu /2}\exp ( -\exp ( \theta ) /2 ) $

Parameter restriction

$ \nu > 0 $

Range

$ \theta \in (-\infty , \infty ) $

Mode

$ \log (\nu ) $

Random number

Generate $x_1 \sim \chi ^2(\nu ) $, and $\theta = \log (x_1)$ is a draw from the exponential $\chi ^2$ distribution.

Relationship to the $\chi ^2$ distribution

$\theta \sim \chi ^2(\nu ) \Leftrightarrow \log (\theta ) \sim \exp \chi ^2(\nu )$


Table 61.13: Exponential Exponential Distribution

PROC specification

expexpon(scale = b )

expexpon(iscale = $\beta $ )

Density

$\frac{1}{b}\exp ( \theta ) \exp (-\exp (\theta ) /b) $

$\beta \exp (\theta ) \exp (-\exp ( \theta ) \cdot \beta ) $

Parameter restriction

$b > 0 $

$\beta > 0 $

Range

$ \theta \in (-\infty , \infty )$

Same

Mode

$ \log (b)$

$ \log (1/\beta )$

Random number

Generate $x_1 \sim \mbox{expon}(\mbox{scale=} b) $, and $\theta = \log (x_1)$ is a draw from the exponential exponential distribution. Note that an exponential exponential distribution is not the same as the double exponential distribution.

Relationship to the exponential distribution

$\theta \sim \mbox{expon}(b) \Leftrightarrow \log (\theta ) \sim \mbox{expExpon}(b)$


Table 61.14: Exponential Gamma Distribution

PROC specification

expgamma(a, scale = b )

expgamma(a, iscale = $\beta $ )

Density

$\frac{1}{b^{a}\Gamma (a)} e^{a \theta } \exp (-e^{\theta } /b ) $

$ \frac{\beta ^{a}}{\Gamma (a) } e^{a \theta } \exp ( - e^{\theta } \cdot \beta ) $

Parameter restriction

$ a > 0, b > 0 $

$ a > 0, \beta > 0 $

Range

$ \theta \in (-\infty , \infty )$

Same

Mode

$ \log (ab)$

$ \log (a/\beta )$

Random number

Generate $x_1 \sim \mbox{gamma}(a, \mbox{scale} = b) $, and $\theta = \log (x_1)$ is a draw from the exponential gamma distribution.

Relationship to the $\Gamma $ distribution

$\theta \sim \mbox{gamma}(a, b) \Leftrightarrow \log (\theta ) \sim \mbox{expGamma}(a, b)$


Table 61.15: Exponential Inverse $\chi ^2$ Distribution

PROC specification

expichisq($\nu $)

Density

$\frac{1}{\Gamma ( \frac{\nu }{2}) 2^{\nu /2}}\exp ( -\nu \theta / 2 ) \exp ( -1/(2\exp ( \theta ) )) $

Parameter restriction

$ \nu > 0 $

Range

$ \theta \in (-\infty , \infty ) $

Mode

$ -\log (\nu ) $

Random number

Generate $x_1 \sim i\chi ^2(\nu ) $, and $\theta = \log (x_1)$ is a draw from the exponential inverse $\chi ^2$ distribution.

Relationship to the $i\chi ^2$ distribution

$\theta \sim i\chi ^2(\nu ) \Leftrightarrow \log (\theta ) \sim \exp i\chi ^2(\nu )$


Table 61.16: Exponential Inverse-Gamma Distribution

PROC specification

expigamma(a, scale = b )

expigamma(a, iscale = $\beta $ )

Density

$\frac{b^{a}}{\Gamma (a) } \exp ( -\alpha \theta ) \exp ( -b/\exp ( \theta ) ) $

$\frac{1}{\beta ^{\alpha }\Gamma ( a) } \exp ( -\alpha \theta ) \exp ( -\frac{1}{ \beta \exp ( \theta ) }) $

Parameter restriction

$ a > 0, b > 0 $

$ a > 0, \beta > 0 $

Range

$ \theta \in (-\infty , \infty )$

Same

Mode

$ -\log (a/b)$

$ -\log (a\beta )$

Random number

Generate $x_1 \sim \mbox{igamma}(a, \mbox{scale} = b) $, and $\theta = \log (x_1)$ is a draw from the exponential inverse-gamma distribution.

Relationship to the $i\Gamma $ distribution

$\theta \sim \mbox{igamma}(a, b) \Leftrightarrow \log (\theta ) \sim \mbox{eigamma}(a, b)$


Table 61.17: Exponential Scaled Inverse $\chi ^2$ Distribution

PROC specification

expsichisq($\nu $, s)

Density

$\frac{ (\frac{\nu }{2}) ^{\nu /2}}{ \Gamma ( \frac{\nu }{2}) }s^{\nu }\exp (-\nu \theta /2) \exp ( -\nu s^{2}/(2\exp (\theta ))) $

Parameter restriction

$ \nu > 0, s > 0 $

Range

$ \theta \in (-\infty , \infty ) $

Mode

$ \log (s^2) $

Random number

Generate $x_1 \sim si\chi ^2(\nu , s) $, and $\theta = \log (x_1)$ is a draw from the exponential scaled inverse $\chi ^2$ distribution.

Relationship to the $si\chi ^2$ distribution

$\theta \sim si\chi ^2(\nu , s) \Leftrightarrow \log (\theta ) \sim \exp si\chi ^2(\nu , s)$


Table 61.18: Exponential Distribution

PROC specification

expon(scale = b )

expon(iscale = $\beta $ )

Density

$\frac{1}{b} e^{-\theta /b} $

$\beta e^{-\beta \theta } $

Parameter restriction

$ b > 0 $

$\beta > 0 $

Range

$ \theta \in [0, \infty ) $

Same

Mean

b

$1/\beta $

Variance

$b^2$

$1/\beta ^2$

Mode

0

0

Random number

The exponential distribution is a special case of the gamma distribution: $\theta \sim \mbox{gamma}(1, \mbox{scale} = b)$ is a draw from the exponential distribution.


Table 61.19: Gamma Distribution

PROC specification

gamma(a, scale = b )

gamma(a, iscale = $\beta $ )

Density

$\frac{1}{b^ a\Gamma (a)} \theta ^{a-1} e^{-\theta /b} $

$\frac{\beta ^ a}{\Gamma (a)} \theta ^{a-1} e^{-\beta \theta } $

Parameter restriction

$ a > 0, b > 0 $

$ a > 0, \beta > 0 $

Range

$ \theta \in [0, \infty )$ if $a=1; (0, \infty )$ otherwise.

Same

Mean

ab

$a/\beta $

Variance

$ab^2$

$a/\beta ^2$

Mode

$ (a-1)b$ if $a \geq 1$

$ (a-1)/\beta $ if $a \geq 1$

Random number

See (McGrath and Irving, 1973).


Table 61.20: Geometric Distribution

PROC specification

geo(p)

Density *

$ p(1-p)^\theta $

Parameter restriction

$ 0 < p \leq 1 $

Range

$ \theta \in \left\{ \begin{array}{ll} \{ 0, 1, 2, \ldots \} & 0 < p < 1 \\ \{ 0\} & p = 1 \\ \end{array} \right. $

Mean

round($\frac{1-p}{p}$)

Variance

$\frac{1-p}{p^2}$

Mode

0

Random number

Based on samples obtained from a Bernoulli distribution with probability p until the first success.

*The random variable $\theta $ is the total number of failures in an experiment before the first success. This density function is not to be confused with another popular formulation, $p (1-p)^{\theta -1}$, which counts the total number of trials until the first success.


Table 61.21: Inverse $\chi ^2$ Distribution

PROC specification

ichisq($\nu $)

Density

$ \frac{1}{\Gamma (\nu /2) 2^{\nu /2}} \theta ^{-(\nu /2+1)} e^{-1/(2\theta )} $

Parameter restriction

$ \nu > 0 $

Range

$ \theta \in (0, \infty ) $

Mean

$ \frac{1}{\nu -2} $ if $\nu > 2$

Variance

$ \frac{2}{(\nu -2)^2(\nu -4)} $ if $\nu > 4$

Mode

$ \frac{1}{\nu + 2} $

Random number

Inverse $\chi ^2$ is a special case of the inverse-gamma distribution: $ \theta \sim \mbox{igamma}( \nu /2, \mbox{iscale} = 2) $ is a draw from the inverse $\chi ^2$ distribution.


Table 61.22: Inverse-Gamma Distribution

PROC specification

igamma(a, scale = b )

igamma(a, iscale = $\beta $ )

Density

$ \frac{b^ a}{\Gamma (a)} \theta ^{-(a+1)} e^{-b/\theta } $

$ \frac{1}{\beta ^ a \Gamma (a)} \theta ^{-(a+1)} e^{-1/\beta \theta } $

Parameter restriction

$ a > 0, b > 0 $

$ a > 0, \beta > 0 $

Range

$ \theta \in (0, \infty ) $

Same

Mean

$ \frac{b}{a-1}$ if $ a > 1$

$ \frac{1}{\beta (a-1)}$ if $ a > 1$

Variance

$ \frac{b^2}{(a-1)^2(a-2)}$

$ \frac{1}{\beta ^2(a-1)^2(a-2)}$

Mode

$ \frac{b}{a+1} $

$ \frac{1}{\beta (a+1)} $

Random number

Generate $x_1 \sim \mbox{gamma}(a, \mbox{scale} = b) $, and $\theta = 1/x_1$ is a draw from the $\mbox{igamma}(a, \mbox{iscale} = b)$ distribution.

Relationship to the gamma distribution

$\theta \sim \mbox{gamma}(a, \mbox{iscale} = b) \Leftrightarrow 1/\theta \sim \mbox{igamma}(a, \mbox{scale} = b)$


Table 61.23: Laplace (Double Exponential) Distribution

PROC specification

laplace(a, scale = b)

laplace(a, iscale = $\beta $)

Density

$\frac{1}{2b} e^{-|\theta -a|/b}$

$\frac{\beta }{2} e^{-\beta |\theta -a|}$

Parameter restriction

$ b > 0 $

$ \beta > 0$

Range

$ \theta \in (-\infty , \infty ) $

Same

Mean

a

a

Variance

$ 2b^2 $

$ 2 / \beta ^2 $

Mode

a

a

Random number

Inverse CDF. $ F(\theta ) = \left\{ \begin{array}{ll} \frac{1}{2} \exp \left( -\frac{a-\theta }{b}\right) & \theta < a \\ 1 - \frac{1}{2} \exp \left( -\frac{\theta - a}{b}\right) & \theta \geq a \end{array} \right. . $ Generate $u_1, u_2 \sim \mbox{uniform}(0, 1) $. If $u_1 < 0.5, \theta = a + b\log (u_2);$ else $ \theta = a - b \log (u_2) $. $\theta $ is a draw from the Laplace distribution.


Table 61.24: Logistic Distribution

PROC specification

logistic(a, b)

Density

$ \frac{\exp \left(-\frac{\theta -a}{b} \right)}{b \left(1+\exp \left( -\frac{\theta -a}{b} \right) \right)^2} $

Parameter restriction

$ b > 0 $

Range

$ \theta \in (-\infty , \infty ) $

Mean

a

Variance

$ \frac{\pi ^2 b^2}{3}$

Mode

a

Random number

Inverse CDF method with $F(\theta ) = \left(1 + \exp (-\frac{\theta - a}{b}) \right)^{-1} $. Generate $u \sim \mbox{uniform}(0,1)$, and $\theta = a - b\log (1/u-1) $ is a draw from the logistic distribution.


Table 61.25: Lognormal Distribution

PROC specification

lognormal($\mu $, sd = s)

lognormal($\mu $, var = v)

lognormal($\mu $, prec = $\tau $)

Density

$ \frac{1}{\theta s\sqrt {2\pi }} \exp \left( - \frac{(\log {\theta } - \mu )^2}{2s^2} \right) $

$ \frac{1}{\theta \sqrt {2\pi v}} \exp \left( - \frac{(\log {\theta } - \mu )^2}{2v} \right) $

$ \frac{1}{\theta } \sqrt {\frac{\tau }{2\pi }} \exp \left( - \frac{\tau (\log {\theta } - \mu )^2}{2} \right) $

Parameter restriction

$ s > 0 $

$ v > 0 $

$ \tau > 0 $

Range

$ \theta \in (0, \infty ) $

Same

Same

Mean

$ \exp (\mu + s^2/2) $

$ \exp (\mu + v/2) $

$ \exp (\mu + 1/(2\tau )) $

Variance

$ \begin{array}{l} \exp {(2(\mu +s^2))} \\ - \exp {(2\mu +s^2)} \end{array} $

$ \begin{array}{l} \exp {(2(\mu +v))} \\ - \exp {(2\mu +v)} \end{array} $

$ \begin{array}{l} \exp {(2(\mu +1/\tau ))} \\ - \exp {(2\mu +1/\tau )} \end{array} $

Mode

$ \exp (\mu - s^2) $

$ \exp (\mu - v) $

$ \exp (\mu - 1/\tau ) $

Random number

Generate $x_1 \sim \mbox{normal}(0, 1)$, and $\theta = \exp (\mu + sx_1) $ is a draw from the lognormal distribution.


Table 61.26: Negative Binomial Distribution

PROC specification

negbin(n, p)

Density

$ \left( \begin{array}{c} \theta +n-1 \\ n - 1 \end{array} \right) p^ n (1-p)^\theta $

Parameter restriction

$ n = {1, 2, \cdots }, \mbox{and} 0 < p \leq 1 $

Range

$ \theta \in \left\{ \begin{array}{ll} \{ 0, 1, 2, \ldots \} & 0 < p < 1 \\ \{ 0\} & p = 1 \\ \end{array} \right. $

Mean

round$\left(\frac{n(1-p)}{p}\right)$

Variance

$\frac{n(1-p)}{p^2}$

Mode

$ \left\{ \begin{array}{ll} 0 & n = 1 \\ \mbox{round} \left( \frac{(n-1)(1-p)}{p} \right) & n > 1 \end{array} \right. $

Random number

Generate $x_1 \sim \mbox{gamma}(n, 1)$, and $ \theta \sim \mbox{Poisson}(x_1 \cdot (1-p) / p) $ (Fishman, 1996).


Table 61.27: Normal Distribution

PROC specification

normal($\mu $, sd = s)

normal($\mu $, var = v)

normal($\mu $, prec = $\tau $)

Density

$ \frac{1}{s\sqrt {2\pi }} \exp \left( - \frac{(\theta - \mu )^2}{2s^2}\right) $

$ \frac{1}{\sqrt {2\pi v}} \exp \left( - \frac{(\theta - \mu )^2}{2v}\right) $

$ \sqrt {\frac{\tau }{2\pi }} \exp \left( - \frac{\tau (\theta - \mu )^2}{2}\right) $

Parameter restriction

$ s > 0 $

$ v > 0 $

$ \tau > 0 $

Range

$ \theta \in (-\infty , \infty ) $

Same

Same

Mean

$\mu $

Same

Same

Variance

$s^2$

v

$1/\tau $

Mode

$\mu $

Same

Same


Table 61.28: Pareto Distribution

PROC specification

pareto(a, b)

Density

$\frac{a}{b} \left( \frac{b}{\theta } \right)^{a+1} $

Parameter restriction

$ a > 0, b > 0 $

Range

$ \theta \in [b, \infty ) $

Mean

$ \frac{ab}{a-1} $ if $ a > 1 $

Variance

$\frac{b^2a}{(a-1)^2(a-2)}$ if $a > 2$

Mode

b

Random number

Inverse CDF method with $F(\theta ) = 1 - (b/\theta )^ a $ . Generate $u \sim \mbox{uniform}(0,1)$, and $\theta = \frac{b}{u^{1/a}}$ is a draw from the Pareto distribution.

Useful transformation

$x = 1/\theta $ is Beta(a, 1)I{$x < 1/b$}.


Table 61.29: Poisson Distribution

PROC specification

poisson($\lambda $)

Density

$\frac{\lambda ^\theta }{\theta !}\exp (-\lambda )$

Parameter restriction

$ \lambda \geq 0 $

Range

$ \theta \in \left\{ \begin{array}{ll} \{ 0, 1, \ldots \} & \mbox{if} \; \lambda > 0 \\ \{ 0 \} & \mbox{if} \; \lambda = 0 \\ \end{array} \right.$

Mean

$\lambda $

Variance

$\lambda $, if $\lambda > 0 $

Mode

round$(\lambda )$


Table 61.30: Scaled Inverse $\chi ^2$ Distribution

PROC specification

sichisq($\nu , s^2$)

Density

$ \frac{(s^2 \nu /2)^{\nu /2}}{\Gamma (\nu /2)} \theta ^{-(\nu /2+1)} e^{-\nu s^2/(2\theta )} $

Parameter restriction

$ \nu > 0, s > 0 $

Range

$ \theta \in (0, \infty ) $

Mean

$ \frac{\nu }{\nu -2} s^2 $ if $\nu > 2$

Variance

$ \frac{2\nu ^2}{(\nu -2)^2(\nu -4)} s^4 $ if $\nu > 4$

Mode

$ \frac{\nu }{\nu + 2} s^2 $

Random number

Scaled inverse $\chi ^2$ is a special case of the inverse-gamma distribution: $ \theta \sim \mbox{igamma}( \nu /2, \mbox{scale} = (\nu s^2)/2) $ is a draw from the scaled inverse $\chi ^2$ distribution.


Table 61.31: t Distribution

PROC specification

t($\mu $, sd = s, $\nu $)

t($\mu $, var = v, $\nu $)

t($\mu $, prec = $\tau $, $\nu $)

Density

$ \frac{\Gamma ( \frac{\nu +1}{2})}{\Gamma ( \frac{\nu }{2} ) s \sqrt {\nu \pi }} ( 1 + \frac{(\theta -\mu )^2}{\nu s^2}) ^{-\frac{\nu +1}{2}} $

$ \frac{\Gamma ( \frac{\nu +1}{2} )}{\Gamma ( \frac{\nu }{2} ) \sqrt {\nu \pi v}} ( 1 + \frac{ (\theta -\mu )^2 }{\nu v} )^{-\frac{\nu +1}{2}} $

$ \frac{\Gamma ( \frac{\nu +1}{2}) \sqrt {\tau }}{\Gamma ( \frac{\nu }{2} ) \sqrt {\nu \pi }} ( 1 + \frac{\tau (\theta -\mu )^2}{\nu }) ^{-\frac{\nu +1}{2}} $

Parm restriction

$ s > 0 $, $ \nu > 0 $

$ v > 0 $, $ \nu > 0 $

$ \tau > 0 $, $ \nu > 0 $

Range

$ \theta \in (-\infty , \infty ) $

Same

Same

Mean

$ \mu $ if $ \nu > 1 $

Same

Same

Variance

$\frac{\nu }{\nu -2} s^2$ if $ \nu > 2 $

$\frac{\nu }{\nu -2} v$ if $ \nu > 2 $

$\frac{\nu }{\nu -2} \frac{1}{\tau }$ if $ \nu > 2 $

Mode

$ \mu $

Same

Same

Random number

$x_1 \sim \mbox{normal}(0, 1), x_2 \sim \chi ^2(d), \mbox{ and }\theta = m + \sigma x_1 \sqrt {d/x_2}$ is a draw from the t distribution.


Table 61.32: Table (Categorical) Distribution

PROC specification

table($\mb{p}$), where $\mb{p} = \left\{ p_ i \right\} $, for $i = 1, 2, \cdots , k $

Density

$ f(\theta = i) = p_ i$

Parameter restriction

$\sum _ i^ k p_ i = 1$ with all $p_ i > 0$

Range

$ \theta \in \{ 1, 2, \cdots , k \} $

Mode

i such that $p_ i = \mbox{max}(p_1, \cdots , p_ k) $

Random number

Inverse CDF method with $F(\theta = i) = \sum _{j=1}^{i} p_ j$.


Table 61.33: Uniform Distribution

PROC specification

uniform(a, b)

Density

$ \left\{ \begin{array}{ll} \frac{1}{a-b} & \mbox{if} \; a>b \\ \frac{1}{b-a} & \mbox{if} \; b>a \\ 1 & \mbox{if} \; a=b \end{array} \right. $

Parameter restriction

none

Range

$ \theta \in [a, b] $

Mean

$ \frac{a+b}{2} $

Variance

$\frac{|b-a|^2}{12}$

Mode

Does not exist

Random number

Mersenne Twister (Matsumoto and Kurita, 1992, 1994; Matsumoto and Nishimura, 1998)


Table 61.34: Wald Distribution

PROC specification

wald($\mu $, $\lambda $)

Density

$\sqrt {\frac{\lambda }{2\pi \theta ^3}} \exp \left( \frac{-\lambda (\theta -\mu )^2}{2\mu ^2\theta }\right) $

Parameter restriction

$ \mu > 0, \lambda > 0 $

Range

$ \theta \in (0, \infty ) $

Mean

$ \mu $

Variance

$ \mu ^3 / \lambda $

Mode

$ \mu \left[ \left( 1 + \frac{9\mu ^2}{4\lambda ^2}\right)^{1/2} - \frac{3\mu }{2\lambda } \right]$

Random number

Generate $\nu _0 \sim \chi ^2_{(1)}$. Let $x_1 = \mu + \frac{\mu ^2 \nu _0}{2\lambda } - \frac{\mu }{2\lambda } \sqrt {4\mu \lambda \nu _0 + \mu ^2\nu _0^2}$ and $x_2 = \mu ^2/x_1 $. Perform a Bernoulli trial, $ w \sim \mbox{Bernoulli}(\frac{\mu }{\mu + x_1})$. If $w = 1$, choose $\theta = x_1$; otherwise, choose $\theta = x_2$ (Michael, Schucany, and Haas, 1976).


Table 61.35: Weibull Distribution

PROC specification

weibull($\mu $, c, $\sigma $)

Density

$ \exp \left( - \left( \frac{\theta - \mu }{\sigma } \right)^ c \right) \frac{c}{\sigma } \left( \frac{\theta - \mu }{\sigma } \right)^{c-1} $

Parameter restriction

$ c > 0, \sigma > 0 $

Range

$ \theta \in [\mu , \infty ) $ if $c=1; (\mu , \infty ) $ otherwise

Mean

$\mu + \sigma \Gamma (1 + 1/c) $

Variance

$\sigma ^2 [\Gamma (1+2/c) - \Gamma ^2(1+1/c)]$

Mode

$\mu + \sigma (1 - 1/c)^{1/c} $ if $c > 1$

Random number

Inverse CDF method with $F(\theta ) = 1 - \exp \left(-\left(- \frac{\theta - \mu }{\sigma } \right)^{c} \right) $. Generate $u \sim \mbox{uniform}(0, 1)$, and $\theta = \mu + \sigma \cdot (- \ln u)^{1/c}$ is a draw from the Weibull distribution.


Multivariate Distributions

Table 61.36: Dirichlet Distribution

PROC specification

$\bm {\theta } \sim $ dirich($\bm {\alpha }$), where $\bm {\theta } = \left\{ \theta _ i \right\} , \bm {\alpha } = \left\{ \alpha _ i \right\} $, for $i = 1, 2, \cdots , k$

Density

$\frac{\Gamma (\alpha _0)}{\prod _{i=1}^ k\Gamma (\alpha _ i)} \prod _{i=1}^{k} \theta _ i^{\alpha _ i-1}$, where $\alpha _0 = \sum _{i=1}^{k} \alpha _ i$

Parameter restriction

$\alpha _ i > 0$

Range

$\theta _ i > 0$, $\sum _{i=1}^ k \theta _ i = 1$

Mean

$\alpha _ j \left/ \alpha _0 \right.$

Mode

$\left( \alpha _ j - 1\right) \left/ \left(\alpha _0 - k \right) \right.$


Table 61.37: Inverse Wishart Distribution

PROC specification

$\bm {\theta } \sim $ iwishart($\nu $, $\mb{S}$), both $\bm {\theta }$ and $\mb{S}$ are $k \times k$ matrices

Density

$\left( 2^{\frac{\nu k}{2}} \pi ^{\frac{k(k-1)}{4}} \prod _{i=1}^ k \Gamma \left( \frac{\nu +1-i}{2}\right) \right)^{-1} |\mb{S}|^{\frac{\nu }{2}}|\bm {\theta }|^{-\frac{\nu +k+1}{2}} \exp \left(-\frac{1}{2} \mr{tr} (\mb{S}\bm {\theta }^{-1}) \right) $

Parameter restriction

$\mb{S}$ must be symmetric and positive definite; $\nu > k - 1$

Range

$\bm {\theta }$ is symmetric and positive definite

Mean

$\mb{S} \left/ \left(\nu - k - 1\right) \right.$

Mode

$\mb{S} \left/ \left(\nu + k + 1\right) \right.$


Table 61.38: Multivariate Normal Distribution

PROC specification

$\bm {\theta } \sim $ mvn($\bm {\mu }$, $\bSigma $), where $\bm {\theta } = \left\{ \theta _ k \right\} , \bm {\mu } = \left\{ \mu _ k \right\} $, for $i=1, 2, \cdots , k$, and $\bSigma $ is a $k \times k$ variance matrix

Density

$\exp \left(-\frac{1}{2} (\bm {\theta }-\bm {\mu })’ \bSigma ^{-1} (\bm {\theta }-\bm {\mu }) \right) \left/ {\sqrt {(2\pi )^ k \left| \bSigma \right|}} \right.$

Parameter restriction

$\bSigma $ must be symmetric and positive definite

Range

$-\infty < \theta _ i < \infty $

Mean

$\bm {\mu }$

Mode

$\bm {\mu }$


Table 61.39: Autoregressive Multivariate Normal Distribution

PROC specification

$\bm {\theta }\sim $mvnar($\bm {\mu }$, sd=$\sigma $,$\rho $)

$\bm {\theta }\sim $mvnar($\bm {\mu }$, var=$\sigma ^2$,$\rho $)

$\bm {\theta }\sim $mvnar($\bm {\mu }$, prec=$1/\sigma ^2$, $\rho $)

Density

$\exp \left(-\frac{1}{2} (\bm {\theta }-\bm {\mu })’ (\sigma ^2 \bSigma ) ^{-1}(\bm {\theta }-\bm {\mu }) \right) \left/ {\sqrt {(2\pi )^ k \left| (\sigma ^2 \bSigma ) \right|}} \right.$ where

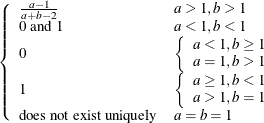
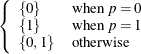
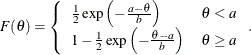
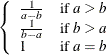
\[ \bSigma = \left[ \begin{array}{cccccc} 1 & \rho & \rho ^2 & \rho ^3 & \cdots & \rho ^ k \\ \rho & 1 & \rho & \rho ^2 & \cdots & \rho ^{k-1} \\ \rho ^2 & \rho & 1 & \rho & \cdots & \rho ^{k-2} \\ \rho ^3 & \rho ^2 & \rho & 1 & \cdots & \rho ^{k-3} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \rho ^ k & \rho ^{k-1} & \rho ^{k-2} & \rho ^{k-3} & \cdots & 1 \\ \end{array} \right] \]

Parameter restriction

$\sigma > 0$ and $-1 < \rho < 1$

Range

$-\infty < \theta _ i < \infty $

Mean

$\bm {\mu }$

Mode

$\bm {\mu }$

Special Case

When $\rho = 0$, the distribution simplifies to mvn($\bm {\mu }$, $\sigma ^2 \cdot \mb{I}_ k$), where $\mb{I}_ k$ denotes the $k \times k$ identity matrix


Table 61.40: Multinomial Distribution

PROC specification

$\bm {\theta } \sim $ multinom($\mb{p}$), where $\bm {\theta } = \left\{ \theta _ i \right\} $ and $\mb{p} = \left\{ p_ i \right\} $, for $i = 1, 2, \cdots , k$

Density

$\frac{n!}{\theta _1 \cdots \theta _ k} p_1^{\theta _1} \cdots p_ k^{\theta _ k}$, where $\sum _ i^ k \theta _ i = n$

Parameter restriction

$\sum _ i^ k p_ i = 1$ with all $p_ i > 0$

Range

$\theta _ i \in \left\{ 0, \cdots , n \right\} $, nonnegative integers

Mean

$n \cdot \mb{p}$