The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data - References
Researchers investigated the performance of two medical procedures in a multicenter study. They randomly selected 15 centers
for inclusion. One of the study goals was to compare the occurrence of side effects for the procedures. In each center ![]() patients were randomly selected and assigned to procedure “A,” and
patients were randomly selected and assigned to procedure “A,” and ![]() patients were randomly assigned to procedure “B.” The following DATA step creates the data set for the analysis:
patients were randomly assigned to procedure “B.” The following DATA step creates the data set for the analysis:
data multicenter; input center group$ n sideeffect; datalines; 1 A 32 14 1 B 33 18 2 A 30 4 2 B 28 8 3 A 23 14 3 B 24 9 4 A 22 7 4 B 22 10 5 A 20 6 5 B 21 12 6 A 19 1 6 B 20 3 7 A 17 2 7 B 17 6 8 A 16 7 8 B 15 9 9 A 13 1 9 B 14 5 10 A 13 3 10 B 13 1 11 A 11 1 11 B 12 2 12 A 10 1 12 B 9 0 13 A 9 2 13 B 9 6 14 A 8 1 14 B 8 1 15 A 7 1 15 B 8 0 ;
The variable group identifies the two procedures, n is the number of patients who received a given procedure in a particular center, and sideeffect is the number of patients who reported side effects.
If ![]() and
and ![]() denote the number of patients in center i who report side effects for procedures A and B, respectively, then—for a given center—these are independent binomial random variables. To model the probability of side
effects for the two drugs,
denote the number of patients in center i who report side effects for procedures A and B, respectively, then—for a given center—these are independent binomial random variables. To model the probability of side
effects for the two drugs, ![]() and
and ![]() , you need to account for the fixed group effect and the random selection of centers. One possibility is to assume a model
that relates group and center effects linearly to the logit of the probabilities:
, you need to account for the fixed group effect and the random selection of centers. One possibility is to assume a model
that relates group and center effects linearly to the logit of the probabilities:
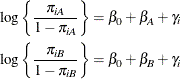
In this model, ![]() measures the difference in the logits of experiencing side effects, and the
measures the difference in the logits of experiencing side effects, and the ![]() are independent random variables due to the random selection of centers. If you think of
are independent random variables due to the random selection of centers. If you think of ![]() as the overall intercept in the model, then the
as the overall intercept in the model, then the ![]() are random intercept adjustments. Observations from the same center receive the same adjustment, and these vary randomly
from center to center with variance
are random intercept adjustments. Observations from the same center receive the same adjustment, and these vary randomly
from center to center with variance ![]() .
.
Because ![]() is the conditional mean of the sample proportion,
is the conditional mean of the sample proportion, ![]() , you can model the sample proportions as binomial ratios in a generalized linear mixed model. The following statements request
this analysis under the assumption of normally distributed center effects with equal variance and a logit link function:
, you can model the sample proportions as binomial ratios in a generalized linear mixed model. The following statements request
this analysis under the assumption of normally distributed center effects with equal variance and a logit link function:
proc glimmix data=multicenter; class center group; model sideeffect/n = group / solution; random intercept / subject=center; run;
The PROC GLIMMIX statement invokes the procedure. The CLASS statement instructs the procedure to treat the variables center and group as classification variables. The MODEL statement specifies the response variable as a sample proportion by using the events/trials syntax. In terms of the previous formulas, sideeffect/n corresponds to ![]() for observations from group A and to
for observations from group A and to ![]() for observations from group B. The SOLUTION option in the MODEL statement requests a listing of the solutions for the fixed-effects parameter estimates. Note that because of the events/trials syntax, the GLIMMIX procedure defaults to the binomial distribution, and that distribution’s default link is the logit link.
The RANDOM statement specifies that the linear predictor contains an intercept term that randomly varies at the level of the
for observations from group B. The SOLUTION option in the MODEL statement requests a listing of the solutions for the fixed-effects parameter estimates. Note that because of the events/trials syntax, the GLIMMIX procedure defaults to the binomial distribution, and that distribution’s default link is the logit link.
The RANDOM statement specifies that the linear predictor contains an intercept term that randomly varies at the level of the center effect. In other words, a random intercept is drawn separately and independently for each center in the study.
The results of this analysis are shown in Figure 43.1–Figure 43.9.
The “Model Information Table” in Figure 43.1 summarizes important information about the model you fit and about aspects of the estimation technique.
Figure 43.1: Model Information
| Model Information | |
|---|---|
| Data Set | WORK.MULTICENTER |
| Response Variable (Events) | sideeffect |
| Response Variable (Trials) | n |
| Response Distribution | Binomial |
| Link Function | Logit |
| Variance Function | Default |
| Variance Matrix Blocked By | center |
| Estimation Technique | Residual PL |
| Degrees of Freedom Method | Containment |
PROC GLIMMIX recognizes the variables sideeffect and n as the numerator and denominator in the events/trials syntax, respectively. The distribution—conditional on the random center effects—is binomial. The marginal variance matrix
is block-diagonal, and observations from the same center form the blocks. The default estimation technique in generalized
linear mixed models is residual pseudo-likelihood with a subject-specific expansion (METHOD=RSPL).
The “Class Level Information” table lists the levels of the variables specified in the CLASS statement and the ordering of the levels. The “Number of Observations” table displays the number of observations read and used in the analysis (Figure 43.2).
Figure 43.2: Class Level Information and Number of Observations
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| center | 15 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
| group | 2 | A B |
| Number of Observations Read | 30 |
|---|---|
| Number of Observations Used | 30 |
| Number of Events | 155 |
| Number of Trials | 503 |
There are two variables listed in the CLASS statement. The center variable has fifteen levels, and the group variable has two levels. Because the response is specified through the events/trial syntax, the “Number of Observations” table also contains the total number of events and trials used in the analysis.
The “Dimensions” table lists the size of relevant matrices (Figure 43.3).
Figure 43.3: Dimensions
| Dimensions | |
|---|---|
| G-side Cov. Parameters | 1 |
| Columns in X | 3 |
| Columns in Z per Subject | 1 |
| Subjects (Blocks in V) | 15 |
| Max Obs per Subject | 2 |
There are three columns in the ![]() matrix, corresponding to an intercept and the two levels of the
matrix, corresponding to an intercept and the two levels of the group variable. For each subject (center), the ![]() matrix contains only an intercept column.
matrix contains only an intercept column.
The “Optimization Information” table provides information about the methods and size of the optimization problem (Figure 43.4).
Figure 43.4: Optimization Information
| Optimization Information | |
|---|---|
| Optimization Technique | Dual Quasi-Newton |
| Parameters in Optimization | 1 |
| Lower Boundaries | 1 |
| Upper Boundaries | 0 |
| Fixed Effects | Profiled |
| Starting From | Data |
The default optimization technique for generalized linear mixed models with binomial data is the quasi-Newton method. Because
a residual likelihood technique is used to compute the objective function, only the
covariance parameters participate in the optimization. A lower boundary constraint is placed on the variance component for
the random center effect. The solution for this variance cannot be less than zero.
The “Iteration History” table displays information about the progress of the optimization process. After the initial optimization, the GLIMMIX procedure performed 15 updates before the convergence criterion was met (Figure 43.5). At convergence, the largest absolute value of the gradient was near zero. This indicates that the process stopped at an extremum of the objective function.
Figure 43.5: Iteration History and Convergence Status
| Iteration History | |||||
|---|---|---|---|---|---|
| Iteration | Restarts | Subiterations | Objective Function |
Change | Max Gradient |
| 0 | 0 | 5 | 79.688580269 | 0.11807224 | 7.851E-7 |
| 1 | 0 | 3 | 81.294622554 | 0.02558021 | 8.209E-7 |
| 2 | 0 | 2 | 81.438701534 | 0.00166079 | 4.061E-8 |
| 3 | 0 | 1 | 81.444083567 | 0.00006263 | 2.311E-8 |
| 4 | 0 | 1 | 81.444265216 | 0.00000421 | 0.000025 |
| 5 | 0 | 1 | 81.444277364 | 0.00000383 | 0.000023 |
| 6 | 0 | 1 | 81.444266322 | 0.00000348 | 0.000021 |
| 7 | 0 | 1 | 81.44427636 | 0.00000316 | 0.000019 |
| 8 | 0 | 1 | 81.444267235 | 0.00000287 | 0.000017 |
| 9 | 0 | 1 | 81.444275529 | 0.00000261 | 0.000016 |
| 10 | 0 | 1 | 81.44426799 | 0.00000237 | 0.000014 |
| 11 | 0 | 1 | 81.444274843 | 0.00000216 | 0.000013 |
| 12 | 0 | 1 | 81.444268614 | 0.00000196 | 0.000012 |
| 13 | 0 | 1 | 81.444274277 | 0.00000178 | 0.000011 |
| 14 | 0 | 1 | 81.444269129 | 0.00000162 | 9.772E-6 |
| 15 | 0 | 0 | 81.444273808 | 0.00000000 | 9.102E-6 |
| Convergence criterion (PCONV=1.11022E-8) satisfied. |
The “Fit Statistics” table lists information about the fitted model (Figure 43.6).
Figure 43.6: Fit Statistics
| Fit Statistics | |
|---|---|
| -2 Res Log Pseudo-Likelihood | 81.44 |
| Generalized Chi-Square | 30.69 |
| Gener. Chi-Square / DF | 1.10 |
Twice the negative of the residual log likelihood in the final pseudo-model equaled 81.44. The ratio of the generalized chi-square statistic and its degrees of freedom is close to 1. This is a measure of the residual variability in the marginal distribution of the data.
The “Covariance Parameter Estimates” table displays estimates and asymptotic estimated standard errors for all covariance parameters (Figure 43.7).
Figure 43.7: Covariance Parameter Estimates
| Covariance Parameter Estimates | |||
|---|---|---|---|
| Cov Parm | Subject | Estimate | Standard Error |
| Intercept | center | 0.6176 | 0.3181 |
The variance of the random center intercepts on the logit scale is estimated as ![]() .
.
The “Parameter Estimates” table displays the solutions for the fixed effects in the model (Figure 43.8).
Figure 43.8: Parameter Estimates
| Solutions for Fixed Effects | ||||||
|---|---|---|---|---|---|---|
| Effect | group | Estimate | Standard Error | DF | t Value | Pr > |t| |
| Intercept | -0.8071 | 0.2514 | 14 | -3.21 | 0.0063 | |
| group | A | -0.4896 | 0.2034 | 14 | -2.41 | 0.0305 |
| group | B | 0 | . | . | . | . |
Because of the fixed-effects parameterization used in the GLIMMIX procedure, the “Intercept” effect is an estimate of ![]() , and the “A” group effect is an estimate of
, and the “A” group effect is an estimate of ![]() , the log odds ratio. The associated estimated probabilities of side effects in the two groups are
, the log odds ratio. The associated estimated probabilities of side effects in the two groups are
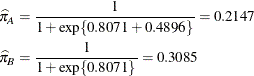
There is a significant difference between the two groups (p = 0.0305).
The “Type III Tests of Fixed Effect” table displays significance tests for the fixed effects in the model (Figure 43.9).
Figure 43.9: Type III Tests of Fixed Effects
| Type III Tests of Fixed Effects | ||||
|---|---|---|---|---|
| Effect | Num DF | Den DF | F Value | Pr > F |
| group | 1 | 14 | 5.79 | 0.0305 |
Because the group effect has only two levels, the p-value for the effect is the same as in the “Parameter Estimates” table, and the “F Value” is the square of the “t Value” shown there.
You can produce the estimates of the average logits in the two groups and their predictions on the scale of the data with the LSMEANS statement in PROC GLIMMIX:
ods select lsmeans; proc glimmix data=multicenter; class center group; model sideeffect/n = group / solution; random intercept / subject=center; lsmeans group / cl ilink; run;
The LSMEANS statement requests the least squares means of the group effect on the logit scale. The CL option requests their
confidence limits. The ILINK option adds estimates, standard errors, and confidence limits on the mean (probability) scale (Figure 43.10).
Figure 43.10: Least Squares Means
| group Least Squares Means | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| group | Estimate | Standard Error | DF | t Value | Pr > |t| | Alpha | Lower | Upper | Mean | Standard Error Mean |
Lower Mean |
Upper Mean |
| A | -1.2966 | 0.2601 | 14 | -4.99 | 0.0002 | 0.05 | -1.8544 | -0.7388 | 0.2147 | 0.04385 | 0.1354 | 0.3233 |
| B | -0.8071 | 0.2514 | 14 | -3.21 | 0.0063 | 0.05 | -1.3462 | -0.2679 | 0.3085 | 0.05363 | 0.2065 | 0.4334 |
The “Estimate” column displays the least squares mean estimate on the logit scale, and the “Mean” column represents its mapping onto the probability scale. The “Lower” and “Upper” columns are 95% confidence limits for the logits in the two groups. The “Lower Mean” and “Upper Mean” columns are the corresponding confidence limits for the probabilities of side effects. These limits are obtained by inversely linking the confidence bounds on the linear scale, and thus are not symmetric about the estimate of the probabilities.