The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data - References
A generalized linear model consists of the following:
-
a linear predictor
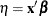
-
a monotonic mapping between the mean of the data and the linear predictor
-
a response distribution in the exponential family of distributions
A density or mass function in this family can be written as
for some functions ![]() and
and ![]() . The parameter
. The parameter ![]() is called the natural (canonical) parameter. The parameter
is called the natural (canonical) parameter. The parameter ![]() is a
scale parameter, and it is not present in all exponential family distributions. See Table 43.20 for a list of distributions for which
is a
scale parameter, and it is not present in all exponential family distributions. See Table 43.20 for a list of distributions for which ![]() . In the case where observations are weighted, the scale parameter is replaced with
. In the case where observations are weighted, the scale parameter is replaced with ![]() in the preceding density (or mass function), where w is the weight associated with the observation y.
in the preceding density (or mass function), where w is the weight associated with the observation y.
The mean and variance of the data are related to the components of the density, ![]() ,
, ![]() , where primes denote first and second derivatives. If you express
, where primes denote first and second derivatives. If you express ![]() as a function of
as a function of ![]() , the relationship is known as the natural link or the canonical link function. In other words, modeling data with a canonical
link assumes that
, the relationship is known as the natural link or the canonical link function. In other words, modeling data with a canonical
link assumes that ![]() ; the effect contributions are additive on the canonical scale. The second derivative of
; the effect contributions are additive on the canonical scale. The second derivative of ![]() , expressed as a function of
, expressed as a function of ![]() , is the variance function of the generalized linear model,
, is the variance function of the generalized linear model, ![]() . Note that because of this relationship, the distribution determines the variance function and the canonical link function.
You cannot, however, proceed in the opposite direction. If you provide a user-specified variance function, the GLIMMIX procedure
assumes that only the first two moments of the response distribution are known. The full distribution of the data is then
unknown and maximum likelihood estimation is not possible. Instead, the GLIMMIX procedure then estimates parameters by quasi-likelihood.
. Note that because of this relationship, the distribution determines the variance function and the canonical link function.
You cannot, however, proceed in the opposite direction. If you provide a user-specified variance function, the GLIMMIX procedure
assumes that only the first two moments of the response distribution are known. The full distribution of the data is then
unknown and maximum likelihood estimation is not possible. Instead, the GLIMMIX procedure then estimates parameters by quasi-likelihood.