The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data - References
If you use an empirical (sandwich) estimator with the EMPIRICAL= option in the PROC GLIMMIX statement, the procedure replaces the model-based estimator of the covariance of the fixed effects with the sandwich estimator. This affects aspects of inference, such as prediction standard errors, tests of fixed effects, estimates, contrasts, and so forth. Similarly, if you choose the DDFM=KENWARDROGER degrees-of-freedom method in the MODEL statement, PROC GLIMMIX adjusts the model-based covariance matrix of the fixed effects according to Kenward and Roger (1997) or according to Kackar and Harville (1984) and Harville and Jeske (1992).
In this situation, the COVB(DETAILS) option in the MODEL statement has two effects. The GLIMMIX procedure displays the (adjusted) covariance matrix of the fixed effects and the model-based covariance matrix (the ODS name of the table with the model-based covariance matrix is CovBModelBased). The procedure also displays a table of statistics for the unadjusted and adjusted covariance matrix and for their comparison. The ODS name of this table is CovBDetails.
If the model-based covariance matrix is not replaced with an adjusted estimator, the COVB(DETAILS) option displays the model-based covariance matrix and provides diagnostic measures for it in the CovBDetails table.
The table generated by the COVB(DETAILS) option consists of several sections. See Example 43.8 for an application.
The trace and log determinant of covariance matrices are general scalar summaries that are sometimes used in direct comparisons, or in formulating other statistics, such as the difference of log determinants. The trace simply represents the sum of the variances of all fixed-effects parameters. If a matrix is indefinite, the determinant is reported instead of the log determinant.
The model-based and adjusted covariance matrices should have the same general makeup of eigenvalues. There should not be any negative eigenvalues, and they should have the same numbers of positive and zero eigenvalues. A reduction in rank due to the adjustment is troublesome for aspects of inference. Negative eigenvalues are listed in the table only if they occur, because a covariance matrix should be at least positive semi-definite. However, the GLIMMIX procedure examines the model-based and adjusted covariance matrix for negative eigenvalues. The condition numbers reported by PROC GLIMMIX for positive (semi-)definite matrices are computed as the ratio of the largest and smallest nonzero eigenvalue. A large condition number reflects poor conditioning of the matrix.
Matrix norms are extensions of the concept of vector norms to measure the “length” of a matrix. The Frobenius norm of an ![]() matrix
matrix ![]() is the direct equivalent of the Euclidean vector norm, the square root of the sum of the squared elements,
is the direct equivalent of the Euclidean vector norm, the square root of the sum of the squared elements,
![\[ ||\mb {A}||_ F = \sqrt { \sum _{i=1}^{n} \, \sum _{j=1}^{n} a_{ij}^2 } \]](images/statug_glimmix0829.png)
The ![]() - and 1-norms of matrix
- and 1-norms of matrix ![]() are the maximum absolute row and column sums, respectively:
are the maximum absolute row and column sums, respectively:
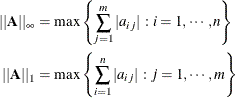
These two norms are identical for symmetric matrices.
The “Comparison” section of the CovBDetails table provides several statistics that set the matrices in relationship. The concordance correlation
reported by the GLIMMIX procedure is a standardized measure of the closeness of the model-based and adjusted covariance matrix.
It is a slight modification of the covariance concordance correlation in Vonesh, Chinchilli, and Pu (1996) and Vonesh and Chinchilli (1997, Ch. 8.3). Denote as ![]() the
the ![]() model-based covariance matrix and as
model-based covariance matrix and as ![]() the adjusted matrix. Suppose that
the adjusted matrix. Suppose that ![]() is the matrix obtained from the identity matrix of size p by replacing diagonal elements corresponding to singular rows in
is the matrix obtained from the identity matrix of size p by replacing diagonal elements corresponding to singular rows in ![]() with zeros. The lower triangular portion of
with zeros. The lower triangular portion of ![]() is stored in vector
is stored in vector ![]() and the lower triangular portion of
and the lower triangular portion of ![]() is stored in vector
is stored in vector ![]() . The matrix
. The matrix ![]() is constructed from an eigenanalysis of
is constructed from an eigenanalysis of ![]() and is symmetric. The covariance concordance correlation is then
and is symmetric. The covariance concordance correlation is then
This measure is 1 if ![]() =
= ![]() . If
. If ![]() is orthogonal to
is orthogonal to ![]() , there is total disagreement between the model-based and the adjusted covariance matrix and
, there is total disagreement between the model-based and the adjusted covariance matrix and ![]() is zero.
is zero.
The discrepancy function reported by PROC GLIMMIX is computed as
In diagnosing departures between an assumed covariance structure and ![]() —using an empirical estimator—Vonesh, Chinchilli, and Pu (1996) find that the concordance correlation is useful in detecting gross departures and propose
—using an empirical estimator—Vonesh, Chinchilli, and Pu (1996) find that the concordance correlation is useful in detecting gross departures and propose ![]() to test the correctness of the assumed model, where
to test the correctness of the assumed model, where ![]() denotes the number of subjects.
denotes the number of subjects.