The REG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing Values Input Data Sets Output Data Sets Interactive Analysis Model-Selection Methods Criteria Used in Model-Selection Methods Limitations in Model-Selection Methods Parameter Estimates and Associated Statistics Predicted and Residual Values Models of Less Than Full Rank Collinearity Diagnostics Model Fit and Diagnostic Statistics Influence Statistics Reweighting Observations in an Analysis Testing for Heteroscedasticity Testing for Lack of Fit Multivariate Tests Autocorrelation in Time Series Data Computations for Ridge Regression and IPC Analysis Construction of Q-Q and P-P Plots Computational Methods Computer Resources in Regression Analysis Displayed Output ODS Table Names ODS Graphics
Missing Values Input Data Sets Output Data Sets Interactive Analysis Model-Selection Methods Criteria Used in Model-Selection Methods Limitations in Model-Selection Methods Parameter Estimates and Associated Statistics Predicted and Residual Values Models of Less Than Full Rank Collinearity Diagnostics Model Fit and Diagnostic Statistics Influence Statistics Reweighting Observations in an Analysis Testing for Heteroscedasticity Testing for Lack of Fit Multivariate Tests Autocorrelation in Time Series Data Computations for Ridge Regression and IPC Analysis Construction of Q-Q and P-P Plots Computational Methods Computer Resources in Regression Analysis Displayed Output ODS Table Names ODS Graphics -
Examples

- References
Example 76.4 Regression with Quantitative and Qualitative Variables
At times it is desirable to have independent variables in the model that are qualitative rather than quantitative. This is easily handled in a regression framework. Regression uses qualitative variables to distinguish between populations. There are two main advantages of fitting both populations in one model. You gain the ability to test for different slopes or intercepts in the populations, and more degrees of freedom are available for the analysis.
Regression with qualitative variables is different from analysis of variance and analysis of covariance. Analysis of variance uses qualitative independent variables only. Analysis of covariance uses quantitative variables in addition to the qualitative variables in order to account for correlation in the data and reduce MSE; however, the quantitative variables are not of primary interest and merely improve the precision of the analysis.
Consider the case where 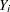 is the dependent variable,
is the dependent variable, 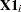 is a quantitative variable,
is a quantitative variable, 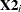 is a qualitative variable taking on values 0 or 1, and
is a qualitative variable taking on values 0 or 1, and 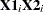 is the interaction. The variable
is the interaction. The variable 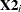 is called a dummy, binary, or indicator variable. With values 0 or 1, it distinguishes between two populations. The model is of the form
is called a dummy, binary, or indicator variable. With values 0 or 1, it distinguishes between two populations. The model is of the form
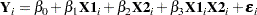 |
for the observations 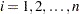 . The parameters to be estimated are
. The parameters to be estimated are 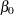 ,
, 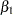 ,
,  , and
, and 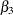 . The number of dummy variables used is one less than the number of qualitative levels. This yields a nonsingular
. The number of dummy variables used is one less than the number of qualitative levels. This yields a nonsingular 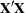 matrix. See Chapter 10 of Neter, Wasserman, and Kutner (1990) for more details.
matrix. See Chapter 10 of Neter, Wasserman, and Kutner (1990) for more details.
An example from Neter, Wasserman, and Kutner (1990) follows. An economist is investigating the relationship between the size of an insurance firm and the speed at which it implements new insurance innovations. He believes that the type of firm might affect this relationship and suspects that there might be some interaction between the size and type of firm. The dummy variable in the model enables the two firms to have different intercepts. The interaction term enables the firms to have different slopes as well.
In this study, 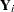 is the number of months from the time the first firm implemented the innovation to the time it was implemented by the
is the number of months from the time the first firm implemented the innovation to the time it was implemented by the 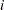 th firm. The variable
th firm. The variable 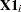 is the size of the firm, measured in total assets of the firm. The variable
is the size of the firm, measured in total assets of the firm. The variable 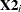 denotes the firm type; it is 0 if the firm is a mutual fund company and 1 if the firm is a stock company. The dummy variable enables each firm type to have a different intercept and slope.
denotes the firm type; it is 0 if the firm is a mutual fund company and 1 if the firm is a stock company. The dummy variable enables each firm type to have a different intercept and slope.
The previous model can be broken down into a model for each firm type by plugging in the values for 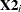 . If
. If 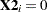 , the model is
, the model is
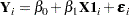 |
This is the model for a mutual company. If 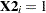 , the model for a stock firm is
, the model for a stock firm is
 |
This model has intercept 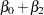 and slope
and slope 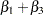 .
.
The data1 follow. Note that the interaction term is created in the DATA step since polynomial effects such as size*type are not allowed in the MODEL statement in the REG procedure.
title 'Regression With Quantitative and Qualitative Variables'; data insurance; input time size type @@; sizetype=size*type; datalines; 17 151 0 26 92 0 21 175 0 30 31 0 22 104 0 0 277 0 12 210 0 19 120 0 4 290 0 16 238 0 28 164 1 15 272 1 11 295 1 38 68 1 31 85 1 21 224 1 20 166 1 13 305 1 30 124 1 14 246 1 ; run;
The following statements begin the analysis:
proc reg data=insurance; model time = size type sizetype; run;
The ANOVA table is displayed in Output 76.4.1.
| Regression With Quantitative and Qualitative Variables |
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 3 | 1504.41904 | 501.47301 | 45.49 | <.0001 |
| Error | 16 | 176.38096 | 11.02381 | ||
| Corrected Total | 19 | 1680.80000 | |||
| Root MSE | 3.32021 | R-Square | 0.8951 |
|---|---|---|---|
| Dependent Mean | 19.40000 | Adj R-Sq | 0.8754 |
| Coeff Var | 17.11450 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | 33.83837 | 2.44065 | 13.86 | <.0001 |
| size | 1 | -0.10153 | 0.01305 | -7.78 | <.0001 |
| type | 1 | 8.13125 | 3.65405 | 2.23 | 0.0408 |
| sizetype | 1 | -0.00041714 | 0.01833 | -0.02 | 0.9821 |
The overall 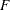 statistic is significant (
statistic is significant (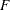 =45.490,
=45.490, 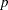 <0.0001). The interaction term is not significant (
<0.0001). The interaction term is not significant ( =
= 0.023,
0.023, 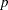 =0.9821). Hence, this term should be removed and the model refitted, as shown in the following statements:
=0.9821). Hence, this term should be removed and the model refitted, as shown in the following statements:
delete sizetype; print; run;
The DELETE statement removes the interaction term (sizetype) from the model. The new ANOVA and parameter estimates tables are shown in Output 76.4.2.
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 2 | 1504.41333 | 752.20667 | 72.50 | <.0001 |
| Error | 17 | 176.38667 | 10.37569 | ||
| Corrected Total | 19 | 1680.80000 | |||
| Root MSE | 3.22113 | R-Square | 0.8951 |
|---|---|---|---|
| Dependent Mean | 19.40000 | Adj R-Sq | 0.8827 |
| Coeff Var | 16.60377 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | 33.87407 | 1.81386 | 18.68 | <.0001 |
| size | 1 | -0.10174 | 0.00889 | -11.44 | <.0001 |
| type | 1 | 8.05547 | 1.45911 | 5.52 | <.0001 |
The overall 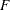 statistic is still significant (
statistic is still significant (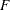 =72.497,
=72.497, 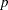 <0.0001). The intercept and the coefficients associated with size and type are significantly different from zero (
<0.0001). The intercept and the coefficients associated with size and type are significantly different from zero ( =18.675,
=18.675, 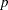 <0.0001;
<0.0001;  =
= 11.443,
11.443, 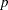 <0.0001;
<0.0001;  =5.521,
=5.521, 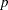 <0.0001, respectively). Notice that the
<0.0001, respectively). Notice that the 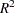 did not change with the omission of the interaction term.
did not change with the omission of the interaction term.
The fitted model is
 |
The fitted model for a mutual fund company (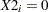 ) is
) is
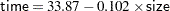 |
and the fitted model for a stock company (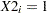 ) is
) is
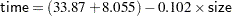 |
So the two models have different intercepts but the same slope.
The following statements first use an OUTPUT statement to save the residuals and predicted values from the new model in the OUT= data set. Next PROC SGPLOT is used to produce Output 76.4.3, which plots residuals versus predicted values. The firm type is used as the plot symbol; this can be useful in determining if the firm types have different residual patterns.
output out=out r=r p=p; run; proc sgplot data=out; scatter x=p y=r / markerchar=type group=type; run;
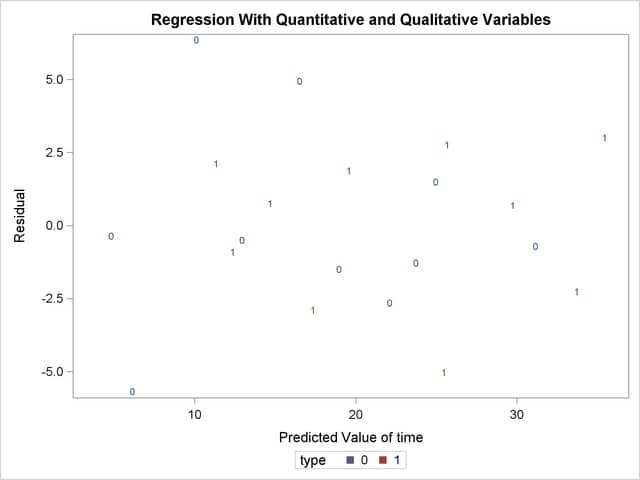
The residuals show no major trend. Neither firm type by itself shows a trend either. This indicates that the model is satisfactory.
The following statements produce the plot of the predicted values versus size that appears in Output 76.4.4, where the firm type is again used as the plotting symbol:
proc sgplot data=out; scatter x=size y=p / markerchar=type group=type; run;
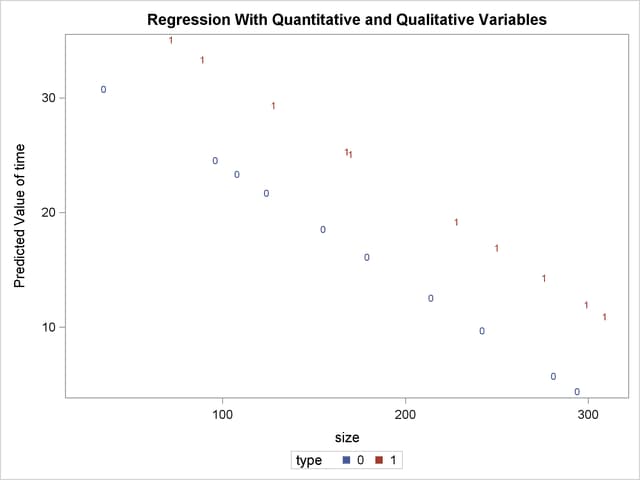
The different intercepts are very evident in this plot.