The REG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing Values Input Data Sets Output Data Sets Interactive Analysis Model-Selection Methods Criteria Used in Model-Selection Methods Limitations in Model-Selection Methods Parameter Estimates and Associated Statistics Predicted and Residual Values Models of Less Than Full Rank Collinearity Diagnostics Model Fit and Diagnostic Statistics Influence Statistics Reweighting Observations in an Analysis Testing for Heteroscedasticity Testing for Lack of Fit Multivariate Tests Autocorrelation in Time Series Data Computations for Ridge Regression and IPC Analysis Construction of Q-Q and P-P Plots Computational Methods Computer Resources in Regression Analysis Displayed Output ODS Table Names ODS Graphics
Missing Values Input Data Sets Output Data Sets Interactive Analysis Model-Selection Methods Criteria Used in Model-Selection Methods Limitations in Model-Selection Methods Parameter Estimates and Associated Statistics Predicted and Residual Values Models of Less Than Full Rank Collinearity Diagnostics Model Fit and Diagnostic Statistics Influence Statistics Reweighting Observations in an Analysis Testing for Heteroscedasticity Testing for Lack of Fit Multivariate Tests Autocorrelation in Time Series Data Computations for Ridge Regression and IPC Analysis Construction of Q-Q and P-P Plots Computational Methods Computer Resources in Regression Analysis Displayed Output ODS Table Names ODS Graphics -
Examples

- References
Example 76.3 Predicting Weight by Height and Age
In this example, the weights of schoolchildren are modeled as a function of their heights and ages. The example shows the use of a BY statement with PROC REG, multiple MODEL statements, and the OUTEST= and OUTSSCP= options, which create data sets. Here are the data:
*------------Data on Age, Weight, and Height of Children-------* | Age (months), height (inches), and weight (pounds) were | | recorded for a group of school children. | | From Lewis and Taylor (1967). | *--------------------------------------------------------------*; data htwt; input sex $ age :3.1 height weight @@; datalines; f 143 56.3 85.0 f 155 62.3 105.0 f 153 63.3 108.0 f 161 59.0 92.0 f 191 62.5 112.5 f 171 62.5 112.0 f 185 59.0 104.0 f 142 56.5 69.0 f 160 62.0 94.5 f 140 53.8 68.5 f 139 61.5 104.0 f 178 61.5 103.5 f 157 64.5 123.5 f 149 58.3 93.0 f 143 51.3 50.5 f 145 58.8 89.0 ... more lines ... m 164 66.5 112.0 m 189 65.0 114.0 m 164 61.5 140.0 m 167 62.0 107.5 m 151 59.3 87.0 ;
Modeling is performed separately for boys and girls. Since the BY statement is used, interactive processing is not possible in this example; no statements can appear after the first RUN statement.
The following statements produce Output 76.3.1 through Output 76.3.4:
proc reg outest=est1 outsscp=sscp1 rsquare; by sex; eq1: model weight=height; eq2: model weight=height age; proc print data=sscp1; title2 'SSCP type data set'; proc print data=est1; title2 'EST type data set'; run;
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 1 | 21507 | 21507 | 141.09 | <.0001 |
| Error | 109 | 16615 | 152.42739 | ||
| Corrected Total | 110 | 38121 | |||
| Root MSE | 12.34615 | R-Square | 0.5642 |
|---|---|---|---|
| Dependent Mean | 98.87838 | Adj R-Sq | 0.5602 |
| Coeff Var | 12.48620 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | -153.12891 | 21.24814 | -7.21 | <.0001 |
| height | 1 | 4.16361 | 0.35052 | 11.88 | <.0001 |
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 2 | 22432 | 11216 | 77.21 | <.0001 |
| Error | 108 | 15689 | 145.26700 | ||
| Corrected Total | 110 | 38121 | |||
| Root MSE | 12.05268 | R-Square | 0.5884 |
|---|---|---|---|
| Dependent Mean | 98.87838 | Adj R-Sq | 0.5808 |
| Coeff Var | 12.18939 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | -150.59698 | 20.76730 | -7.25 | <.0001 |
| height | 1 | 3.60378 | 0.40777 | 8.84 | <.0001 |
| age | 1 | 1.90703 | 0.75543 | 2.52 | 0.0130 |
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 1 | 31126 | 31126 | 206.24 | <.0001 |
| Error | 124 | 18714 | 150.92222 | ||
| Corrected Total | 125 | 49840 | |||
| Root MSE | 12.28504 | R-Square | 0.6245 |
|---|---|---|---|
| Dependent Mean | 103.44841 | Adj R-Sq | 0.6215 |
| Coeff Var | 11.87552 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | -125.69807 | 15.99362 | -7.86 | <.0001 |
| height | 1 | 3.68977 | 0.25693 | 14.36 | <.0001 |
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 2 | 32975 | 16487 | 120.24 | <.0001 |
| Error | 123 | 16866 | 137.11922 | ||
| Corrected Total | 125 | 49840 | |||
| Root MSE | 11.70979 | R-Square | 0.6616 |
|---|---|---|---|
| Dependent Mean | 103.44841 | Adj R-Sq | 0.6561 |
| Coeff Var | 11.31945 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | -113.71346 | 15.59021 | -7.29 | <.0001 |
| height | 1 | 2.68075 | 0.36809 | 7.28 | <.0001 |
| age | 1 | 3.08167 | 0.83927 | 3.67 | 0.0004 |
For both female and male children, the overall 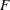 statistics for both models are significant, indicating that the model explains a significant portion of the variation in the data. For females, the full model is
statistics for both models are significant, indicating that the model explains a significant portion of the variation in the data. For females, the full model is
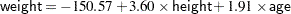 |
and for males, the full model is
 |
The OUTSSCP= data set is shown in Output 76.3.5. Note how the BY groups are separated. Observations with _TYPE_=‘N’ contain the number of observations in the associated BY group. Observations with _TYPE_=‘SSCP’ contain the rows of the uncorrected sums of squares and crossproducts matrix. The observations with _NAME_=‘Intercept’ contain crossproducts for the intercept.
| SSCP type data set |
| Obs | sex | _TYPE_ | _NAME_ | Intercept | height | weight | age |
|---|---|---|---|---|---|---|---|
| 1 | f | SSCP | Intercept | 111.0 | 6718.40 | 10975.50 | 1824.90 |
| 2 | f | SSCP | height | 6718.4 | 407879.32 | 669469.85 | 110818.32 |
| 3 | f | SSCP | weight | 10975.5 | 669469.85 | 1123360.75 | 182444.95 |
| 4 | f | SSCP | age | 1824.9 | 110818.32 | 182444.95 | 30363.81 |
| 5 | f | N | 111.0 | 111.00 | 111.00 | 111.00 | |
| 6 | m | SSCP | Intercept | 126.0 | 7825.00 | 13034.50 | 2072.10 |
| 7 | m | SSCP | height | 7825.0 | 488243.60 | 817919.60 | 129432.57 |
| 8 | m | SSCP | weight | 13034.5 | 817919.60 | 1398238.75 | 217717.45 |
| 9 | m | SSCP | age | 2072.1 | 129432.57 | 217717.45 | 34515.95 |
| 10 | m | N | 126.0 | 126.00 | 126.00 | 126.00 |
The OUTEST= data set is displayed in Output 76.3.6; again, the BY groups are separated. The _MODEL_ column contains the labels for models from the MODEL statements. If no labels are specified, the defaults MODEL1 and MODEL2 would appear as values for _MODEL_. Note that _TYPE_=‘PARMS’ for all observations, indicating that all observations contain parameter estimates. The _DEPVAR_ column displays the dependent variable, and the _RMSE_ column gives the root mean square error for the associated model. The Intercept column gives the estimate for the intercept for the associated model, and variables with the same name as variables in the original data set (height, age) give parameter estimates for those variables. The dependent variable, weight, is shown with a value of 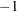 . The _IN_ column contains the number of regressors in the model not including the intercept; _P_ contains the number of parameters in the model; _EDF_ contains the error degrees of freedom; and _RSQ_ contains the
. The _IN_ column contains the number of regressors in the model not including the intercept; _P_ contains the number of parameters in the model; _EDF_ contains the error degrees of freedom; and _RSQ_ contains the  statistic. Finally, note that the _IN_, _P_, _EDF_, and _RSQ_ columns appear in the OUTEST= data set since the RSQUARE option is specified in the PROC REG statement.
statistic. Finally, note that the _IN_, _P_, _EDF_, and _RSQ_ columns appear in the OUTEST= data set since the RSQUARE option is specified in the PROC REG statement.
| EST type data set |
| Obs | sex | _MODEL_ | _TYPE_ | _DEPVAR_ | _RMSE_ | Intercept | height | weight | age | _IN_ | _P_ | _EDF_ | _RSQ_ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | f | eq1 | PARMS | weight | 12.3461 | -153.129 | 4.16361 | -1 | . | 1 | 2 | 109 | 0.56416 |
| 2 | f | eq2 | PARMS | weight | 12.0527 | -150.597 | 3.60378 | -1 | 1.90703 | 2 | 3 | 108 | 0.58845 |
| 3 | m | eq1 | PARMS | weight | 12.2850 | -125.698 | 3.68977 | -1 | . | 1 | 2 | 124 | 0.62451 |
| 4 | m | eq2 | PARMS | weight | 11.7098 | -113.713 | 2.68075 | -1 | 3.08167 | 2 | 3 | 123 | 0.66161 |