The REG Procedure
- Overview
-
Getting Started
-
Syntax
-
Details
Missing Values Input Data Sets Output Data Sets Interactive Analysis Model-Selection Methods Criteria Used in Model-Selection Methods Limitations in Model-Selection Methods Parameter Estimates and Associated Statistics Predicted and Residual Values Models of Less Than Full Rank Collinearity Diagnostics Model Fit and Diagnostic Statistics Influence Statistics Reweighting Observations in an Analysis Testing for Heteroscedasticity Testing for Lack of Fit Multivariate Tests Autocorrelation in Time Series Data Computations for Ridge Regression and IPC Analysis Construction of Q-Q and P-P Plots Computational Methods Computer Resources in Regression Analysis Displayed Output ODS Table Names ODS Graphics
-
Examples
- References
| Models of Less Than Full Rank |
If the model is not full rank, there are an infinite number of least squares solutions for the estimates. PROC REG chooses a nonzero solution for all variables that are linearly independent of previous variables and a zero solution for other variables. This solution corresponds to using a generalized inverse in the normal equations, and the expected values of the estimates are the Hermite normal form of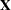 
multiplied by the true parameters:
 |
Degrees of freedom for the zeroed estimates are reported as zero. The hypotheses that are not testable have 
tests reported as missing. The message that the model is not full rank includes a display of the relations that exist in the matrix.
The following statements use the fitness data from Example 76.2. The variable Dif=RunPulse
RestPulse is created. When this variable is included in the model along with RunPulse and RestPulse, there is a linear dependency (or exact collinearity) between the independent variables. Figure 76.34 shows how this problem is diagnosed.
data fit2; set fitness; Dif=RunPulse-RestPulse; proc reg data=fit2; model Oxygen=RunTime Age Weight RunPulse MaxPulse RestPulse Dif; run;
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 6 | 722.54361 | 120.42393 | 22.43 | <.0001 |
| Error | 24 | 128.83794 | 5.36825 | ||
| Corrected Total | 30 | 851.38154 | |||
| Root MSE | 2.31695 | R-Square | 0.8487 |
|---|---|---|---|
| Dependent Mean | 47.37581 | Adj R-Sq | 0.8108 |
| Coeff Var | 4.89057 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | 102.93448 | 12.40326 | 8.30 | <.0001 |
| RunTime | 1 | -2.62865 | 0.38456 | -6.84 | <.0001 |
| Age | 1 | -0.22697 | 0.09984 | -2.27 | 0.0322 |
| Weight | 1 | -0.07418 | 0.05459 | -1.36 | 0.1869 |
| RunPulse | B | -0.36963 | 0.11985 | -3.08 | 0.0051 |
| MaxPulse | 1 | 0.30322 | 0.13650 | 2.22 | 0.0360 |
| RestPulse | B | -0.02153 | 0.06605 | -0.33 | 0.7473 |
| Dif | 0 | 0 | . | . | . |
PROC REG produces a message informing you that the model is less than full rank. Parameters with DF=0 are not estimated, and parameters with DF=B are biased. In addition, the form of the linear dependency among the regressors is displayed.