The MI Procedure
- Overview
- Getting Started
-
Syntax
-
Details
Descriptive Statistics EM Algorithm for Data with Missing Values Statistical Assumptions for Multiple Imputation Missing Data Patterns Imputation Methods Monotone Methods for Data Sets with Monotone Missing Patterns Monotone and FCS Regression Methods Monotone and FCS Predictive Mean Matching Methods Monotone Propensity Score Method Monotone and FCS Discriminant Function Methods Monotone and FCS Logistic Regression Methods FCS Methods for Data Sets with Arbitrary Missing Patterns Checking Convergence in FCS Methods MCMC Method for Arbitrary Missing Multivariate Normal Data Producing Monotone Missingness with the MCMC Method MCMC Method Specifications Checking Convergence in MCMC Input Data Sets Output Data Sets Combining Inferences from Multiply Imputed Data Sets Multiple Imputation Efficiency Imputer’s Model Versus Analyst’s Model Parameter Simulation versus Multiple Imputation Summary of Issues in Multiple Imputation ODS Table Names ODS Graphics
-
Examples
EM Algorithm for MLE Monotone Propensity Score Method Monotone Regression Method Monotone Logistic Regression Method for CLASS Variables Monotone Discriminant Function Method for CLASS Variables FCS Method for Continuous Variables FCS Method for CLASS Variables FCS Method with Trace Plot MCMC Method Producing Monotone Missingness with MCMC Checking Convergence in MCMC Saving and Using Parameters for MCMC Transforming to Normality Multistage Imputation
- References
| Combining Inferences from Multiply Imputed Data Sets |
With 
imputations, different sets of the point and variance estimates for a parameter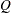 
can be computed. Suppose 
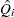and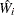 
are the point and variance estimates from the 
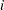th imputed data set, 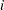= 1, 2, ..., . Then the combined point estimate for 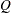from multiple imputation is the average of the complete-data estimates:
 |
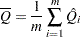Suppose 
is the within-imputation variance, which is the average of the complete-data estimates,
 |
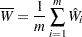and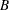 
is the between-imputation variance
 |
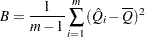Then the variance estimate associated with 
is the total variance (Rubin 1987)
 |
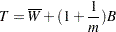The statistic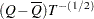 
is approximately distributed as 
with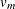 
degrees of freedom (Rubin 1987), where
 |
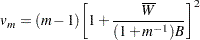The degrees of freedom 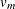depend on and the ratio
 |
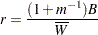The ratio 
is called the relative increase in variance due to nonresponse (Rubin 1987). When there is no missing information about 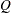, the values of and 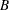are both zero. With a large value of or a small value of , the degrees of freedom 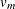will be large and the distribution of 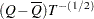will be approximately normal.
Another useful statistic is the fraction of missing information about :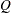
 |
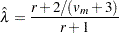Both statistics and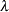 
are helpful diagnostics for assessing how the missing data contribute to the uncertainty about .
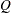When the complete-data degrees of freedom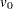 
are small, and there is only a modest proportion of missing data, the computed degrees of freedom, 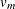, can be much larger than 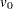, which is inappropriate. For example, with 
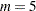and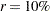 
, the computed degrees of freedom 
, which is inappropriate for data sets with complete-data degrees of freedom less than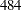 
.
Barnard and Rubin (1999) recommend the use of adjusted degrees of freedom
 |
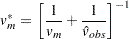where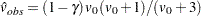 
and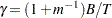 
.
Note that the MI procedure uses the adjusted degrees of freedom,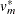 
, for inference.